2. Численное интегрирование: метод прямоугольников

Численное интегрирование (историческое название: квадратура) - вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади криволинейной трапеции, ограниченной осью абсцисс, графиком интегрируемой функции и отрезками прямых и , где и - пределы интегрирования.

Необходимость применения численного интегрирования чаще всего может быть вызвана отсутствием у первообразной функции представления в элементарных функциях. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом [1].

2.1. Квадратурные формулы.

Постановка задачи численного интегрирования.

Пусть требуется вычислить

(1)

Если - первообразная для , то . Часто получить выражение для первообразной не удается. Подынтегральная функция может быть задана в табличном виде. В этих случаях подынтегральную функцию заменяют на некоторую аппроксимирующую функцию, интеграл от которой легко вычисляется в элементарных функциях. Для аппроксимации подынтегральной функции часто используют интерполяцию. Во многих случаях формулы для приближенного вычисления интегралов (1) можно записать в виде

(2)

Формулы такого вида называются квадратурными.

- узлы квадратурной формулы.

- коэффициенты.

- погрешность (остаточный член ) квадратурной формулы [7].

Сумма в правой части формулы (2) называется квадратурной суммой.

Квадратурная формула называется интерполяционной, если

(3)

Важной характеристикой квадратурной формулы является ее алгебраическая степень точности.

Определение: целое неотрицательное число d называется алгебраической степенью точности квадратурной формулы, если эта формула точна для всех многочленов степени не выше d и не точна для x^d+1.

Теорема:

Для того чтобы квадратурная формула с n попарно различными узлами была интерполяционной, необходимо и достаточно, чтобы d³n-1 [5].

2.2. Квадратурные формулы прямоугольников.

Построение.

Простейшая квадратурная формула получается при использовании интерполяционного многочлена нулевой степени.

Фиксируем и заменяем подинтегральную функцию интерполяционным многочленом нулевой степени, который совпадает со значением : . Тогда

(4)

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс [6].

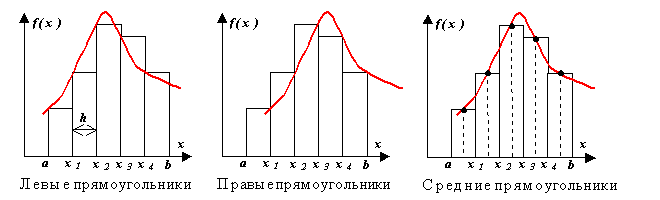
Частные случаи:

- формула левых прямоугольников

- формула правых прямоугольников

- формула средних прямоугольников.

Квадратурные формулы прямоугольников

Квадратурная формула левых прямоугольников:

Очевидно, что ее алгебраическая степень точности d=0 и формула является интерполяционной.

Квадратурная формула правых прямоугольников

Квадратурная формула средних прямоугольников

Алгебраическая степень точности d=1 и формула является интерполяционной [5].

Составные квадратурные формулы прямоугольников

Разбиваем промежуток интегрирования [a,b] на N равных частей, h=(b-a) N — длина частичного разбиения.

Обозначим , . Составные квадратурные формулы прямоугольников напишем в следующем виде:

(5)

где при g=a получаем формулу левых прямоугольников, при g=a+h/2 — средних прямоугольников, при g=a+h — правых прямоугольников.

Обратим внимание, что алгебраические степени точности формул остаются прежними и составные квадратурные формулы не являются интерполяционными[5].

Оценка погрешности.

Пусть существует , непрерывная на . По формуле Тейлора: . Интегрируя, получаем:

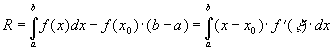(6)

Обозначим .

Используем вариант теоремы о среднем, который имеет вид: если непрерывна и - интегрируема, то

,

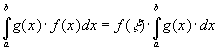где .

Пусть . Имеем .

(7)

Пусть . Имеем и оценка для будет того же вида (6).

Таким образом, (6) - оценка погрешности формул правых и левых прямоугольников.

Оценим погрешность для формулы средних прямоугольников.

Пусть существует . По формуле Тейлора имеем:

.

Интегрируя, получаем

Так как, , то

. Отсюда следует оценка

(8)

Для повышения точности квадратурных формул можно промежуток разбить точками , , на частичные промежутки, к каждому из которых применяется формула прямоугольников

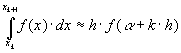, , (9)

Суммируя по , получаем обобщенную формулу прямоугольников.

(10)

при - формула левых прямоугольников,

при - формула правых прямоугольников,

при - формула средних прямоугольников.

Оценка остаточного члена для обобщенной формулы получается на основе оценок (6) или (7) соответственно.

При , :

(11)

При :

(12)

Из оценок (11) и (12) следует, что выбирая достаточно большое число точек разбиения (т.е. делая достаточно малым) можно получить результат с необходимой точностью [7].