5.3 Численное интегрирование дифференциальных уравнений в

расчетах динамической устойчивости

Расчет динамической устойчивости может производиться любым методом численного интегрирования. При расчетах на ЭВМ обычно используется для этих целей явный метод типа Рунге-Кутта четвертой степени [9], имеющийся в математическом обеспечении практически всех ЭВМ.

В курсовой работе для численного интегрирования дифференциального уравнения (5.1) без использования ЭВМ используется метод после–довательных интервалов. Для расчета зависимостей и переходный процесс разбивается на малые ( ) отрезки времени, на протяжении которых ускорение считается неизменным. При решении уравнения (5.1) порядок расчета следующий:

1. По разности мощностей первичного двигателя (турбины) и генератора

для начала процесса определяется изменение угла за первый расчетный интервал

, (5.7)

где ;

и находится значение угла в конце первого интервала

, где . (5.8)

2. По новому значению угла определяется разность мощностей в начале второго интервала и находится приращение угла за второй интервал

, (5.9)

где ,

а затем новое значение угла .

3. Для приращений угла во всех последующих интервалах используется

формула

. (5.10)

При скачкообразных изменениях режима в течение переходного процесса (изменения вида КЗ, отключение КЗ успешное АПВ – автоматическое пов–торное включение), когда избыток мощности внезапно изменяется от до , приращение угла интервала находится из выражения . (5.11)

Расчет производится либо до начала уменьшения угла , что свидетельствует о сохранении устойчивости, либо до предельного по условиям устойчивости угла . Расчеты удобно вести в табличной форме. По результатам расчета строятся зависимости и с обозначением хара–ктерных углов и значений времени. В случае отсутствия динамической устой–чивости определяется предельный угол и время отключения КЗ (см. главу 5.3).

При учете реакции якоря и действия регуляторов возбуждения совместно с уравнением движения методом Эйлера [9] решаются дифференциальные уравнения (5.4) с учетом соотношения (5.5). Расчет производится в следующем порядке [2, 3]:

1. В исходном режиме определяются значения начального угла 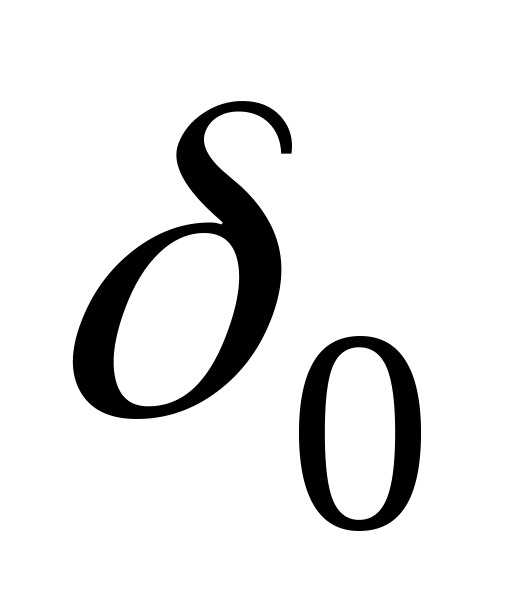, эдс

, и среднее значение за расчетный интервал времени.

2. Определяются взаимные реактивности 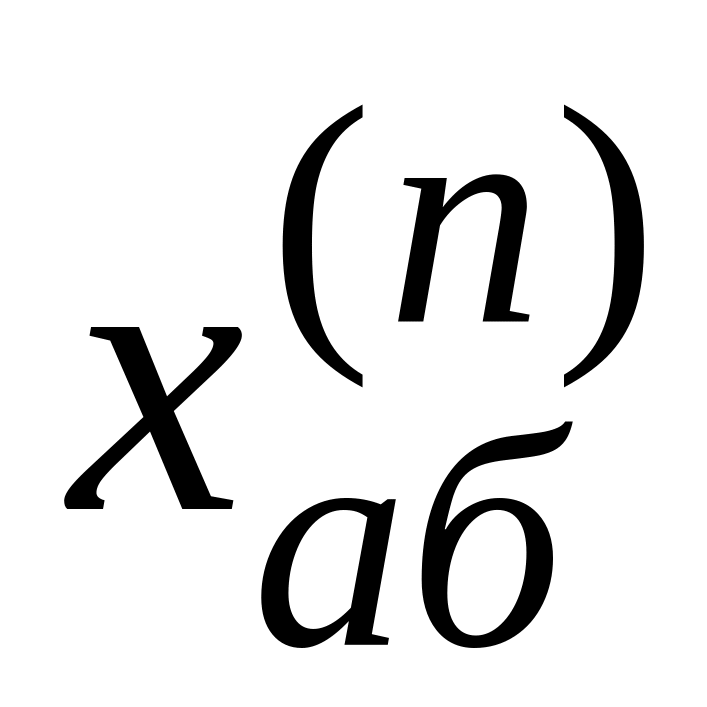для всех расчетных

ситуаций, при этом генератор вводится в схему замещения сопротивлением .

3. По выражению (5.6), с учетом замечаний для явнополюсной машины

определяется эдс холостого хода для первого момента нарушения режима – .

4. Находится изменение переходной эдс в течение первого расчетного

интервала

, (5.12)

и значение переходной эдс в конце первого интервала

. (5.13)

5. Определяется активная мощность генератора в начале первого интервала

(5.14)

и небаланс мощности .

6. По выражениям метода последовательных интервалов (5.7), (5.8)

находятся приращения угла и угол в начале следующего интервала.

7. В результате этого расчета определены значения 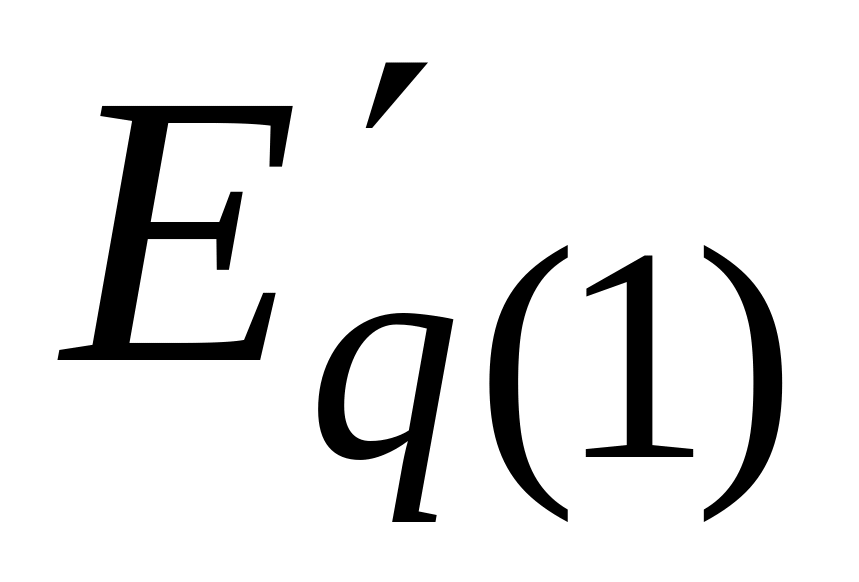и в начале

второго интервала, по которым находится величина эдс и повторяется расчет для нового интервала.

По результатам расчетов строится зависимость во времени угла , эдс ,

, и делаются выводы о характере их изменения.

Пример 5 – Численный расчет динамического перехода

Первый шаг численного расчета динамического перехода.

Частота , ,

Гц/с,

с, ,

,

, ,

,

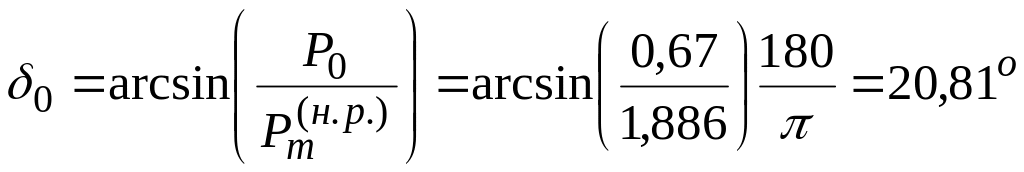и т.д.

При скачкообразных изменениях режима в течение переходного процесса избыток мощности внезапно изменяется от до . В момент перехода от к :

где

Результаты расчетов, согласно формулам, представленным выше, сведены в табл. 5.2 и построены зависимости – рис. 5.8 и – рис. 5.9 .

Из результатов расчета и из графика рис. 5.8 видно, что устойчивость сохраняется, так как, начиная с t=0,475 c угол δ начинает уменьшаться.

Таблица 5.2 – Результаты расчета динамического перехода

t, c	, град	, град/с.	град	, о. е
0	20,81	–	–
0,025	21,06	812,10	0,25
0,05	21,82	804,00	0,76
0,075	23,06	779,95	1,24
0,1	24,77	740,68	1,71
0,125	26,91	687,38	2,14
0,15	29,43	621,69	2,52
0,175	32,30	545,65	2,87
0,2	35,60	950,90	3,31
0,225	39,47	901,02	3,87
0,25	43,87	845,23	4,40
0,275	48,76	785,51	4,89
0,3	54,10	724,12	5,34
0,325	59,86	663,59	5,76
0,35	66,00	606,58	6,14
0,375	72,48	555,83	6,48
0,4	78,42	-2247,37	5,94
0,425	82,90	-2379,89	4,47
0,45	85,87	-2399,77	2,97
0,475	87,33	-2419,77	1,46
0,5	87,27	-2425,73	-0,06

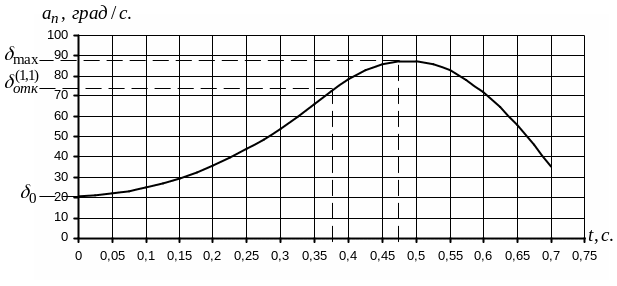
Рисунок 5.8 – Зависимость угла рассогласования, от времени

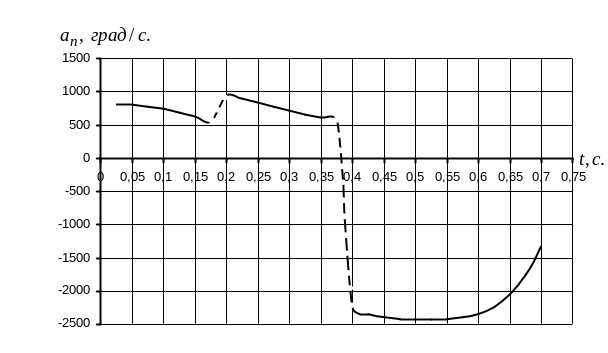Рисунок 5.9 – Зависимость ускорения от времени