МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Машиноведение и сертификация

транспортной техники»

В.Д. ГВОЗДЕВ

Универсальные средства измерений

Рекомендовано редакционно-издательским советом

университета в качестве учебного пособия

по дисциплине «Метрология, стандартизация и сертификация»

для студентов специальностей

190205 – «Подъемно-транспортные, строительные, дорожные машины и оборудование»,

190702 – «Организация и безопасность движения (железнодорожный транспорт)»,

190302 – «Вагоны»

Москва - 2008

УДК 531.7:389

Г-25

Гвоздев В.Д. Универсальные средства измерений. Учебное пособие - М.: МИИТ, 2008. – 108 с.

Рассматриваются средства и методы измерений линейных и угловых размеров. Приведены справочные материалы, позволяющие осуществлять выбор средств измерений и контроль качества объектов измерений.

Рецензенты: к.т.н. Мицкевич В.Г.

РГОТУПС

к.т.н. Фомин В.И.

МИИТ

© Московский государственный университет путей сообщения

(МИИТ), 2008

_______________________________________________________

Св. план 2008 г., поз.

Гвоздев Владимир Дмитриевич

Универсальные средства измерений

Учебное пособие

Подписано к печати - Формат 60х84/16.

Усл. – п.л. - 6,75 Заказ № Тираж

127994 Москва, ул. Образцова, 15. Типография миит

Лабораторная работа № 1

Анализ заданной посадки.

Цель работы: Знакомство со стандартами Единой системы допусков и посадок (ЕСДП), усвоение их назначения и порядка применения.

Исходные положения. Значение размера детали, получаемое в результате ее изготовления, вследствие влияния различных факторов (температурные и силовые деформации, погрешности технологического оборудования, неоднородность свойств материалов и другие факторы), является случайной величиной. Вероятность получения конкретного заданного значения размера равна нулю. В этой связи, для обеспечения экономичности изготовления конструктор в технической документации задает диапазон допустимых значений для каждого размера детали, исходя из условия обеспечения качества детали и изделия, в которое входит деталь, в целом (например, вместо расчетного значения 32 мм записывают диапазон 31,9 мм – 32,1 мм). Максимальное значение размера в указанном диапазоне называют наибольшим предельным размером (обозначим Amax), минимальное значение – наименьшим предельным размером (Amin). Разность между наибольшим и наименьшим предельными размерами называют допуском размера – TA

TA = Amax – Amin. (1)

Диапазон размеров, ограниченный наибольшим и наименьшим предельными размерами, называют полем допуска.

При изготовлении детали предельные размеры используют для определения ее годности. Деталь признается годной, если ее действительный размер находится между предельными размерами или равен одному из них. (Действительным размером называют размер, полученный измерением с допустимой погрешностью, т.е. погрешность измерения, представляемая как сумма погрешностей средства и метода измерений, субъективной погрешности и погрешности вследствие отличия условий измерения от нормальных, не должна превышать допустимую погрешность измерений. Допустимая погрешность измерений устанавливается стандартами или другими документами и, как правило, не превышает 0,3 ТА.)

В технической документации предельные размеры задают указанием номинального размера А и предельных отклонений: верхнего отклонения Es(A) и нижнего отклонения Ei(A). При этом номинальным размером называют размер, относительно которого определяют предельные отклонения.

Верхним отклонением называют разность между наибольшим предельным размером и номинальным размером

Es(A) = Amax – A (2)

Нижним отклонением называют разность между наименьшим предельным размером и номинальным

Ei(A) = Amin – A (3)

При известных предельных отклонениях допуск размера может быть вычислен по формуле

TA = Amax – Amin = Es(A) – Ei(A) (4)

Таким образом, например, вместо предельных размеров Amax = 58,06 мм и Amin = 58,02 мм на чертеже указывают , где 58 мм – номинальный размер А, +0,06 мм – верхнее отклонение Es(A), +0,02 мм – нижнее отклонение Ei(A). Если в качестве номинального размера принять А = 58,03 мм, то получим ES(A) = +0,03 мм, Ei(A) = -0,01 мм и обозначение предельных размеров . Отсюда следует, что значения предельных отклонений зависят от выбора номинального размера. Как правило, номинальный размер выбирают из ряда нормальных линейных размеров по стандарту ГОСТ 6636.

Величина допуска не зависит от значения номинального размера и равна

ТА = 0,06 – 0,02 = 0,03 – (-0,01) = 0,04 мм.

Графическое представление предельных размеров называют схемой поля допуска. Построение ведут в произвольно выбранном масштабе, располагая числовую ось вертикально (рисунок 1.1.а). Проводят линии, соответствующие предельным размерам, и пространство между ними произвольно ограничивают справа и слева. Полученный прямоугольник и является, собственно, полем допуска.

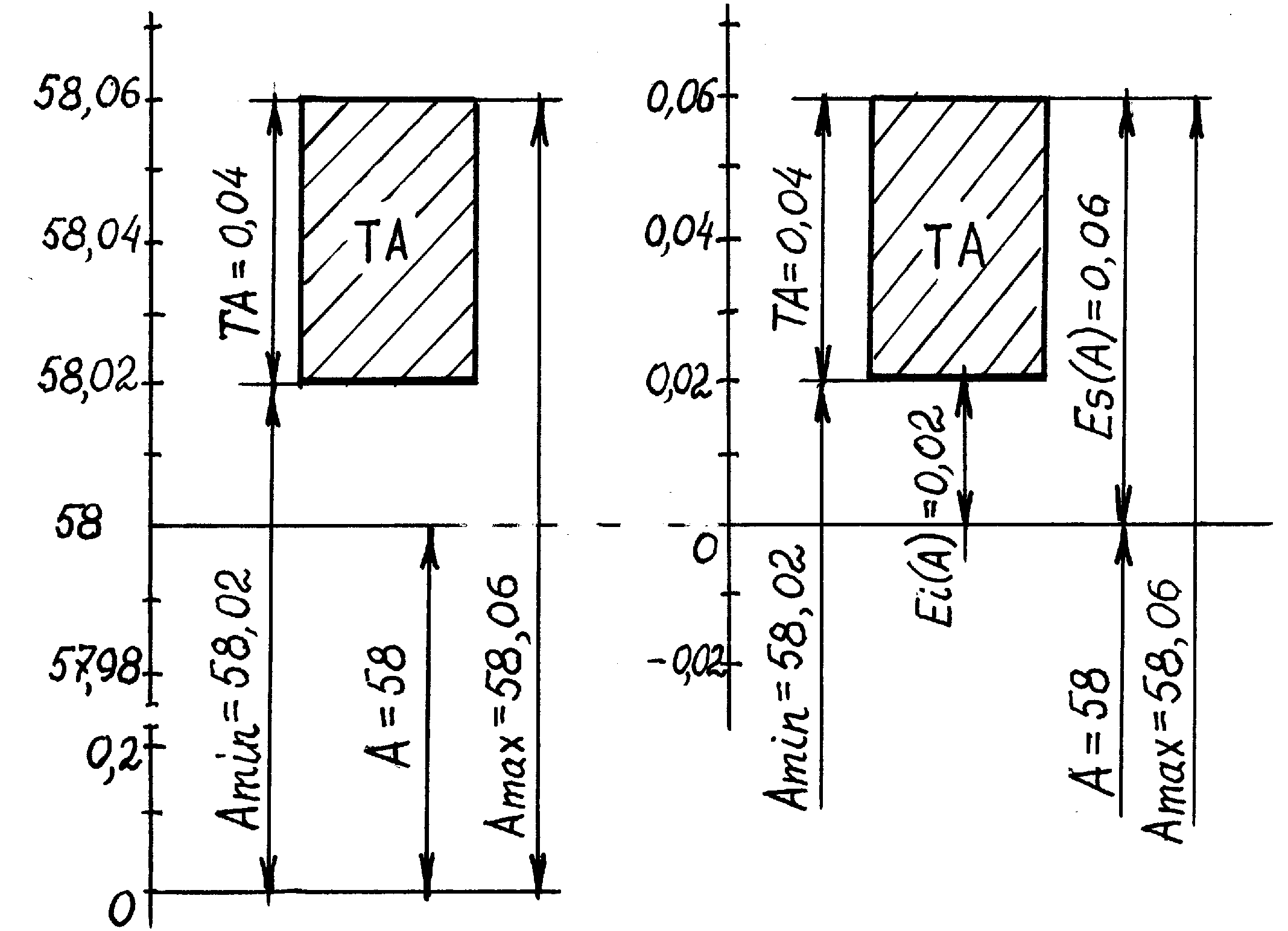
а) б)

Рис.1.1. Схема поля допуска: а) – в абсолютных координатах;

б) – в относительных координатах.

В относительных координатах (рис.1.1.б), когда за нуль принимают значение номинального размера, а числовая ось воспроизводит значения отклонений от номинального размера, границы поля допуска определяются значениями предельных отклонений. На практике используют вариант схемы поля допуска, показанный на рисунке 1.1.б.

Форма детали определяется сочетанием наружных и внутренних поверхностей (внутренние поверхности могут отсутствовать), которые в соединениях с другими деталями выступают как охватываемые и охватывающие поверхности. Во взаимозаменяемости охватывающие (внутренние) поверхности называют отверстиями, а охватываемые (наружные) – валами.

При нормировании предельных отклонений, как и в случае с номинальным размером, конструктор руководствуется требованиями нормативных документов. Применительно к размерам плоских параллельных и гладких цилиндрических поверхностей обрабатываемых резанием, такими документами являются стандарты Единой системы допусков и посадок (ЕСДП).

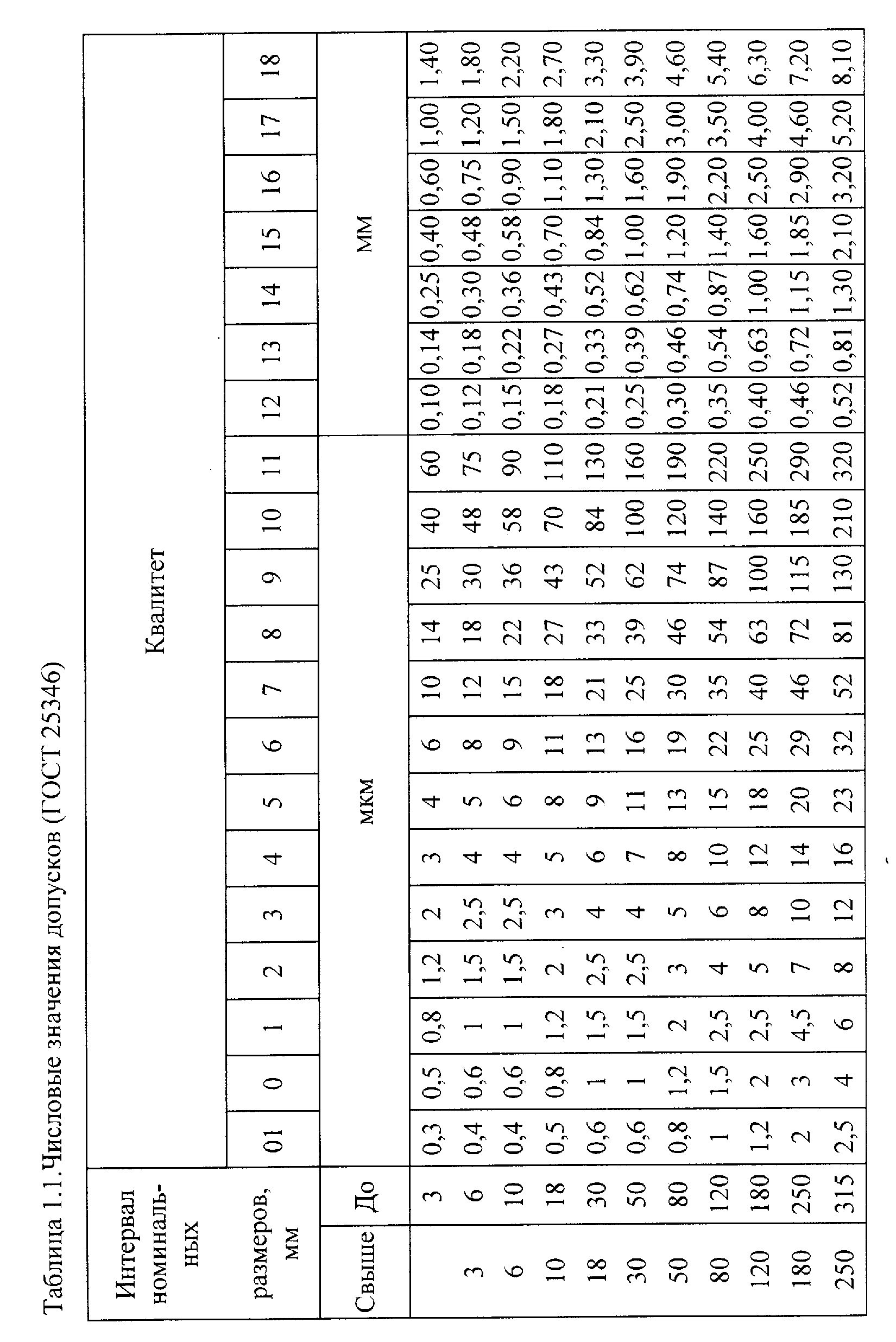
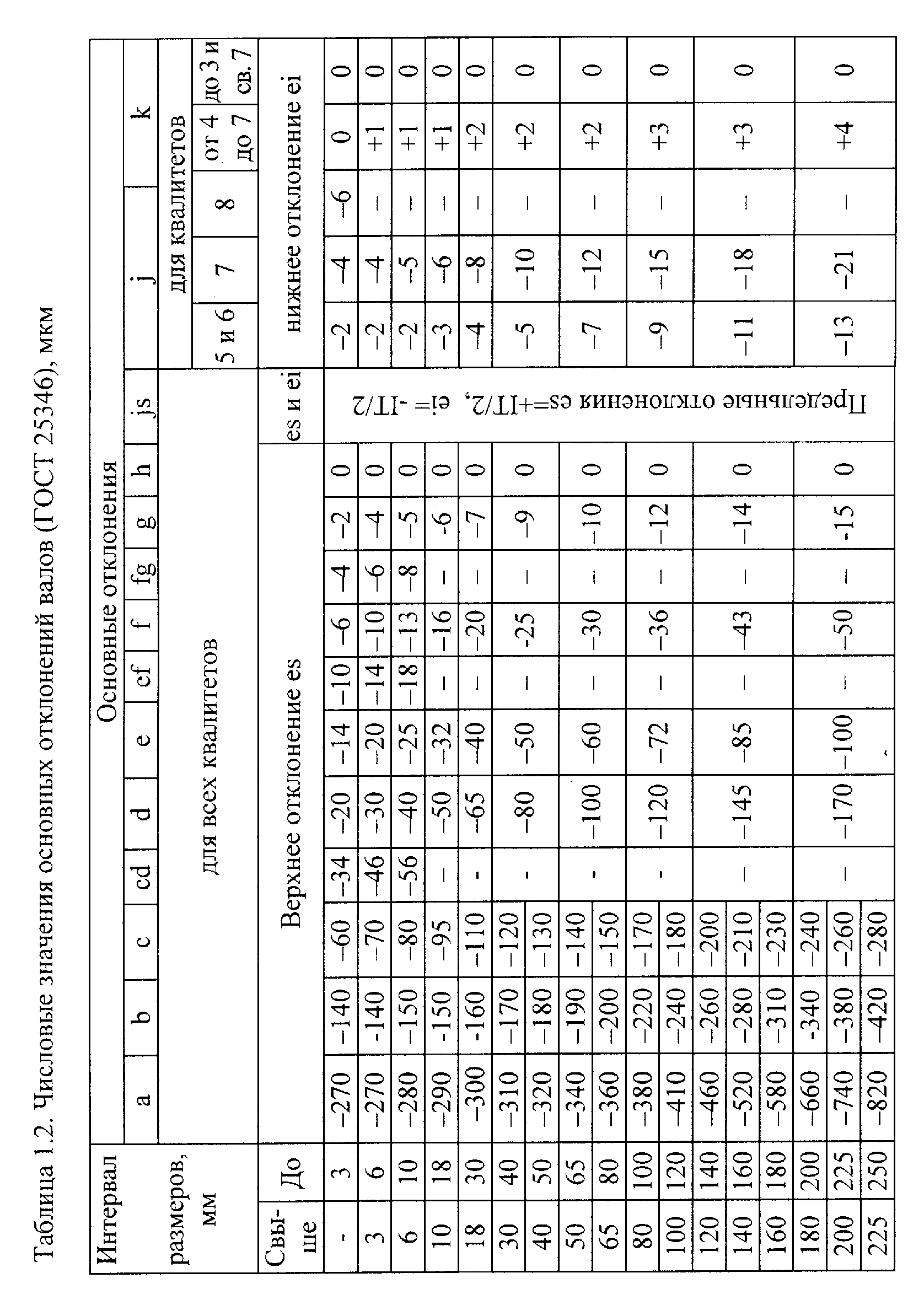
Основу ЕСДП составляют ряды допусков, называемые квалитетами, и ряды основных отклонений. (Основным отклонением называется одно из предельных отклонений, верхнее или нижнее, ближайшее к нулевой линии или, то же самое, меньшее по абсолютной величине). Квалитеты (ряды допусков) нумеруют цифрами от 01 до 18 (таблица 1.1). Ряды основных отклонений обозначают прописными буквами латинского алфавита ( от А до ZC) для отверстий и строчными буквами (от a до zc) для валов (таблицы 1.2 и 1.3). Значения допусков и основных отклонений в таблицах приведены в микрометрах – мкм (1 мкм = 0,001 мм). В ЕСДП номинальный размер отверстия обозначают D, предельные размеры – Dmax и Dmin, верхнее отклонение - ES, нижнее отклонение – EI, допуск - TD. Для валов, соответственно, используют обозначения d, dmax, dmin, es, ei, Td.

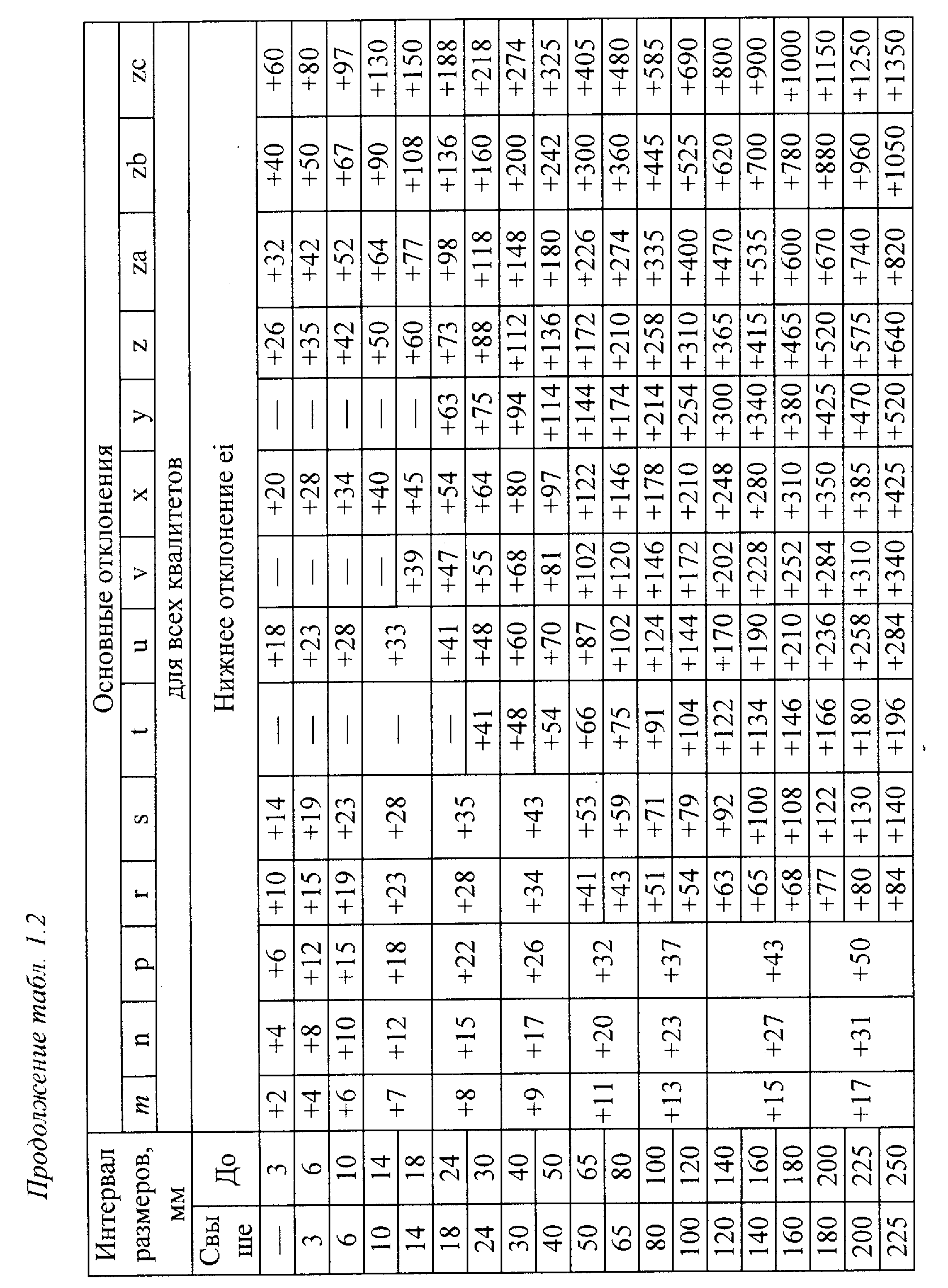
Используя обозначения рядов, предельные размеры можно задавать в условном виде, например, 63f8, где 63 мм – номинальный размер вала (так как буква f строчная), f – обозначения ряда основных отклонений, 8 – номер квалитета (ряда допусков). Для того чтобы найти предельные отклонения вала, выполним следующие действия. Из таблицы допусков (табл.1.1) для интервала размеров от 50 до 80 мм (у нас 63 мм) из столбца под номером 8 (номер квалитета) находим значение допуска Td = IT8 = 45 мкм = 0,045 мм. В таблице основных отклонений валов (табл.1.2) находим ряд f и в строке под ним читаем «верхнее отклонение es». То есть в данном случае в таблице приведено основное отклонение, которое является верхним отклонением. Значение основного отклонения найдем на пересечении столбца f и строки, соответствующей интервалу размеров св. 50 до 80 мм. Записываем es = - 30 мкм = - 0,030 мм. Второе предельное отклонение (в данном случае нижнее отклонение) вычисляем, используя формулу (4):

ei = es – Td = - 0,030 – 0,045 = - 0,075 мм.

Решение задачи 63f8 = позволяет вычислить предельные размеры по формулам (2) и (3):

dmax = d +es = 63 + (-0,030) = 62,970 мм,

dmin = d +ei = 63 + (-0,075) = 62,925 мм.

Анализируя таблицы основных отклонений отверстий и валов, особо отметим ряды, обозначенные буквами H и h, для которых, соответственно, EI = 0 и es = 0. Во взаимозаменяемости вал, у которого верхнее отклонение равно нулю, называется основным валом, отверстие, у которого нижнее отклонение равно нулю, называется основным отверстием. Поэтому обозначения предельных размеров отверстия, например, 70Н8, 32 Н12, 120Н9 и т.д., определяют основное отверстие (EI = 0), а обозначения 50h7, 68h6, 240h11 и т.д. указывают на то, что вал является основным (es = 0).

В машинах и механизмах детали соединяются друг с другом, образуя сопряжения. По определению, сопряжение – подвижное или неподвижное соединение двух или нескольких деталей. Поверхности, по которым осуществляется взаимодействие деталей в сопряжении, называют сопрягаемыми поверхностями, остальные поверхности называют свободными.

В простейшем случае речь идет о соединении двух деталей. Как было отмечено ранее, охватывающую поверхность в сопряжении называют отверстием, а охватываемую поверхность называют валом.

В зависимости от соотношения действительных размеров вала и отверстия перед сборкой различают соединения с зазором и соединения с натягом. Если диаметр отверстия больше диаметра вала, то разность - = называется зазором, и в результате сборки получаем соединение с зазором. Если диаметр вала больше диаметра отверстия, то разность - = называется натягом, и в результате сборки получаем соединение с натягом. Соединения с зазором – подвижные соединения. Соединения с натягом – неподвижные соединения, способные без дополнительных соединительных деталей передавать нагрузку, определяемую значением натяга.

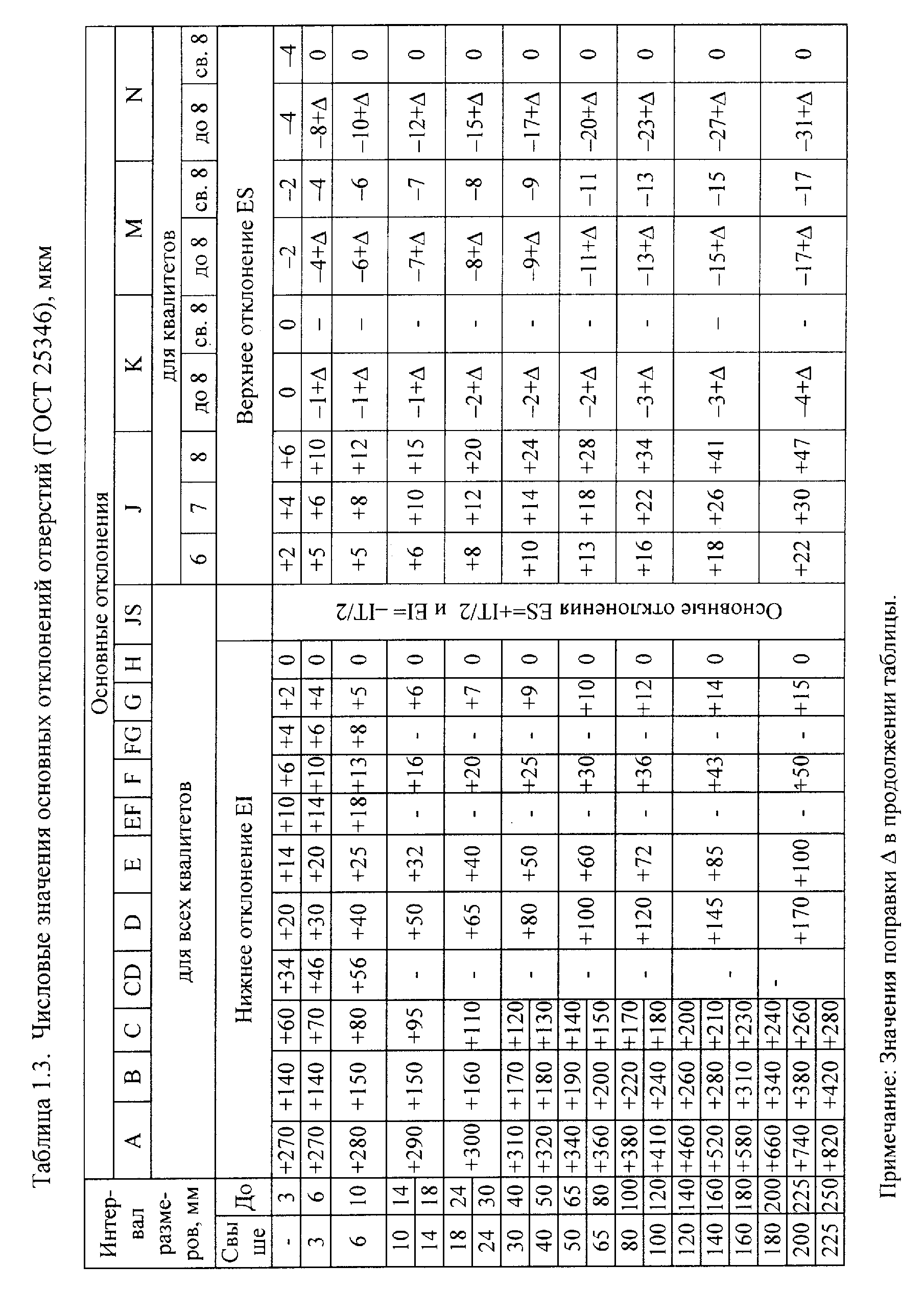
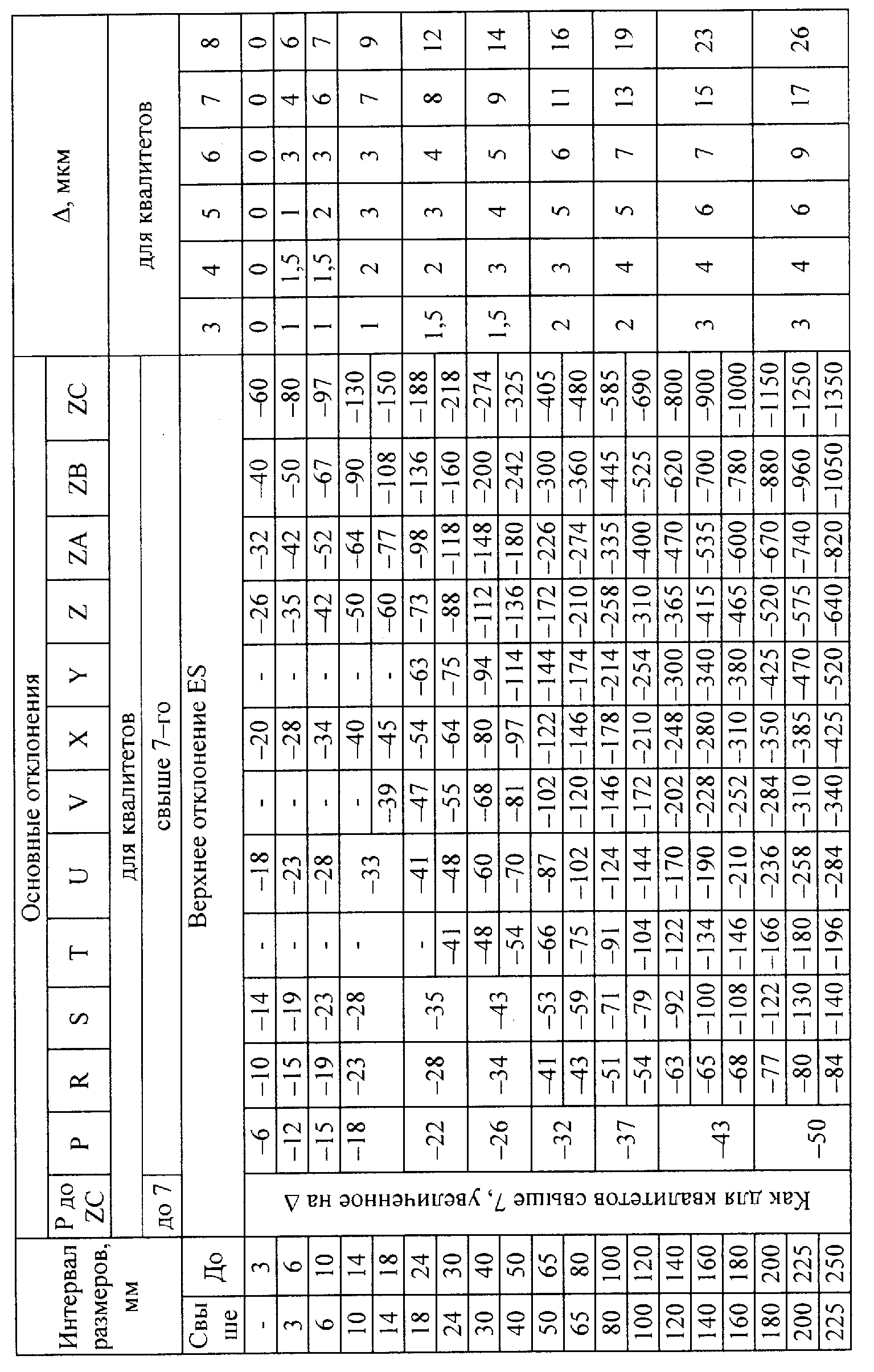
Возможность получения при сборке зазоров и натягов (характер/вид сопряжения) и их числовые значения (характеристики сопряжения) устанавсивает конструктор, задавая предельные размеры сопрягаемых поверхностей. Заданный характер сопряжения, определяемый возможностью получения при сборке зазоров и/или натягов, называется посадкой. Если при сборке могут быть получены только соединения с натягом, говорят, что задана посадка с натягом. Если предельные размеры сопрягаемых поверхностей заданы так, что при сборке могут быть получены только соединения с зазором, говорят, что задана посадка с зазором. Если при сборке возможно получение как соединений с зазором, так и соединений с натягом, то говорят, что задана переходная посадка. Перечисленные ситуации проиллюстрированы с помощью схем полей допусков, показанных на рисунке 1.2.

В первом варианте (рис. 1.2.а) поле допуска вала располагается выше поля допуска отверстия. Соотношение размеров dmin > Dmax означает, что для данного сопряжения действительный размер годного вала при сборке всегда будет больше действительного размера годного отверстия (в качестве напоминания: годной считается деталь, действительный размер которой не выходит за границы поля допуска). В соединении возможен только натяг (задана посадка с натягом), предельные значения которого равны

максимальный натяг Nmax = dmax – Dmin = es – EI (5)

минимальный натяг Nmin = dmin – Dmax = ei – ES (6)

Во втором варианте (рис. 1.2.б) поле допуска отверстия располагается выше поля допуска вала. Соотношение размеров Dmin > dmax означает, что для данного сопряжения действительный размер годного отверстия при сборке всегда будет больше действительного размера годного вала. В соединении возможен только зазор (задана посадка с зазором). Предельные значения зазора:

максимальный зазор Smax = Dmax– dmin = ES – ei (7)

минимальный зазор Smin = Dmin – dmax = EI – es (8)

а)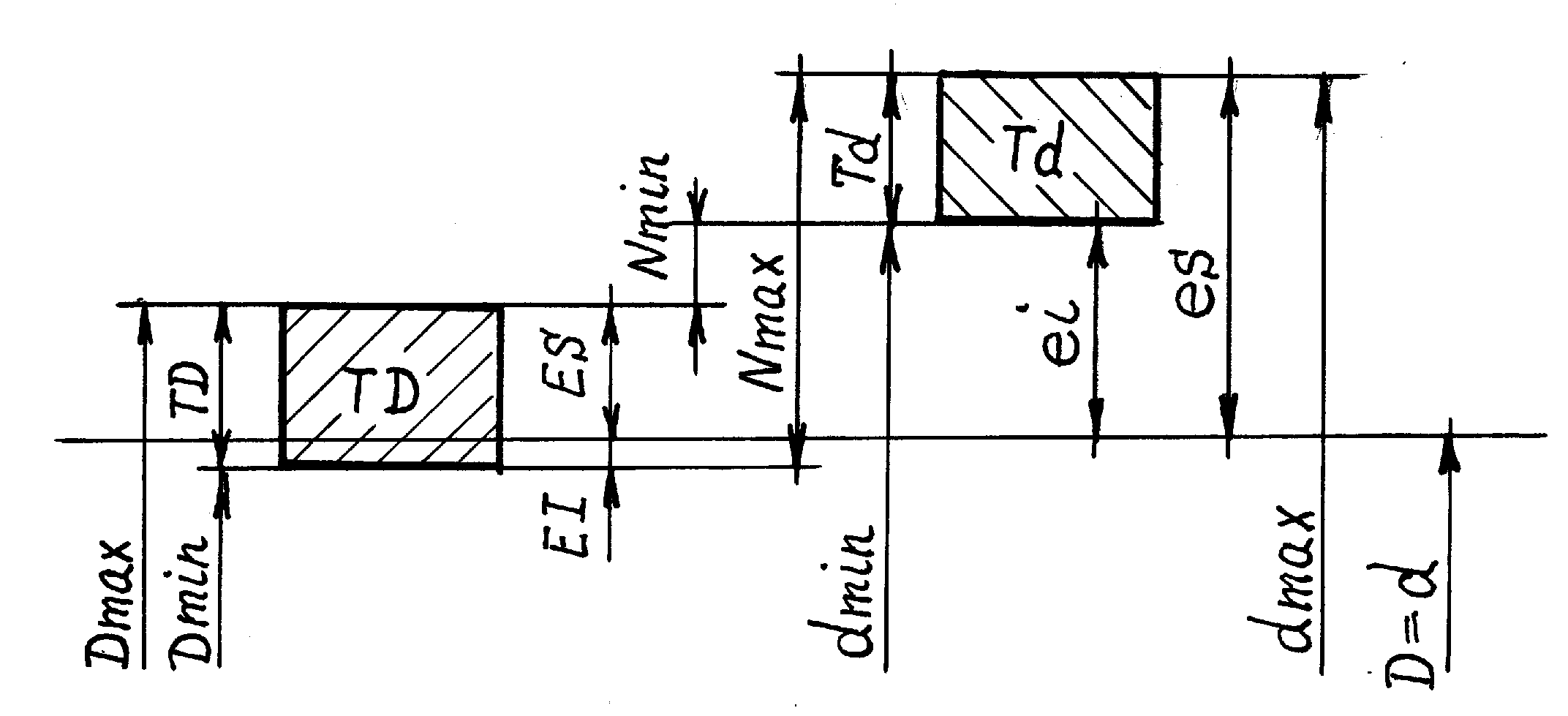

б)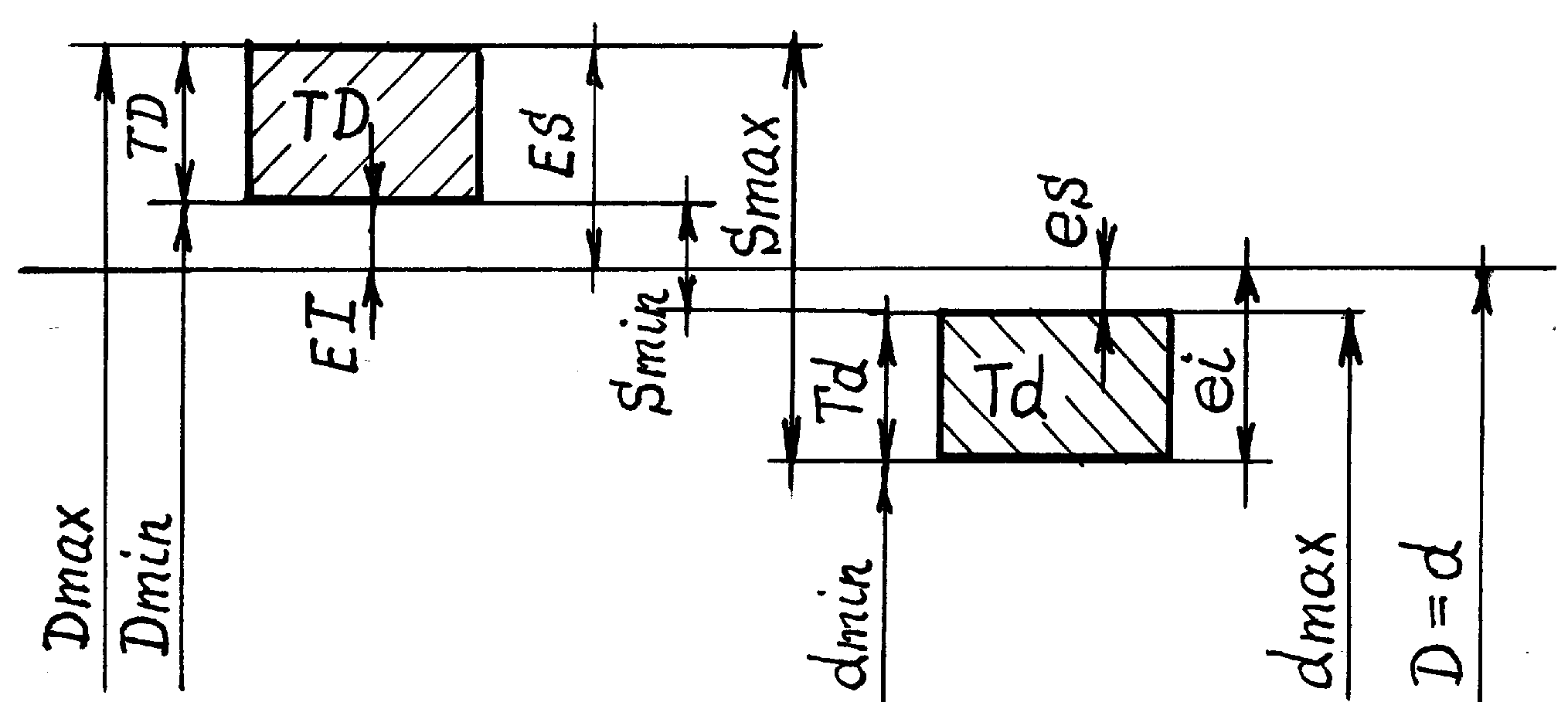

в)

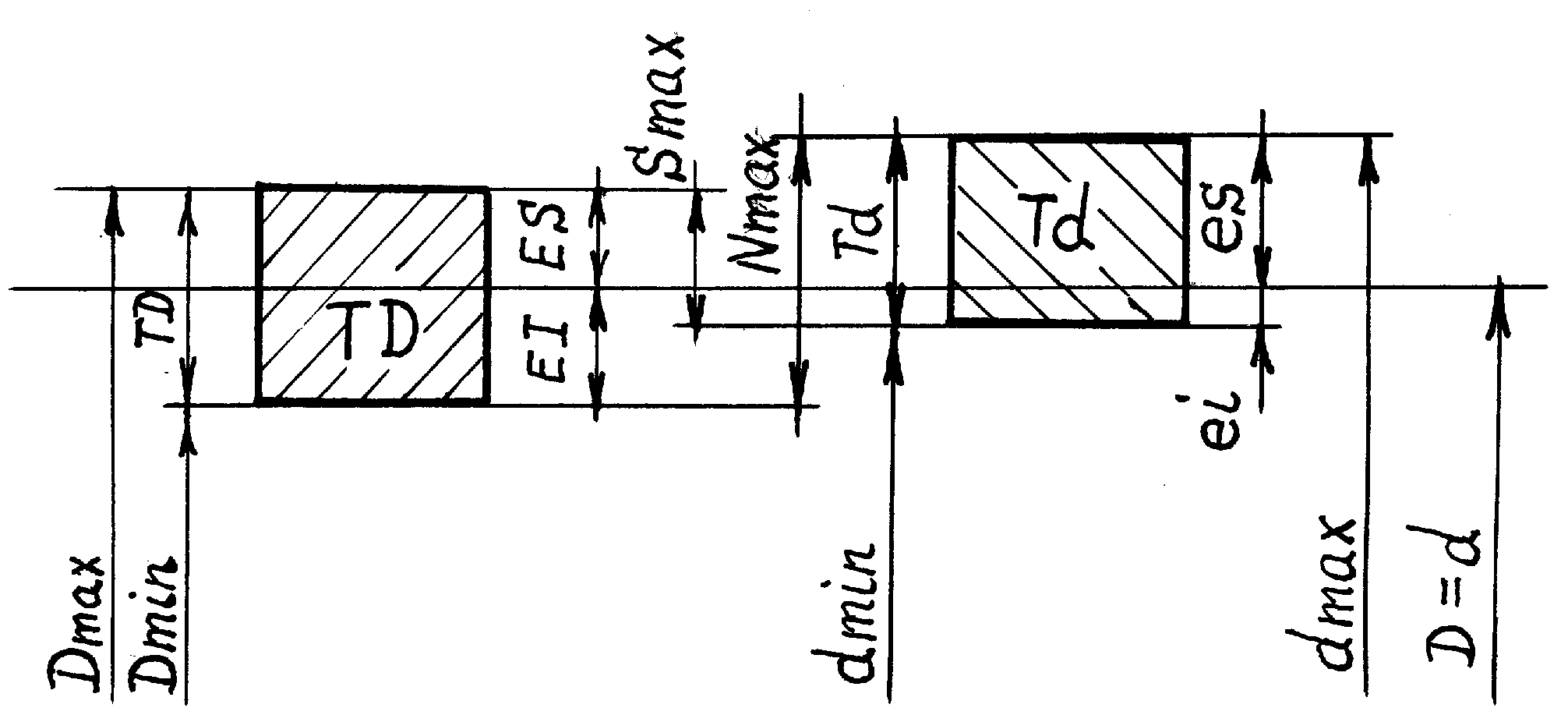
Рис.1.2. Схемы полей допусков: а) посадка с натягом;

б) посадка с зазором; в) переходная посадка.

В варианте, показанном на рисунке 1.2.в, при перемещении изображения любого из полей допусков вдоль линии номинального размера изображения полей допусков налагаются друг на друга, диапазоны предельных размеров вала и отверстия перекрываются (ни одно из условий dmin > Dmax и Dmin > dmax не выполняется), при сборке возможен как зазор, так и натяг:

максимальный натяг Nmax = dmax – Dmin = es – EI (9)

максимальный зазор Smax = Dmax– dmin = ES – ei (10)

Значения зазоров и натягов, вычисленные через предельные размеры (отклонения), также являются наибольшими и наименьшими предельными размерами. В соответствии с определением допуска как разности между предельными размерами запишем:

допуск посадки с натягом

TN = Nmax - Nmin = dmax – Dmin – (dmin – Dmax) =

= dmax – dmin+ Dmax – Dmin = Td + TD ; (11)

допуск посадки c зазором

ТS = Smax - Smin = Dmax– dmin –(Dmin – dmax) =

= Dmax – Dmin+ dmax – dmin = TD + Td ; (12)

допуск переходной посадки (для вычисления используем формулу (11), представляя минимальный зазор как максимальный натяг со знаком минус Smin= - Nmax)

TS(N)= Smax – Smin= Smax+ Nmax=

=Dmax– dmin+ dmax – Dmin= TD + Td . (13)

Предельные размеры отверстия и вала, образующих сопряжение, на чертежах общего вида и в технической документации указываются в виде

Ø или Ø

или Ø или Ø

и называют обозначением посадки.

В приведенных обозначениях:

90 – номинальный размер сопряжения, одинаковый для вала и отверстия;

Ø90Н8 и Ø90k7 – обозначения предельных размеров отверстия и вала, соответственно;

Н8 и k7 – условное обозначение предельных отклонений (полей допусков) отверстия и вала;

Н и k - буквенное обозначение рядов основных отклонений отверстия и вала;

8 и 7 - номера квалитетов (рядов допусков);

+0,054 – верхнее отклонение – ES отверстия (отклонение, равное нулю, в данном случае EI = 0 , не указывают);

+0,038 – верхнее отклонение вала – es;

+0,003 – нижнее отклонение вала – ei.

В зависимости от принципа образования посадок различают посадки в системе отверстия, в системе вала и внесистемные.

Системой отверстия называют совокупность посадок, образованных сочетанием полей допусков основных отверстий с различными валами.

Системой вала называют совокупность посадок, образованных сочетанием полей допусков основных валов с различными отверстиями.

Среди посадок 1) Ø70H7/k6, 2) 40H7/s5, 3) Ø48F7/h6, 4) 38JS9/h9, 5) 7D9/f8, 6) 56A11/g10 первая и вторая посадки заданы в системе отверстия (отверстие основное, т.к. основное отклонение Н, для которого EI =0). Третья и четвертая посадки заданы в системе вала (вал основной, т.к. основное отклонение h, для которого es =0). Пятая и шестая посадки – внесистемные (не относятся ни к системе отверстия, ни к системе вала).

Порядок выполнения работы

1.Ознакомиться с содержанием таблиц Единой системы допусков и посадок.

2.По заданному обозначению посадки:

-определить допуски, предельные отклонения и предельные размеры отверстия и вала;

-построить схему полей допусков отверстия и вала;

-установить вид посадки и систему посадок, к которой она относится;

-вычислить предельные значения зазоров и/или натягов и допуск посадки.

Рассмотрим последовательность действий на примере.

Задача. Выполнить анализ посадки Ø52M8/js7. (Курсивом оформлены записи, которые необходимо привести в тетради лабораторных работ)

1.Определяем предельные отклонения отверстия Ø52M8.

В обозначении поля допуска отверстия задан квалитет 8. Находим значение допуска. В таблице 1.1 на пересечении строки интервала размеров от 50 до 80 мм (левый столбец) и столбца (квалитета) №8 указано значение допуска 45 мкм.

Записываем:

Допуск отверстия TD = IT8 = 45 мкм =0,045 мм

В обозначении поля допуска указан ряд основных отклонений М. В таблице основных отклонений отверстий – табл.1.3 находим ряд, обозначенный М и над ним читаем: «верхнее отклонение ES». На пересечении столбца М для квалитета до 8 и строки с интервалом размеров от 50 до 80 находим значение основного отклонения -11+ . Значение поправки находим с правой стороны таблицы в столбце 8 (в соответствии с 8 квалитетом). = 16 мкм.

В тетради записываем:

Основное отклонение М – верхнее ES = -11+ = -11+16=5 мкм= 0,005 мм.

Вычисляем нижнее отклонение отверстия (по формуле 4)

EI =ES – TD = 0,005 – 0,045 = - 0,040 мм

2.Определяем предельные отклонения вала Ø52js7.

В обозначении поля допуска отверстия задан квалитет 7. Находим значение допуска. В таблице1.1 на пересечении строки интервала размеров от 50 до 80 мм (левый столбец) и столбца (квалитета) №7 указано значение допуска 30 мкм.

Записываем:

Допуск вала Td = IT7 = 30 мкм =0,030 мм

В обозначении поля допуска указан ряд основных отклонений js. В таблице основных отклонений валов – табл.1.2 находим ряд, обозначенный js, и в клеточке над ним видим, что наименование основного отклонения не указано. В столбце js записано «основные отклонения ». Это значит, что основными являются оба предельных отклонения: верхнее равно половине допуска со знаком плюс, а нижнее равно половине допуска со знаком минус.

В тетради записываем.

Основное отклонение js:

верхнее отклонение es = +IT7/2 =+ 0,030/2=+0,015 мм и

нижнее отклонение ei = -IT7/2 = -0,030/2= -0,015 мм.

Обозначение посадки с найденными предельными отклонениями

3.Вычисляем предельные размеры вала (используем формулы 2 и 3)

dmax = d+ es = 52+ 0,015=52,015 мм,

dmin = d+ ei = 52+ (-0,015)=51,985 мм.

и отверстия

Dmax = D + ES = 52 + 0,005 = 52,005 мм,

Dmin = D + EI = 52 + (-0,040) = 51,960 мм.

4.Строим схему полей допусков (построение ведем в произвольно выбранном масштабе, откладывая значения предельных отклонений от нулевой линии в миллиметрах; ширина прямоугольников произвольная).

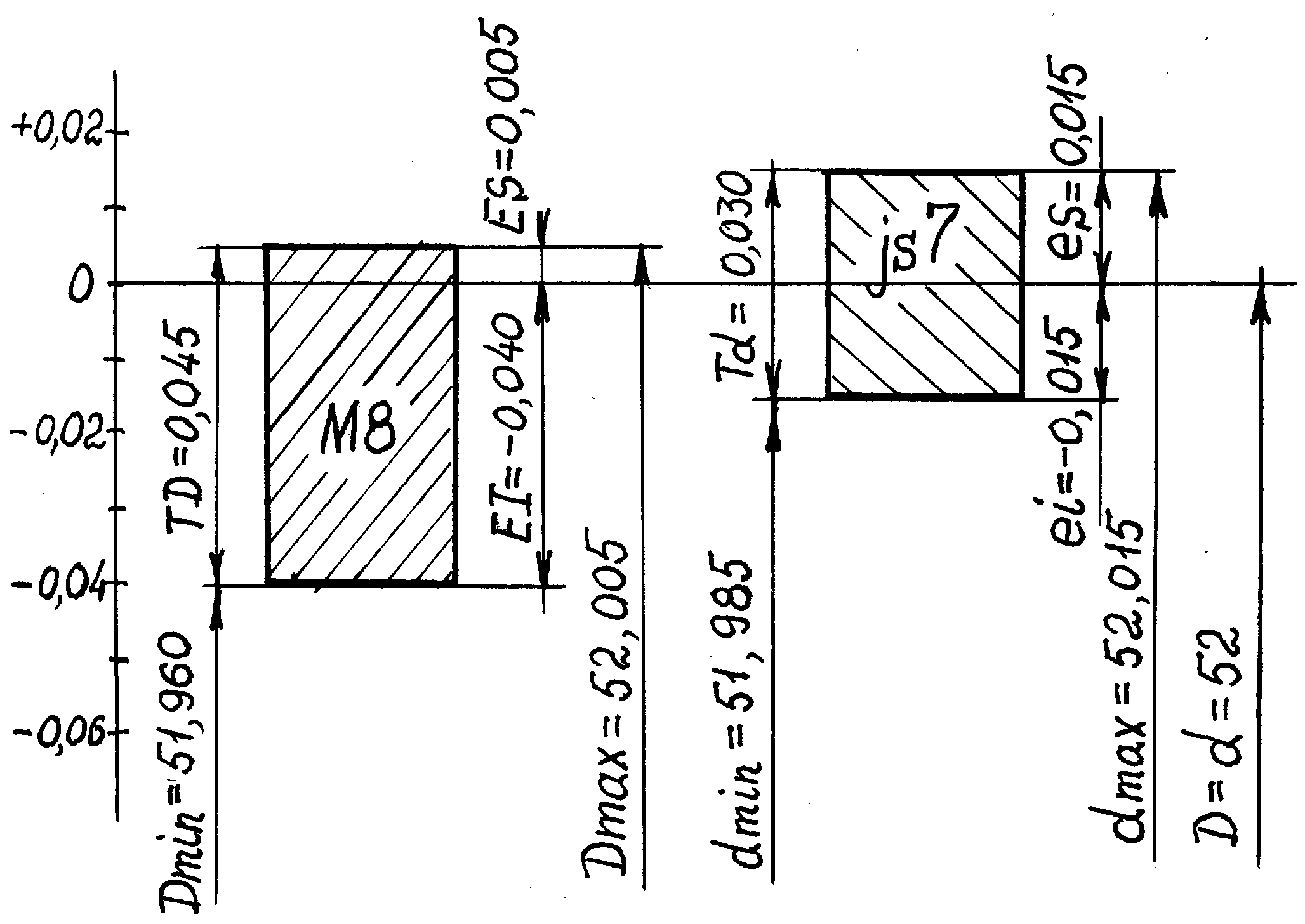
Анализируя рисунок (изображения полей допусков при перемещении вдоль линии номинального размера налагаются) или соотношение предельных размеров (не выполняется ни одно из условий dmin= 51,960 мм > Dmax =52,015 мм или Dmin =51,985 мм > dmax=52,005 мм, т.к. диапазоны предельных размеров/отклонений перекрываются), делаем вывод о виде посадки:

посадка переходная внесистемная (внесистемная, так как в заданном сопряжении не присутствуют ни основной вал, ни основное отверстие.)

Для переходной посадки определяем максимальный натяг и максимальный зазор по формулам (11), (12) и допуск посадки по формуле (13).

Максимальный натяг Nmax=es–EI =0,015 – (-0,040) =0,055 мм.

Максимальный зазор Smax =ES – ei=0,005 – (-0,015)=0,020 мм.