Определение универсальной газовой постоянной на установке фпт1-12 и ее компьютерном имитаторе

Методические указания к лабораторной работе

Цель работы – изучение газовых законов и экспери­мен­тальное определение универсальной газовой постоянной.

Приборы и принадлежности – установка ФПТ1-12, лабо­раторный термометр, IBM–совместимый персональный компьютер и пакет компьютерных программ, имитирующих работу лабораторной установки ФПТ1-12.

Теоретическое введение

Уравнение состояния идеального газа. В молекулярно-кине­тической теории идеальным называют теоретическую модель газа, удовлетворяющую следующим условиям:

• собственный объем молекул пренебрежимо мал по сравнению с объемом сосуда, в котором находится газ;

• потенциальная энергия взаимодействия молекул прене­бре­жимо мала по сравнению с кинетической энергией их хаотического движения;

• удары молекул газа о стенки сосуда являются абсолютно упругими.

Модель идеального газа была предложена Дж.Герапатом в 1847 г.

Состояние газа определяется рядом параметров, важнейшими из которых являются температура и давление. В термодинамике температура – это величина, характеризующая состояние термо­динамического равновесия макроскопической системы, а давление – сила, действующая на единицу площади поверхности в направлении нормали к ней. Молекулярно-кинетическая теория, опираясь на модель идеального газа, связывает температуру и давление с усред­ненными характеристиками движения молекул газа. В результате температура определяется как физическая величина, являющаяся мерой средней кинетической энергии поступательного движения молекул газа. Давление определяется суммарным импульсом, передаваемым молекулами в единицу времени единице площади поверхности сосуда, в котором находится газ.

Параметры состояния идеального газа связаны уравнением

, (1)

где , и –	соответственно давление, объем и масса газа;
 –	молярная масса, т. е. масса одного моля газа;
–	термодинамическая температура, измеряемая в кель­винах;
–	универсальная газовая постоянная.

Отношение определяет количество вещества или число молей идеального газа. Эту же величину можно получить, разделив число молекул в данной массе газа на постоянную Авогадро , определяющую число молекул в одном моле, т.е.

. (2)

После подстановки второго из выражений (2) в соотношение (1) уравнение состояния идеального газа принимает вид

, (3)

где – постоянная Больцмана.

Значения трех часто используемых в молекулярной физике постоянных приведены в табл.1.

Таблица 1

Наименование физической постоянной	Обозна-чение	Приближенное значение	Наиболее точно измеренное (табличное) значение
Постоянная Больцмана		1,3810-23 ДжК	1,380662(44)10-23 ДжК
Постоянная Авогадро		6,021023 моль-1	6,022045(31)1023 моль-1
Универсальная газовая постоянная		8,31 Дж(мольК)	8,31441 Дж(мольК)

Из уравнения (1) легко выводятся три опытных газовых закона:

• закон Бойля (1662 г.)  Мариотта (1676 г):

const при и ; (4)

• закон Шарля (1787 г.):

const при и ; (5)

• закон Гей-Люссака (1802 г.):

const при и const. (6)

Из уравнения (3) непосредственно следует закон Авогадро (1811 г.): в равных объемах газов при одинаковых давлении и температуре содержится одинаковое число молекул. Из этого уравнения также можно вывести закон Дальтона (1801 г.). Действительно, в случае смеси химически невзаимодействующих газов величина , входящая в уравнение (3), определяет полное число молекул, т.е. сумму чисел молекул разных сортов:

, (7)

где –	число молекул -го сорта;
–	число компонент смеси.

Подставив выражение (7) в уравнение (3), получим:

. (8)

С другой стороны, если бы весь объем занимали только молекулы -го сорта, то давление (парциальное давление) удовлетворяло бы соотношению

. (9)

Подставляя левую часть выражения (9) в правую часть уравнения (8), получим после сокращения на :

, (10)

что и является законом Дальтона: давление смеси химически невзаимодействующих идеальных газов равно сумме парциальных давлений.

Уравнение (1) часто называют уравнением Клапейрона–Менде­леева. Обоснованием этому послужили следующие обстоятельства. Сначала Б.П.Э.Клапейрон (1834 г.) объединил законы (4)-(6) и записал уравнение состояния идеального газа в виде

, (11)

где коэффициент пропорциональности зависит от массы газа и его молярной массы. Затем Д.И.Менделеев (1874 г.) объединил за­кон Авогадро с уравнением Клапейрона, ввел в него универ­сальную газовую постоянную и записал уравнение состояния в виде соотношения (1).

Ф

изический смысл постоянной . Для того чтобы выяснить физический смысл универсальной газовой постоянной, получим формулу для работы, которую совершает газ при расширении. Пусть газ заключен в цилин­д­ри­чес­кий сосуд с поршнем, при дви­же­нии которого из­меняется объем газа (рис. 1). Сила воздействия газа на поршень площадью равна , и, следовательно, фор­мулу для работы, совершаемой при бесконеч­но малом пере­мещении поршня , можно записать в виде

, (12)

где – изменение объема газа.

Из уравнения (12) следует, что при расширении газа от объема до объема он совершает работу

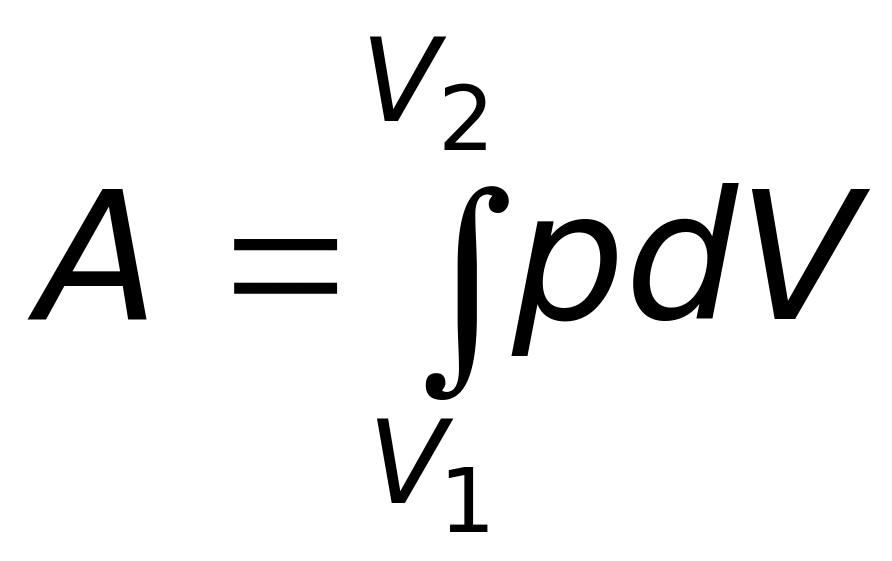. (13)

Применим формулу (13) к изобарному ( ) расширению газа и воспользуемся соотношениями (1) и (2). В результате получим:

, (14)

откуда

. (15)

Формула (15) и раскрывает физический смысл постоянной : универсальная газовая постоянная – это величина, численно равная работе, которую совершает один моль идеального газа при его изобарном расширении в результате нагревания на 1 К.