Рекомендации к выполнению и оформлению домашнего задания.

Работа оформляется на бумаге стандартного образца с обязательной нумерацией страниц и наличием на них стандартного поля. Она должна содержать задание, таблицу исходных данных, основные формулы, по которым выполнялись расчеты, таблицы 2, 7-15, рисунки 6, 7, 9, 14, 17, 19 и 20, приведенные в Приложении 1 к Методическим указаниям, выводы по каждому разделу и по работе в целом. Примеры формулировки выводов приведены в первом и во втором разделах указанного приложения.

Готовую работу необходимо сброшюровать, оформить титульный лист и содержание, указать список использованной литературы.

В течение времени, предусмотренного для выполнения домашнего задания, в соответствии с графиком самостоятельной учебной работы, студент может консультироваться с преподавателем.

Целью расчетов в домашнем задании являются не числа, а понимание исследуемого процесса. Вместе с тем, из ошибочных результатов вытекают и соответствующие им выводы. Поэтому при защите домашнего задания студент должен показать знания и навыки выявления закономерностей в случайных явлениях и процессах, способность делать правильные выводы, обоснованные достаточно точными расчетами.

Приложение 1

к Методическим указаниям

к выполнению домашнего задания по дисциплине «Статистика».

Раздел «Общая теория статистики»

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Государственный университет управления

Институт финансового менеджмента

Кафедра статистики

Домашнее задание по дисциплине «Статистика»

Раздел «Общая теория статистики»

Вариант № __

Выполнил: студент __ курса __ группы Сроки сдачи:

Иванов В.В. плановый: ________

фактический: _________

Проверил: Петров П.П.

Москва – 2006

Исходные данные приведены в табл. 1

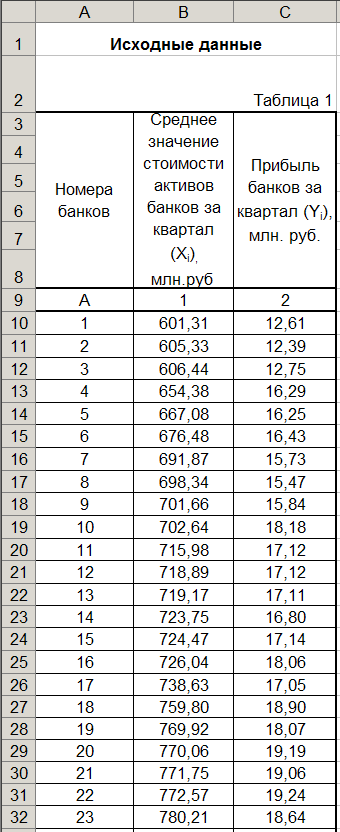
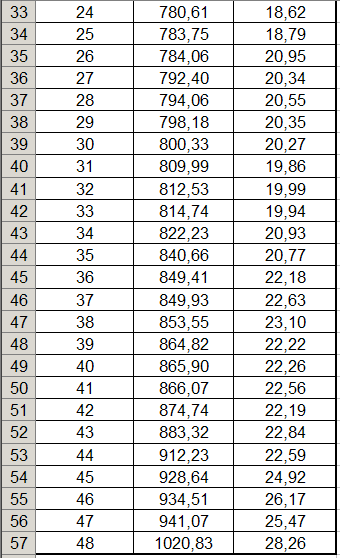
1.ПРОВЕРКА ПЕРВИЧНОЙ ИНФОРМАЦИИ НА ОДНОРОДНОСТЬ, НАЛИЧИЕ АНОМАЛЬНЫХ НАБЛЮДЕНИЙ И НОРМАЛЬНОСТЬ РАСПРЕДЕЛЕНИЯ

Совокупность считается однородной, если коэффициент ее вариации меньше 33%.

, (1)

где - среднее значение; (2)

- среднее квадратическое отклонение; (3)

n – объем совокупности.

Среднее значение вычисляется с помощью функции СРЗНАЧ. Ячейка В60 табл. 2 содержит формулу = СРЗНАЧ (В10:В57), по которой рассчитывается среднее значение активов банков ( )

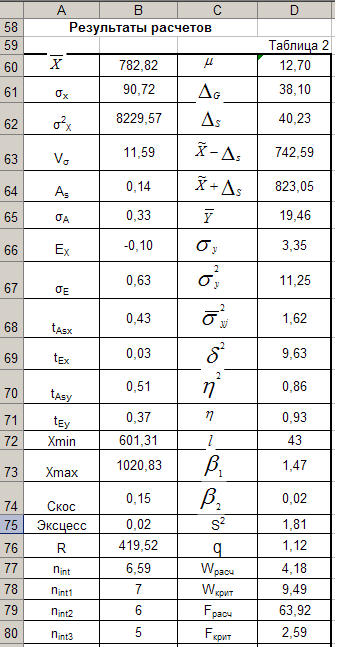
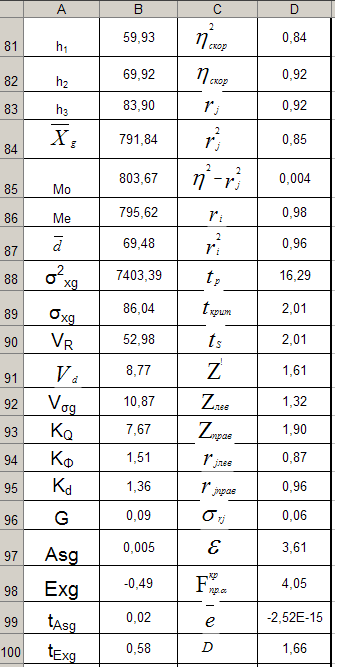
Среднее квадратическое отклонение рассчитывается в предположении, что данные представляют всю генеральную совокупность. В ячейку В61 записана формула СТАНДОТКЛОНП (В10:В57), .

В ячейку В63 записана формула (1), т.е. = В61/В60*100. Коэффициент вариации равен 11,59%.

Если исходные данные являются эмпирическими, то их необходимо проверить на наличие аномальных наблюдений (резко выделяющихся единиц совокупности):

(4)

или , (5)

.

Если условия (4) или (5) не выполняются, то соответствующие единицы совокупности исключаются из дальнейшего рассмотрения, а значения пересчитываются.

Минимальное и максимальное значения совокупности находятся в ячейках В72 и В73.

Из приведенных данных следует, что условие (4) выполняется.

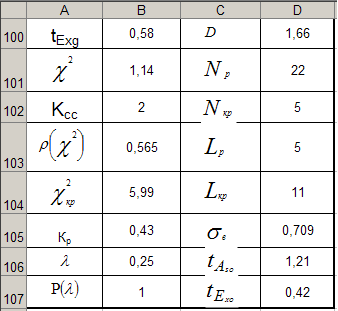
Гипотеза о нормальном распределении активов банков принимается, если выполняются оба соотношения:

, (6)

где - относительный показатель ассиметрии; (7)

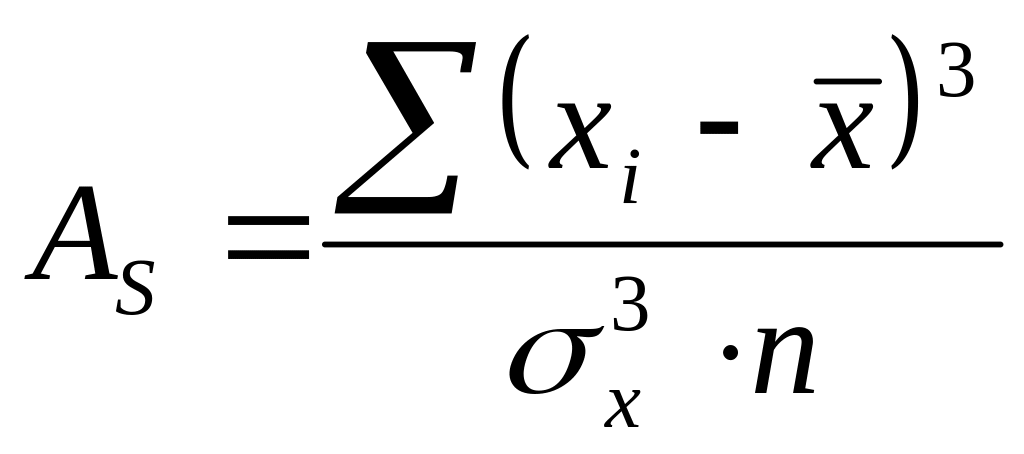- показатель ассиметрии; (8)

- средняя квадратическая ошибка асимметрии; (9)

- относительный показатель эксцесса; (10)

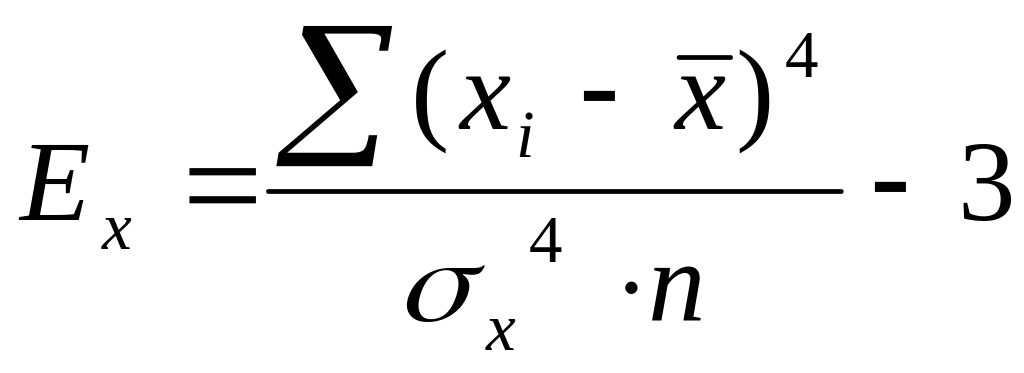- показатель эксцесса; (11)

- средняя квадратическая ошибка эксцесса. (12)

Для вычисления показателя асимметрии в ячейку В64 записана формула (8) = СУММПРОИЗВ((В10:В57-$В$60)^3) /($В$61^3*$A$57). Формула для вычисления эксцесса аналогична предыдущей и отличается показателем степени и наличием вычитаемого числа равного 3. Она реализована в ячейке В66=СУММПРОИЗВ((В10:В57-$В$60)^4)/($В$61^4*$A$57)-3. Учитывая, что оба относительных показателя ( и ) меньше 1,5, гипотезу о нормальном распределении активов банков следует принять.

В EXCEL для вычисления показателей асимметрии и эксцесса существуют функции СКОС и ЭКСЦЕСС. В них реализованы приближенные формулы для вычисления перечисленных показателей выборочных совокупностей. Использовать их нецелесообразно в связи с тем, что ранее было принято допущение, что исходная совокупность является генеральной.

Анализ результатов расчета позволяет сделать следующие выводы:

1. Совокупность активов банков однородна ( ), следовательно, средняя величина является обобщающей характеристикой активов банков и отражает типичный уровень в расчете на один банк в конкретных условиях места и времени.

2. Аномальные наблюдения отсутствуют.

3. Распределение активов банков плосковершинно и имеет правостороннюю асимметрию. Отклонения эмпирических частот от теоретических носят случайный характер, следовательно эмпирическое распределение активов банков не противоречит нормальному.