6.5.Основи операторного методу.

Перетворення Лапласа та його основні властивості.

В основі операторного методу дослідження перехідних процесів лежить інтегральне перетворення Лапласа. Нехай функція дійсної змінної визначена при і задовольняє умовам:

1. На будь якому скінченому проміжку функція неперервна, за виключенням, можливо, декількох точок розриву першого типу.

2. при .

3. Існують такі постійні та , що для усіх виконується нерівність

.

Перетворенням Лапласа функції називається функція комплексної змінної

. (7.21)

Функцію , що задовольняє умовам 1- 3 називають оригіналом, а її перетворення Лапласа , тобто - зображенням функції . Зв’язок між оригіналом та його зображенням умовно позначатимемо так:

.

До речі, як правило, математичні моделі реальних сигналів задовольнять умовам 1- 3 .

Зупинимося лише на тих властивостях інтегрального перетворення Лапласа, які будуть використовуватися при розрахунку перехідних процесів.

Лінійність. Формула (7.21) лінійна відносно підінтегрального множника , отже перетворення Лапласа лінійне, тобто якщо , то - зображення лінійної комбінації оригіналів є лінійною комбінацією зображень.

З

Рис.7. 8

ображення найпростіших функцій. Оскільки перетворення Лапласа є одностороннім, то усі наступні функції, що заслуговують нашої уваги визначені лише при . При - . Знайдемо зображення функції . Графік цієї функції показаний на рис.7.8 Застосуємо інтегральне перетворення Лапласа:

.

Отже

Рис.7. 9

. (7.22)

Це єдина із багатьох формул перетворення Лапласа яку доцільно запам’ятати.

Отриманий результат дає можливість знайти зображення функції включення (функції Хевісайда) показаної на рис.7.9. Оскільки , то

.

Очевидно, що

1. .

2. .

3. .

4. .

5. .

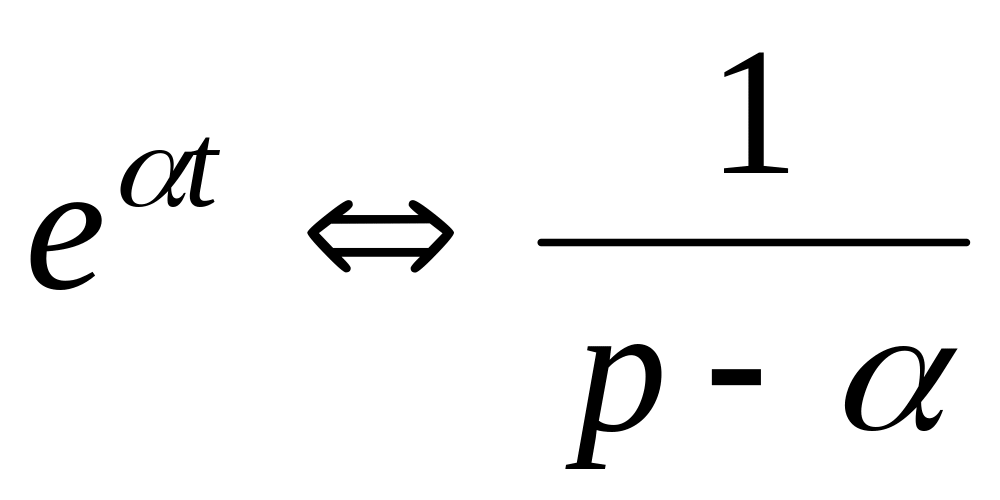Значну кількість зображень різноманітних функцій можна знайти у спеціальній літературі []. Розширити їх число можна з допомогою теореми про зміщення та теореми про запізнення.

Теорема про зміщення стверджує, що якщо то . Насправді

. Теорема доведена.

Теорема про запізнення установлює зв’язок між зображеннями двох функцій (сигналів) зсунутих у часі : якщо то . Доведення теж елементарне.

Зображення похідної від функції.. Нехай . Знайдемо зображення від :

. Застосовуючи інтегрування по частинам, отримаємо:

. (7.23)

Зображення від другої похідної:

.

При нульових початкових умовах:

;

;

.

Зображення інтегралу від функції.. Нехай . Знайдемо зображення від . Позначимо . Очевидно, що , а . Якщо то скориставшись формулою (7.23) отримаємо: . Звідки

. (7.24)

Приклад 2. Знайти зображення функції .

Рішення . Оскільки , то використовуючи властивість лінійності перетворення Лапласа і той факт , що , отримаємо

.

Отже .