Приложение б Решение систем линейных алгебраических уравнений методом Гаусса, методом Крамера в среде Mathcad

Векторные и матричные операторы и функции системы Mathcad позволяют решать широ­кий круг задач линейной алгебры. К примеру, если заданы матрица A и матрица-столбец (называемая в Mathcad вектором) В для системы линейных уравнений в матричной форме AX=B, то решение можно получить из очевидного выражения X=A^-1B. Кроме рассмотрен­ного матричного метода решения систем линейных алгебраических уравнений, существует еще ряд методов решения таких систем. Рассмотрим, каким образом реализуются в Mathcad методы Крамера и Гаусса.

Метод Крамера.

Задание 1. Решить систему линейных алгебраических уравнений методом Крамера . Решение задания на рисунке 12.

Возможности Mathcad позволяют использовать метод Крамера не только при на­хождении решения невырожденной системы, но и для нахождения общего решения сис­темы, имеющей бесконечно много решений. Для этого используется нахождение определителя как функции, зависящей от свободных переменных.

Задание 2. Решить систему методом Крамера. Решение задания на рисунке 13.

Метод Гаусса в системе Mathcad можно осуществить с помощью функции rref.

Задание 3. Найдите решение системы линейных уравнений

с помощью функции rref. Решение задания на рисунке 14.

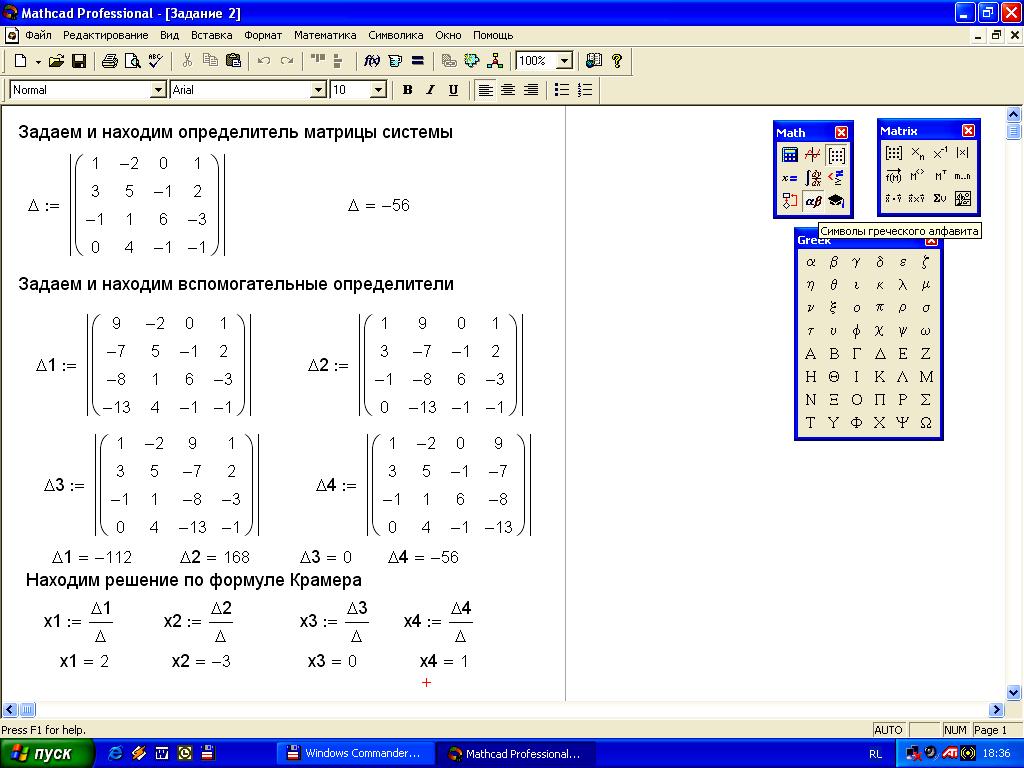
Рисунок 12

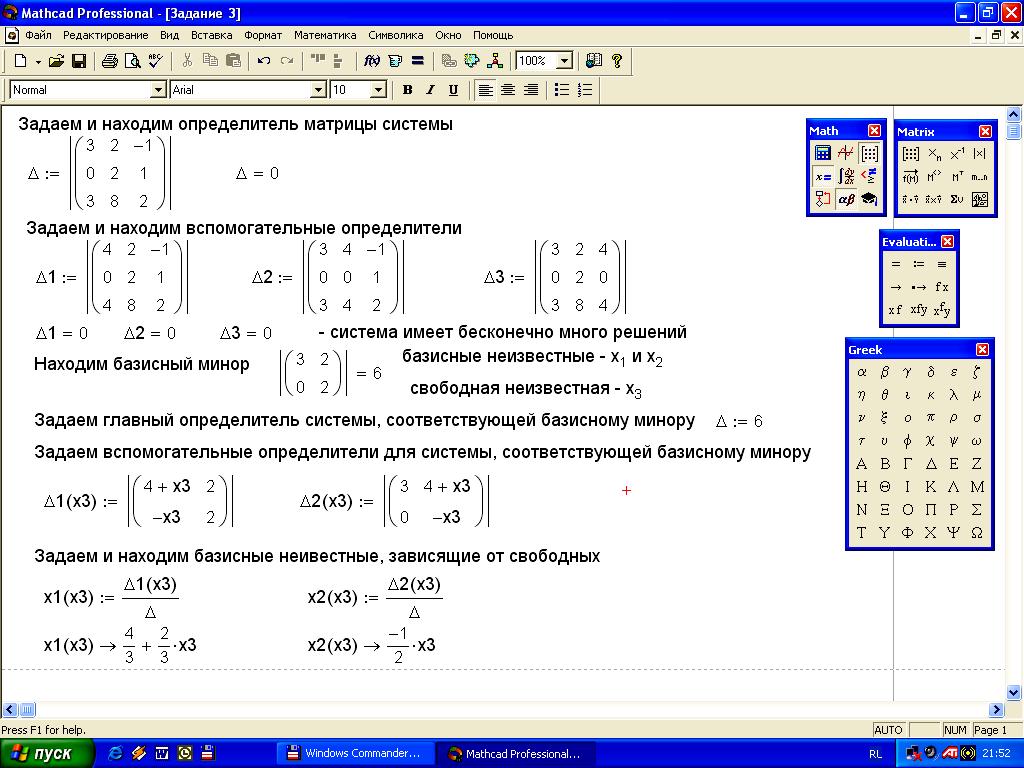
Рисунок 13

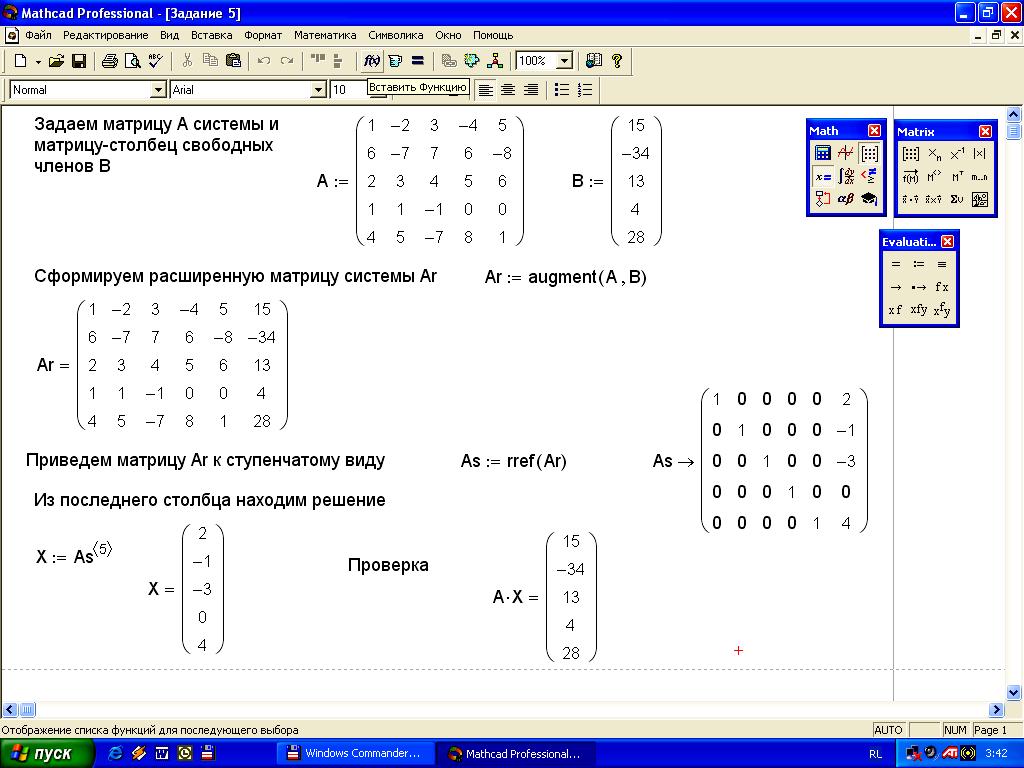
Рисунок 14

Задание 4. Исследовать систему на совместность. Если система совместна, то найти ее общее решение. Решение задания на рисунке 15.

Возможен еще один способ решения системы линейных уравнений в Mathcad с помощью функции lsolve.

Задание 5. Решить систему линейных уравнений

с применением функции lsolve. Решение задания на рисунке 16.

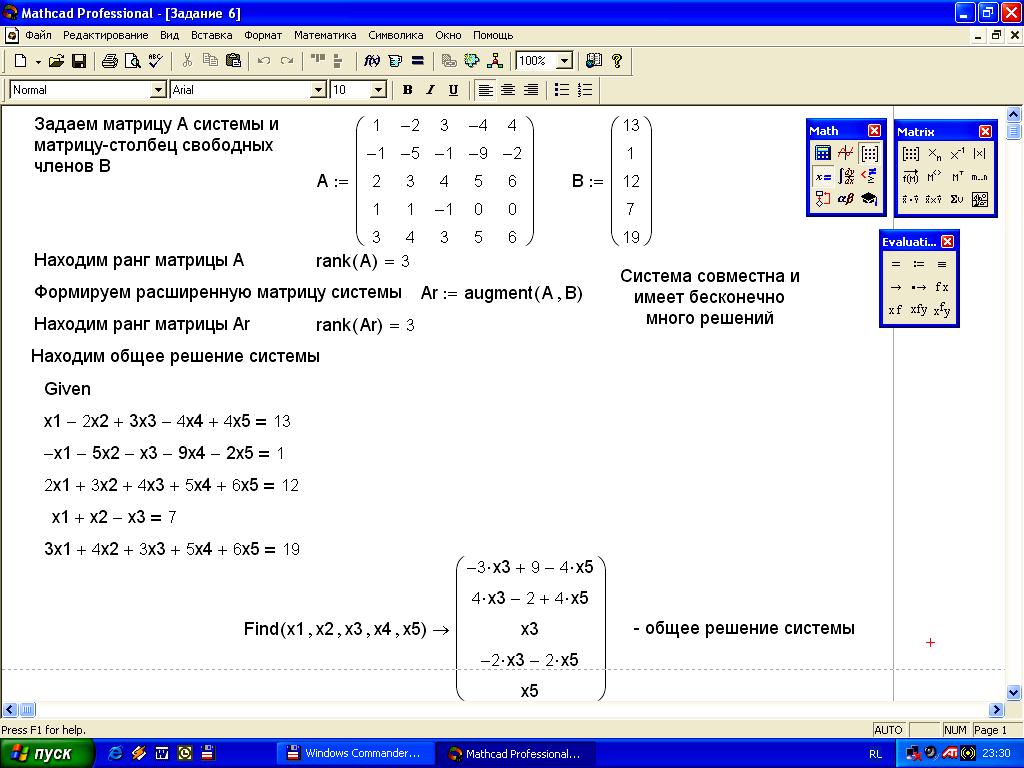
Рисунок 15

Рисунок 16

Приложение в Построение кривых второго порядка в среде Mathcad

Построение кривых на плоскости, заданных в декартовых координатах в системе Mathcad.

Для построения графиков используются шаблоны. Их можно выбирать двумя способами.

1. Выбор шаблона с помощью подменю График в меню Вставка (рисунок 17)

2. Выбор шаблона с помощью панелей инструментов. Для этого в панели Math необходимо щелкнуть по кнопке Graph (инструменты графиков) (рисунок 18). Затем щелчком по кнопке панели Graph вставить поле графика соответствующего типа (рисунок 19).

Незаполненный шаблон графика представляет собой большой пустой прямоугольник с шаблонами-местами ввода данных в виде темных маленьких прямоугольников, располо­женных около осей абсцисс и ординат будущего графика. В них необходимо ввести выра­жения, задающие координаты точек графика по осям абсцисс и ординат. В общем случае это могут быть функции некоторой переменной x.

Рисунок 17

Рисунок 18 Рисунок 19

Если график уже построен, то при его выделении появляются крайние места ввода с авто­матически введенными числами, которые служат для указания предельных значений абс­цисс и ординат, то есть задают масштаб графика. Сначала рекомендуется использовать ав­томатическое масштабирование, а лишь затем выбирать более походящий масштаб.

Особое внимание при построении графика следует уделить заданию пределов изменения переменной x. Различают упрощенный способ без задания ранжированной переменной, при котором пределы изменения задаются автоматически, и обычный способ с заданием ранжированной переменной. Упрощенный способ был рассмотрен ранее. При обычном способе необходимо ввести саму функцию и интервал её изменения, а лишь затем выби­рать шаблон.

Форматирование двухмерных графиков.

Вид графика можно изменять при помощи команд форматирования графиков. Для измене­ния формата уже построенного графика необходимо его выделить, щелкнув по нему. Вы­деленный график обводится сплошной линией с маркерами изменения размера.

Затем к выделенному графику можно применить команду Формат из главного меню и выбрать и выбрать в ней подменю график (рисунок 20). При этом появляется диалоговое окно форматирования (рисунок 21).

Это же диалоговое окно появится, если щелкнуть по выделенному графику правой копкой мыши и выбрать в появившемся меню подменю Формат или дважды щелкнуть левой кнопкой мыши по графику.

Рисунок 20

Диалоговое окно форматирования имеет четыре вкладки:

Оси X-Y – задание параметров отображения осей;

Трассировки (Линии) – задание параметров отображения линий графика;

Метки – задание параметров отображения меток (надписей) у осей;

Умолчание – задание параметров по умолчанию.

Все параметры форматирования относятся к выделенному графику и могут при необходи­мости меняться.

Рисунок 21

Задание1. Построить график функции , выбрав шаблон любым из описанных способов. Задайте более подходящий масштаб. Измените стиль осей графика. Измените цвет линий графика. Задайте надписи у осей. Решение задания на рисунке 23.

Задание 2. Построить в одной системе координат графики трех функций. Решение задания на рисунке 24.

Задание 3. Построить кривую . Определить тип кривой. Решение задания на рисунке 25.

Задание 4. Построить кривые и , найти их точки пересечения. Решение задания на рисунках 26 и 27.

В пакете Mathcad также возможно построение кривых, заданных в полярных координатах и в параметрической форме. Примеры таких построений приведены на рисунках 28 и 29.

Рисунок 23

Рисунок 24

Рисунок 25

Рисунок 26

Рисунок 27

Рисунок 28

Рисунок 29