2. Найти точки пересечения кривых второго порядка

1) , . 2) .

3) 4)

5) . 6) .

7) . 8) .

9) . 10) .

11) . 12) .

13) . 14) .

15) . 16) .

3 Определить вид кривой, заданной уравнением , построив её

а) ,

б)

в)

г)

д)

е)

ж)

Лабораторная работа № 4

Тема: Построение поверхностей второго порядка.

Цель: Рассмотреть возможности построения поверхностей второго порядка в системе Mathcad

Порядок выполнения работы:

1) Повторить некоторые теоретические сведения, известные из курса аналитической геометрии, необходимые для выполнения работы.

2) Рассмотреть примеры построения поверхностей второго порядка в Mathcad в Приложении Г.

3) Выполнить задачи для самостоятельного решения по вариантам. Вариант соответствует порядковому номеру в журнале.

4) Написать отчет (в свободной форме).

Основные теоретические сведения, необходимые для выполнения лабораторной работы.

Общее уравнение поверхности второго порядка. относительно некоторой прямоугольной системы координат имеет вид:

(4.4)

где .

Существует 17 поверхностей второго порядка в пространстве, описываемых в таблице 2

Таблица 2.

№	Каноническое уравнение	Название	Вид
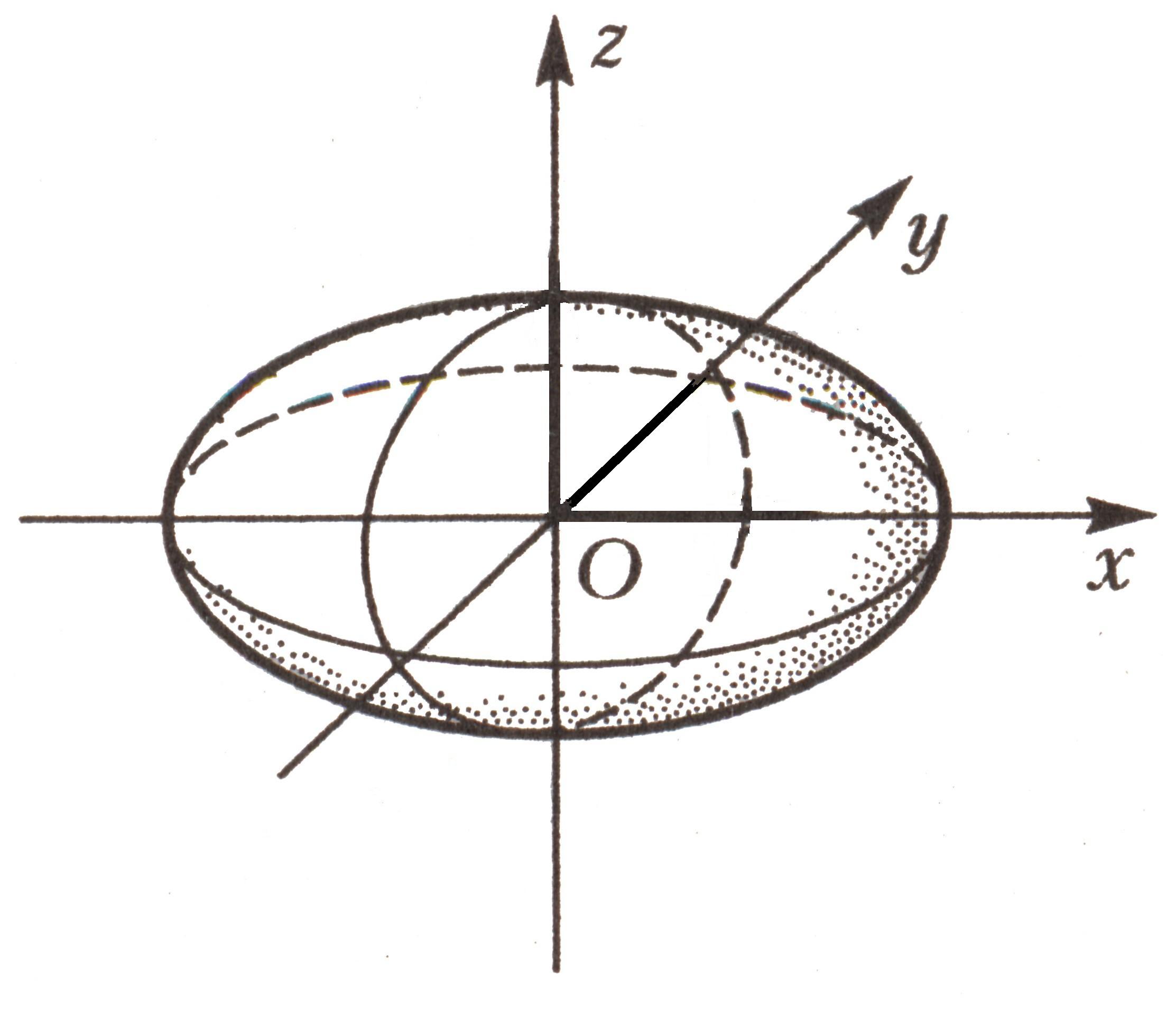
1		Эллипсоид
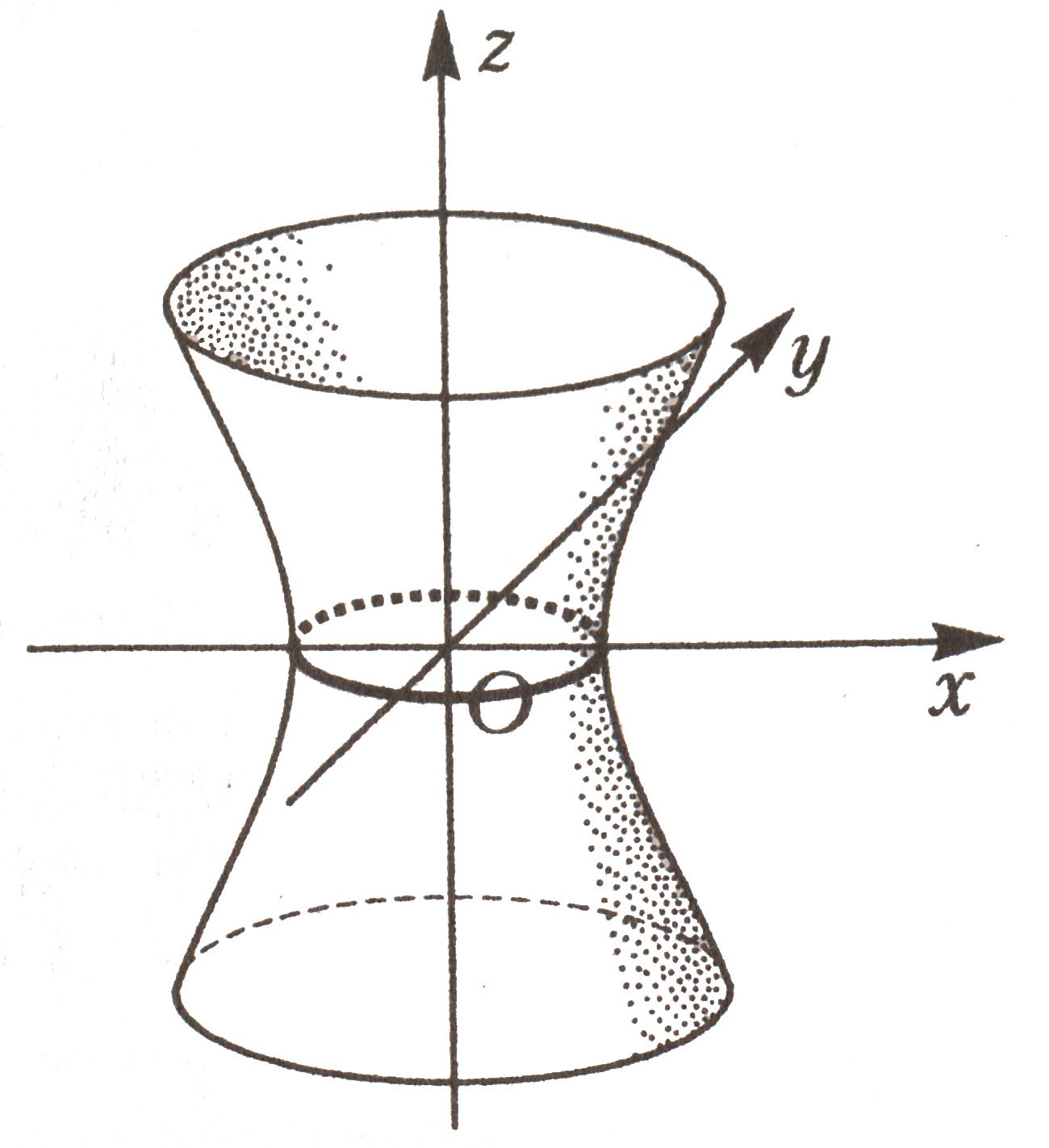
2		Однополостный гиперболоид
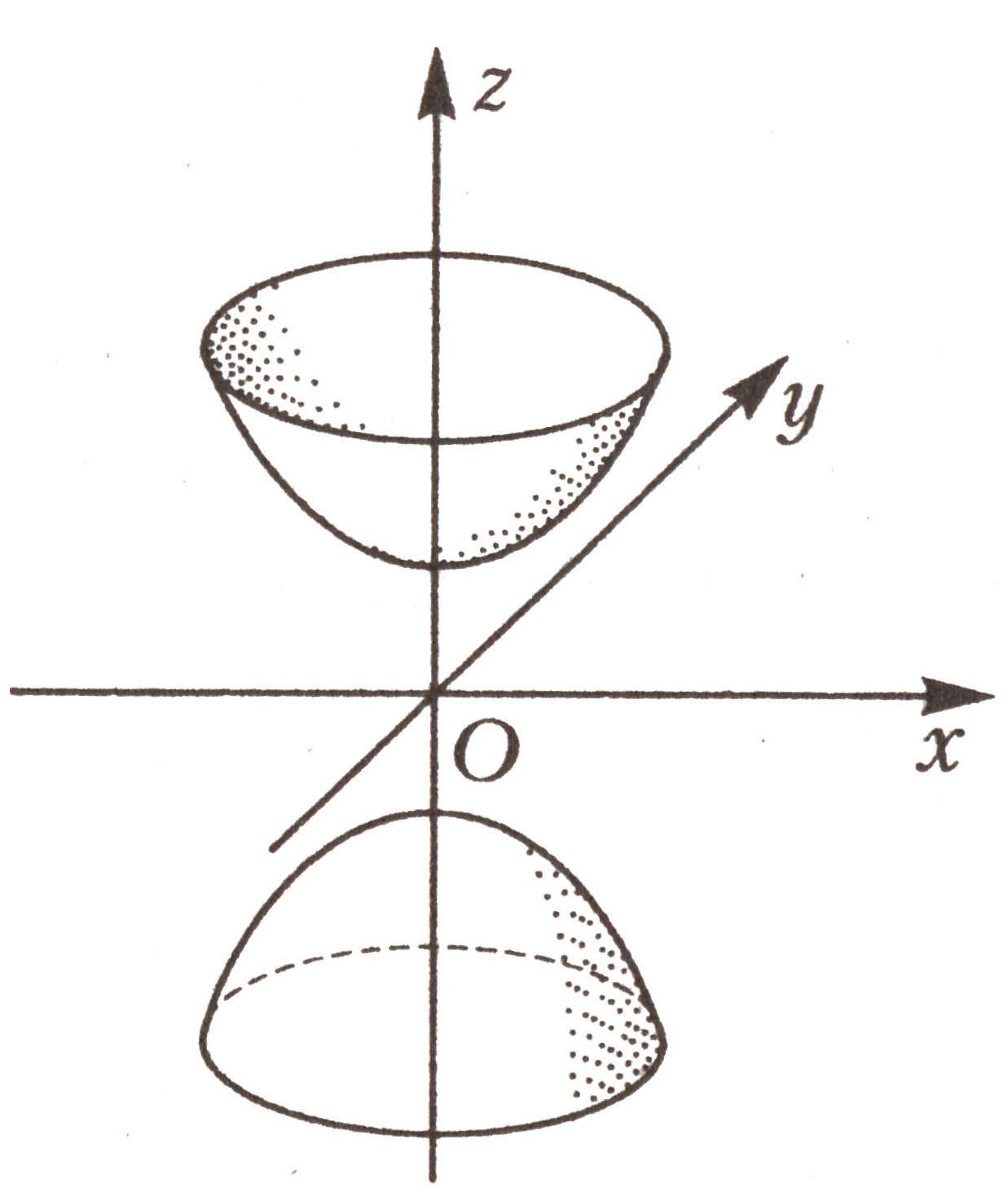
3		Двуполостный гиперболоид
4		Эллиптический параболоид
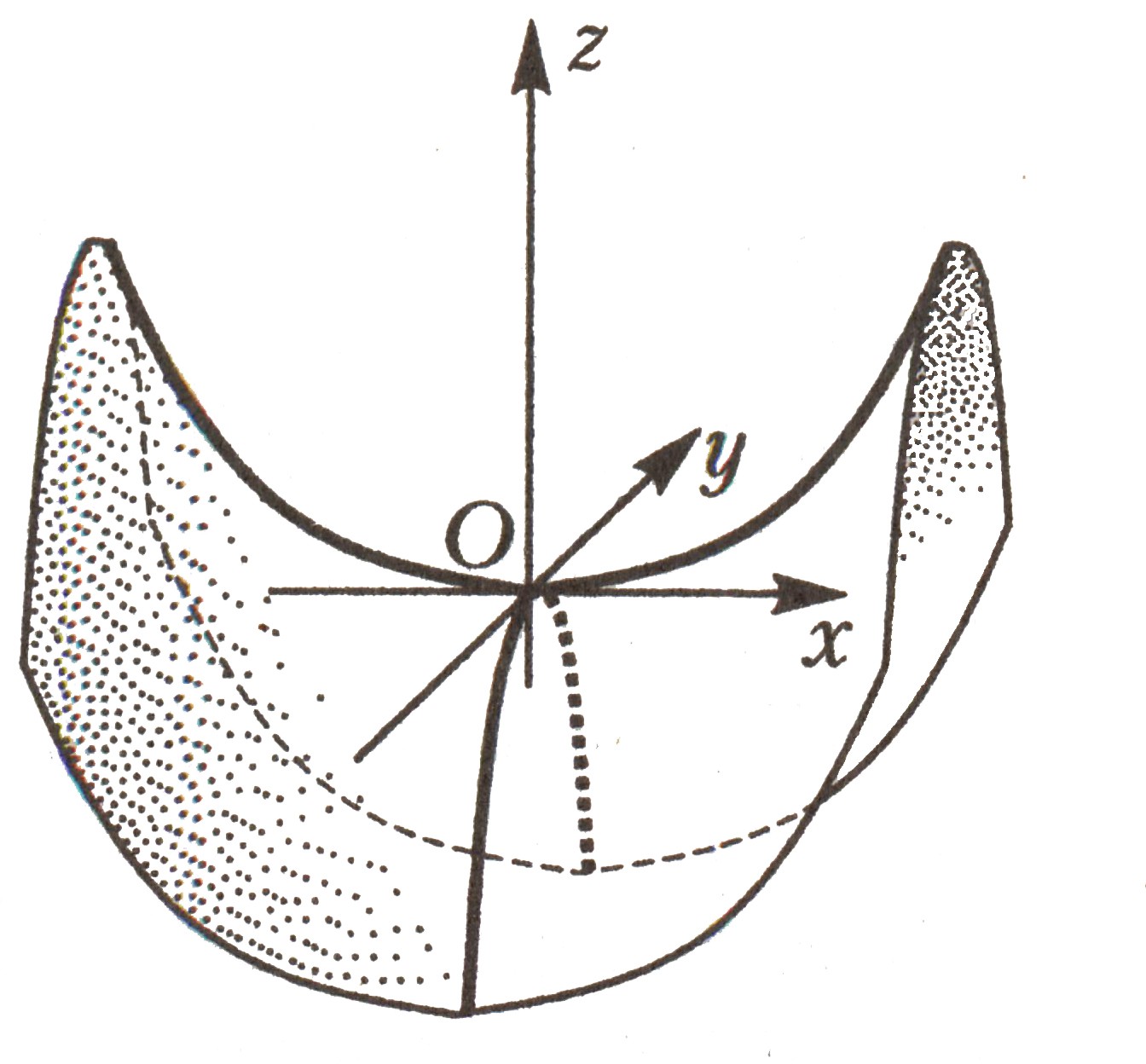
5		Гиперболический параболоид
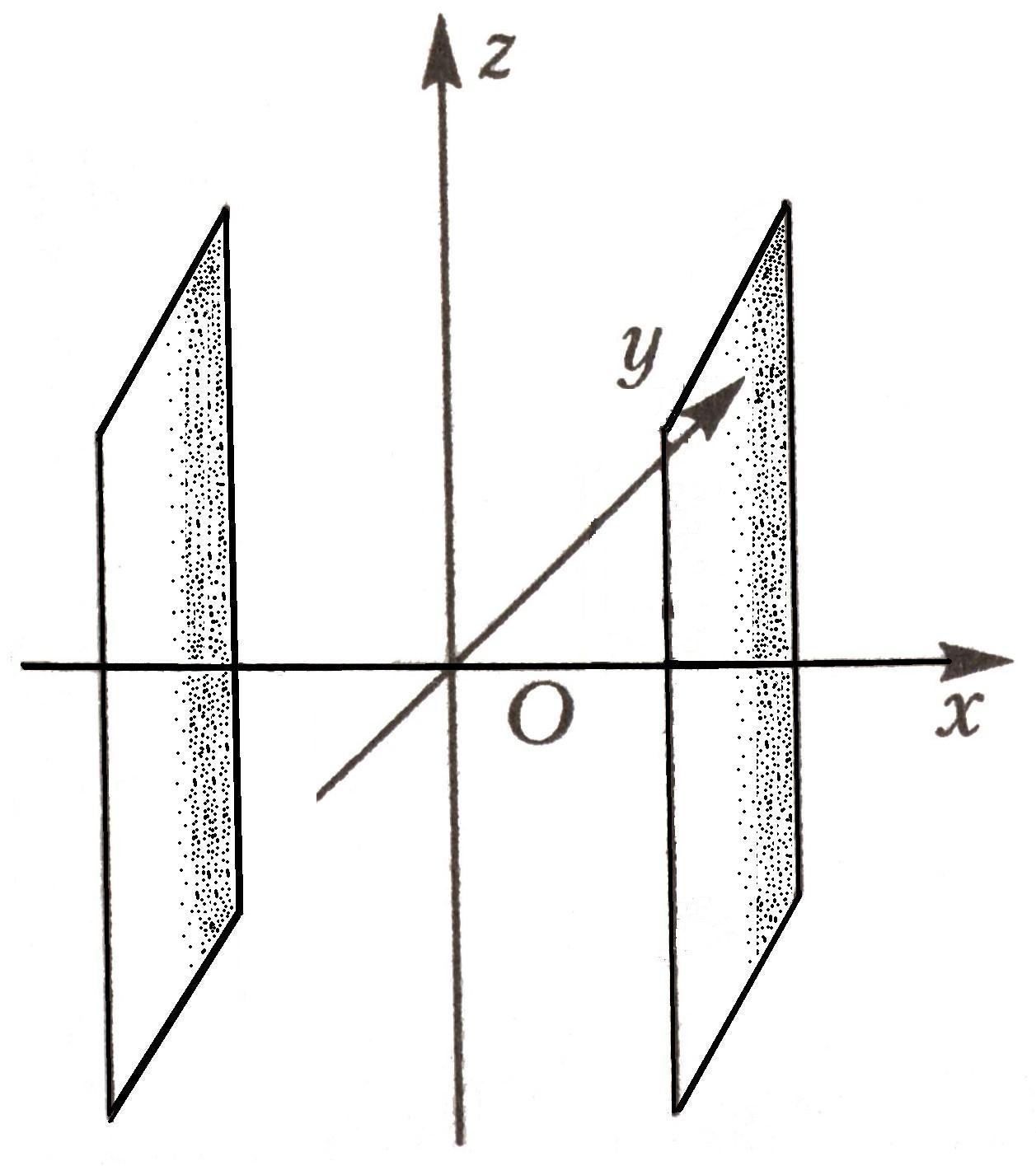
6		Эллиптический цилиндр
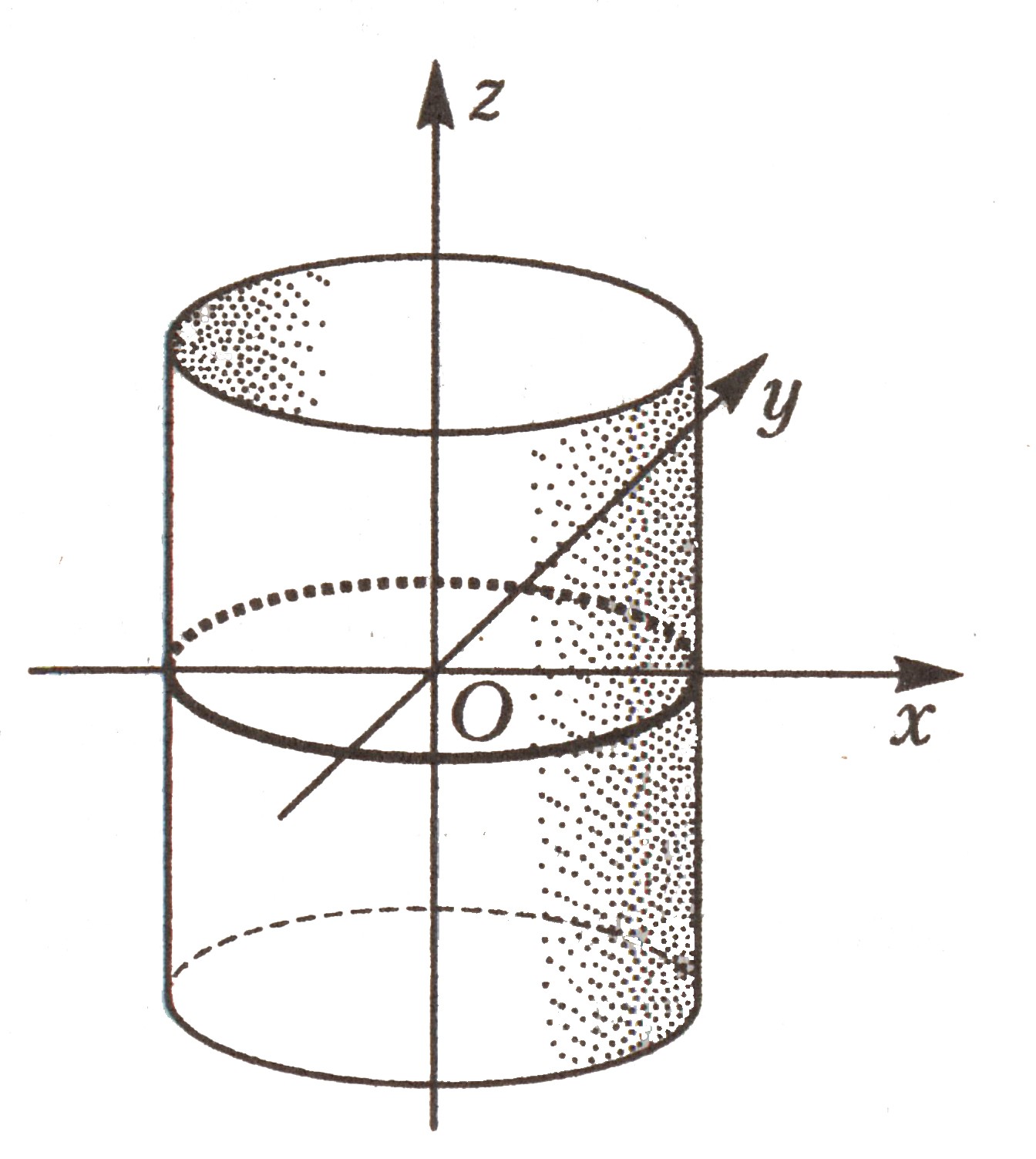
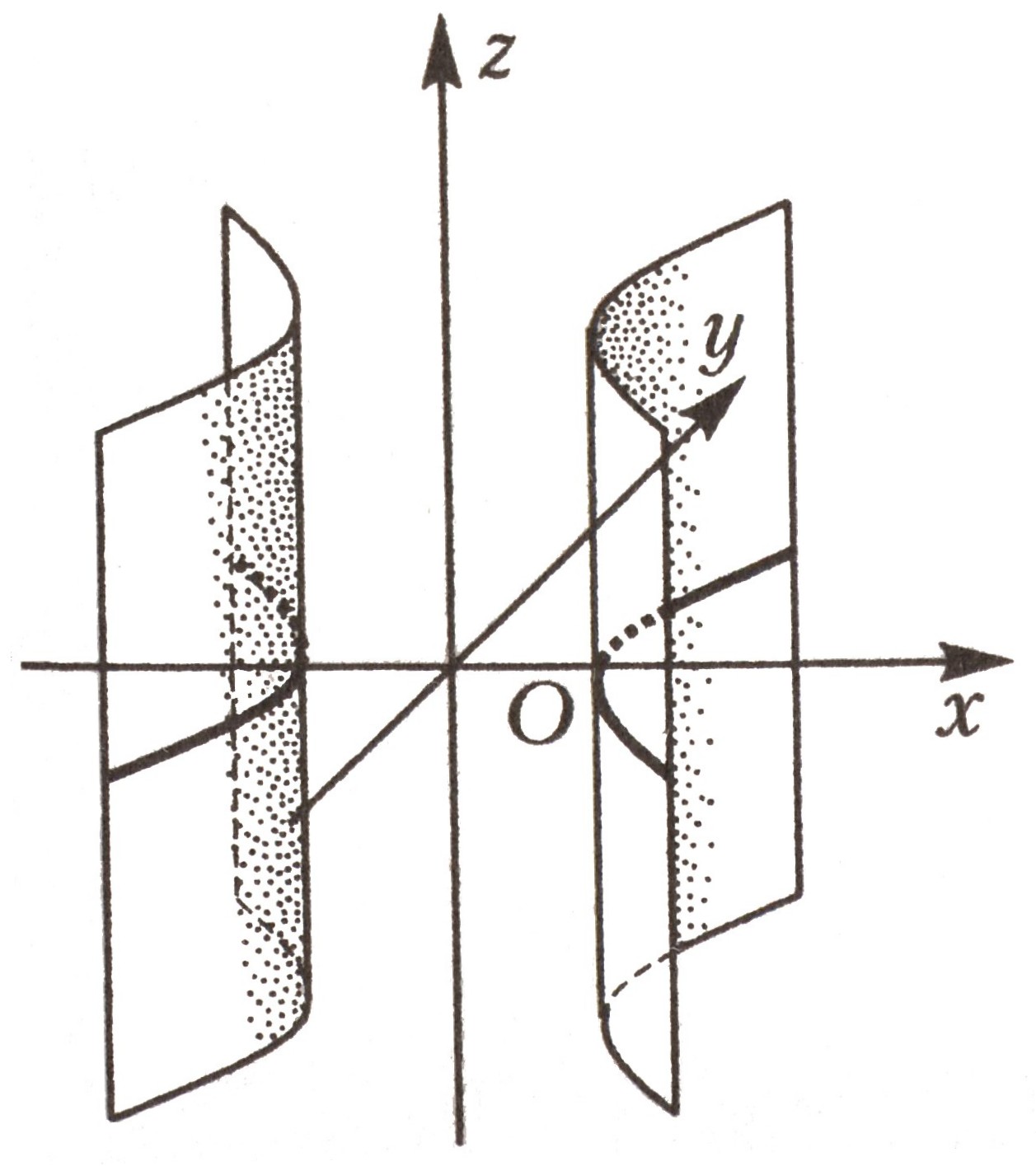
7		Гиперболический цилиндр
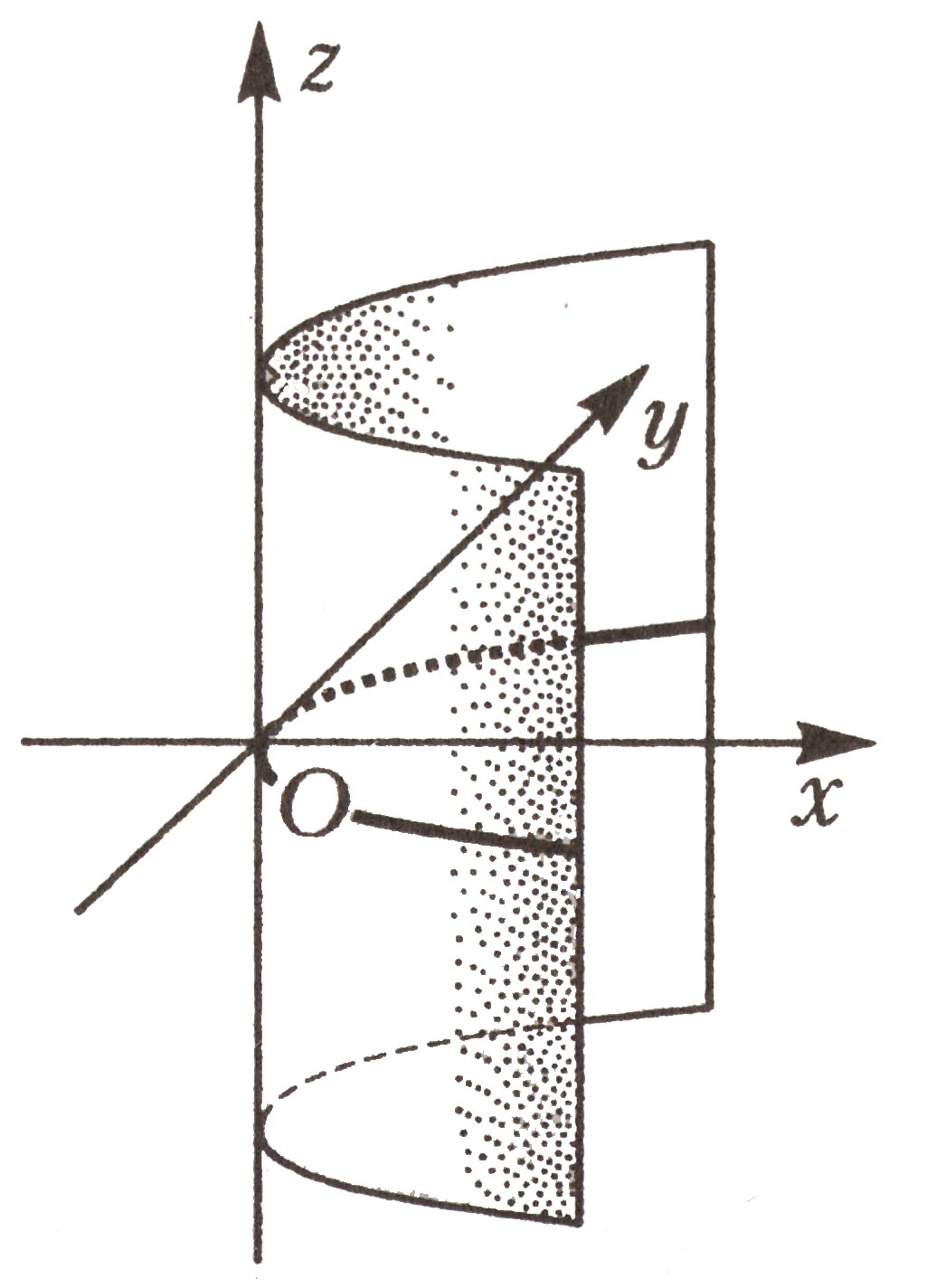
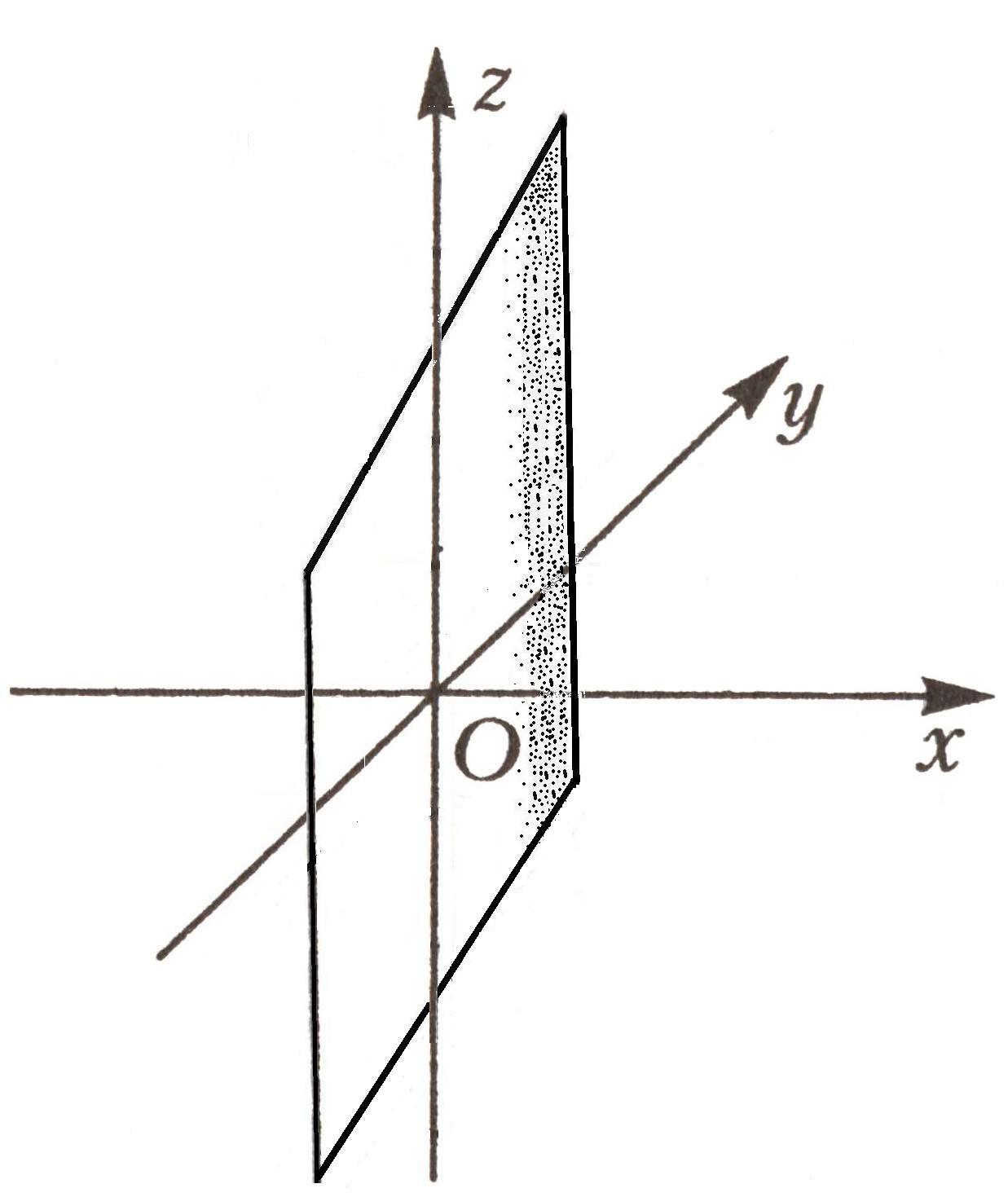
8		Параболический цилиндр
9		Мнимый эллиптический цилиндр
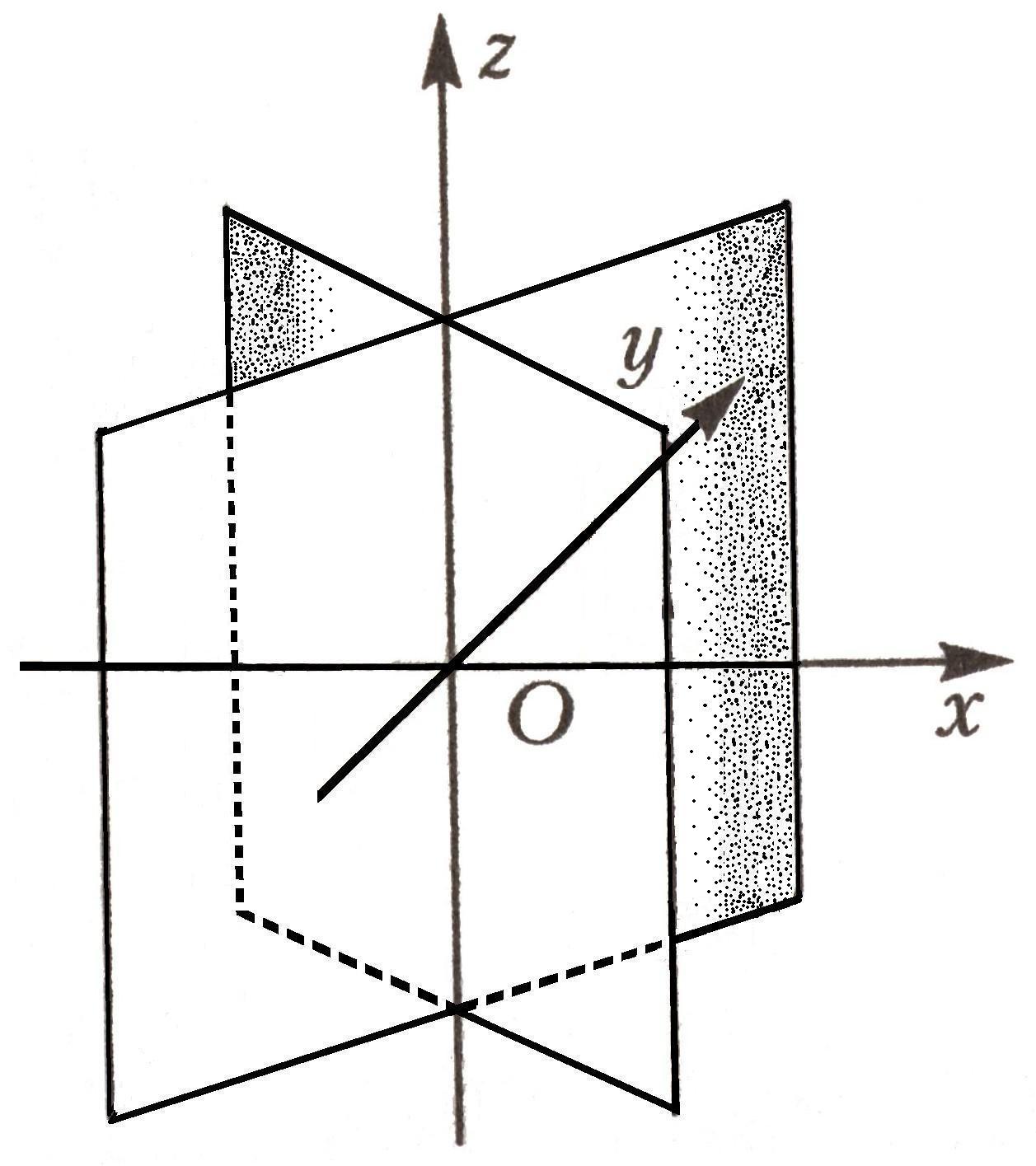
10		Пара действительных пересекающихся плоскостей
11		Пара действительных параллельных плоскостей
12		Пара мнимых параллельных плоскостей
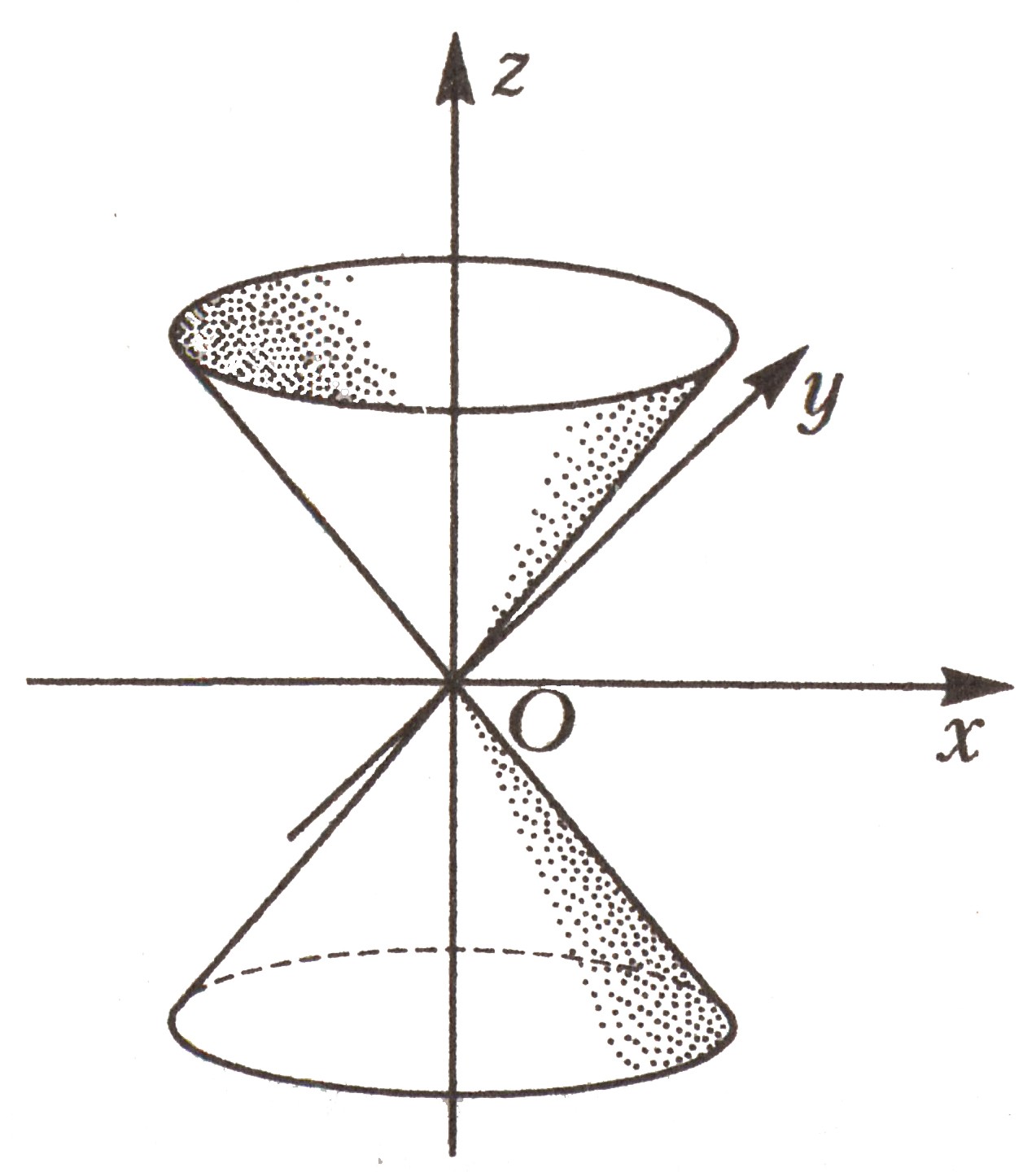
13		Конус II порядка
14		Пара мнимых пересекающихся плоскостей
15		Пара совпавших плоскостей
16		Мнимый конус
17		Мнимый эллипсоид

Задания для самостоятельного выполнения:

1 Построить следующие поверхности второго порядка

1) ; 2) ;

3) ; 4) ;

5) ; 6) ;

7) ; 8) ;

9) ; 10) ;

11) ; 12) ;

13) ; 14) ;

15) ; 16) .