- •Методические указания
- •Содержание
- •Введение
- •Лабораторная работа № 1
- •Основные теоретические сведения, необходимые для выполнения лабораторной работы.
- •1. Проверить выполнение свойств 1-8 для матриц а, в, с и чисел , :
- •Основные теоретические сведения, необходимые для выполнения лабораторной работы.
- •I Решение невырожденных систем
- •1 Метод Крамера
- •2 Метод Гаусса
- •3. Матричный метод
- •II Решение произвольных систем линейных уравнений
- •Рассмотрим матрицы
- •Доказать, что система имеет ненулевые решения. Найти несколько из них.
- •Основные теоретические сведения, необходимые для выполнения лабораторной работы.
- •Каноническое уравнение эллипса имеет вид
- •Гипербола
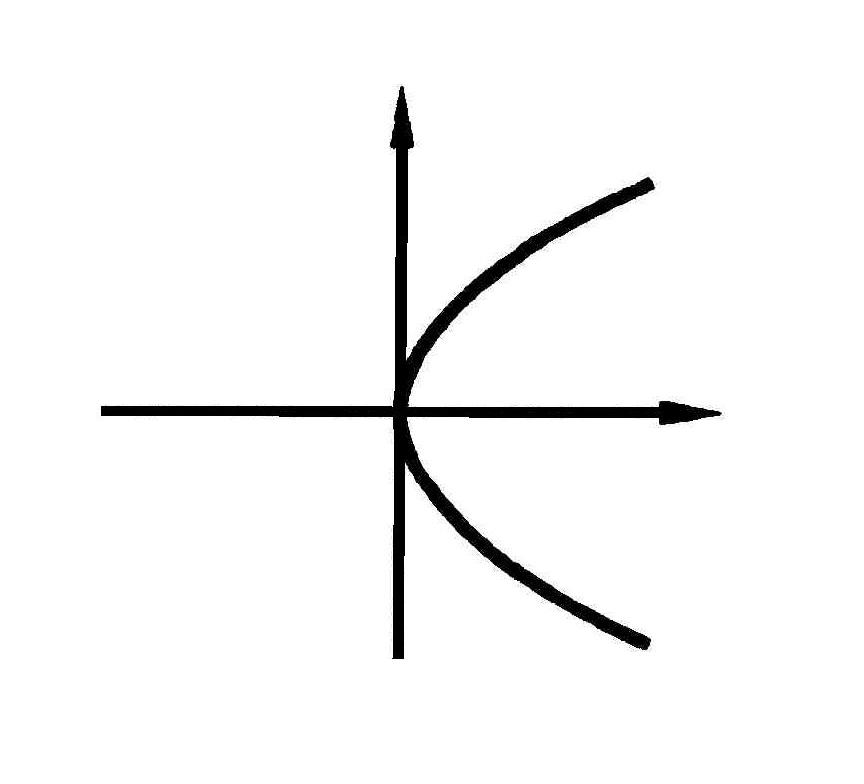
- •Парабола
- •Фокальный радиус точки м(х,y), т.Е. Ее расстояние до фокуса на оси Ох, находится по формуле
- •2. Найти точки пересечения кривых второго порядка
- •Лабораторная работа № 4
- •Основные теоретические сведения, необходимые для выполнения лабораторной работы.
- •1 Построить следующие поверхности второго порядка
- •2 Построить поверхности второго порядка и определить их тип:
- •3 Построить линию пересечения поверхности с плоскостью
- •4 Найти линию пересечения поверхностей второго порядка
- •Приложение б Решение систем линейных алгебраических уравнений методом Гаусса, методом Крамера в среде Mathcad
- •Приложение в Построение кривых второго порядка в среде Mathcad
- •Приложение г Построение поверхностей второго порядка в среде Mathcad
- •Список использованных источников
Основные теоретические сведения, необходимые для выполнения лабораторной работы.
Общее уравнение кривой второго порядка относительно некоторой прямоугольной декартовой системы координат имеет вид:
![]() (3.1)
(3.1)
где
![]()
Существует 9 кривых второго порядка на плоскости.
Приведем
канонические уравнения этих кривых
(![]() ).
).
1)
![]() - уравнение эллипса
- уравнение эллипса
2)
![]() - уравнение гиперболы
- уравнение гиперболы
3)
![]() - уравнение параболы
- уравнение параболы
4)
![]() - мнимый эллипс
- мнимый эллипс
5)
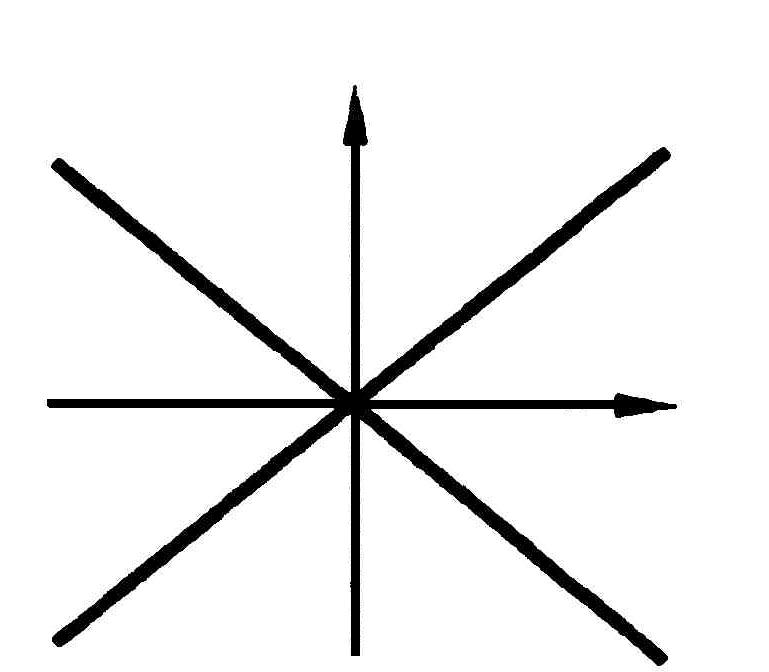
![]() - пара действительных пересекающихся
прямых
- пара действительных пересекающихся
прямых
6)
![]() - пара мнимых пересекающихся прямых
- пара мнимых пересекающихся прямых
7)
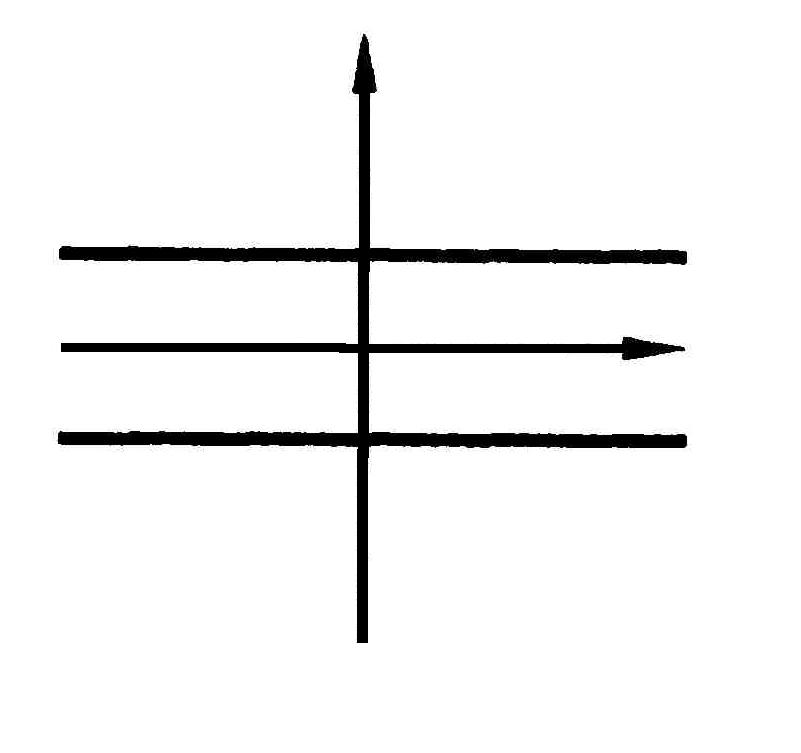
![]() -
пара действительных параллельных прямых
-
пара действительных параллельных прямых
8)
![]() - пара мнимых параллельных прямых
- пара мнимых параллельных прямых
9)
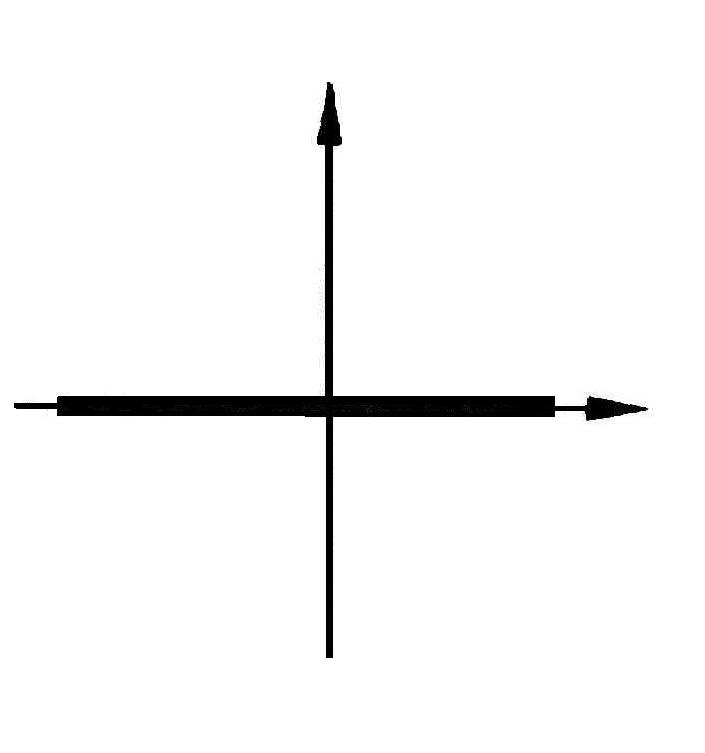
![]() - пара действительных совпавших прямых.
- пара действительных совпавших прямых.
Чтобы определить тип кривой второго порядка достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
Пусть кривая II порядка задана уравнением (3.1). Введем следующие обозначения

Числа
D
и
![]() не зависят от выбора системы координат
на плоскости и называются инвариантами.
не зависят от выбора системы координат
на плоскости и называются инвариантами.
В таблице 1 видно, какому сочетанию знаков определителей D и соответствует та или иная линия второго порядка.
Таблица 1
D |
|
Название |
Вид |
+ |
- |
эллипс |
|
+ |
Мнимый эллипс |
|
|
0 |
Пара мнимых пересекающихся прямых |
|
|
|
|
Гипербола |
|
0 |
Пара действительных пересекающихся прямых |
|
|
0 |
|
Парабола |
|
|
0 |
Пара действительных параллельных прямых |
|
Пара мнимых параллельных прямых |
|
||
Пара действительных совпавших прямых |
|
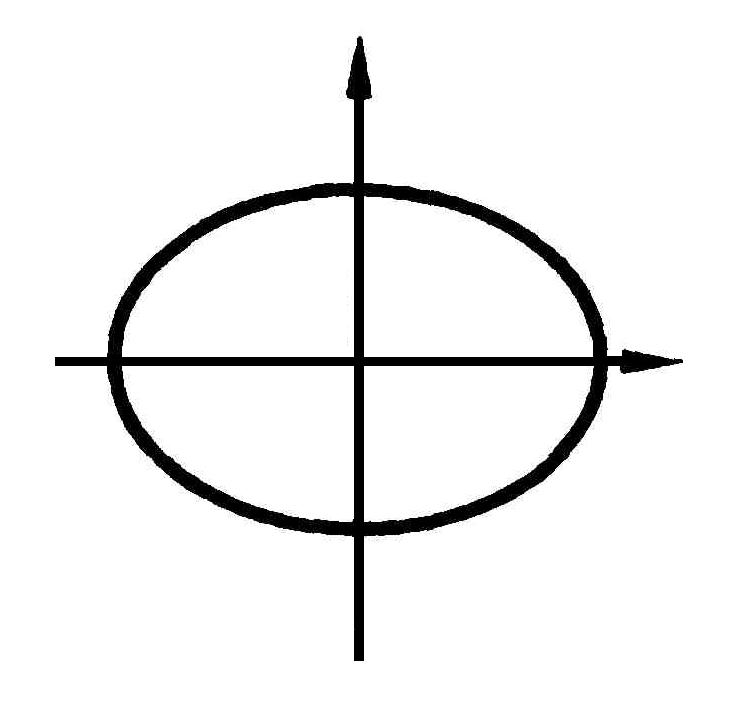
Эллипс
Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть постоянная величина 2а, большая, чем расстояние между фокусами 2с.
Каноническое уравнение эллипса имеет вид
![]()
где
![]() ,
если a>b
и фокусы находятся на оси Ох.
Параметры a
и
b
называются полуосями эллипса.
,
если a>b
и фокусы находятся на оси Ох.
Параметры a
и
b
называются полуосями эллипса.
Отношение
![]() называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
Расстояние точки М(х, y) эллипса до его фокусов (фокальные радиусы) находятся по формулам
![]() .
.
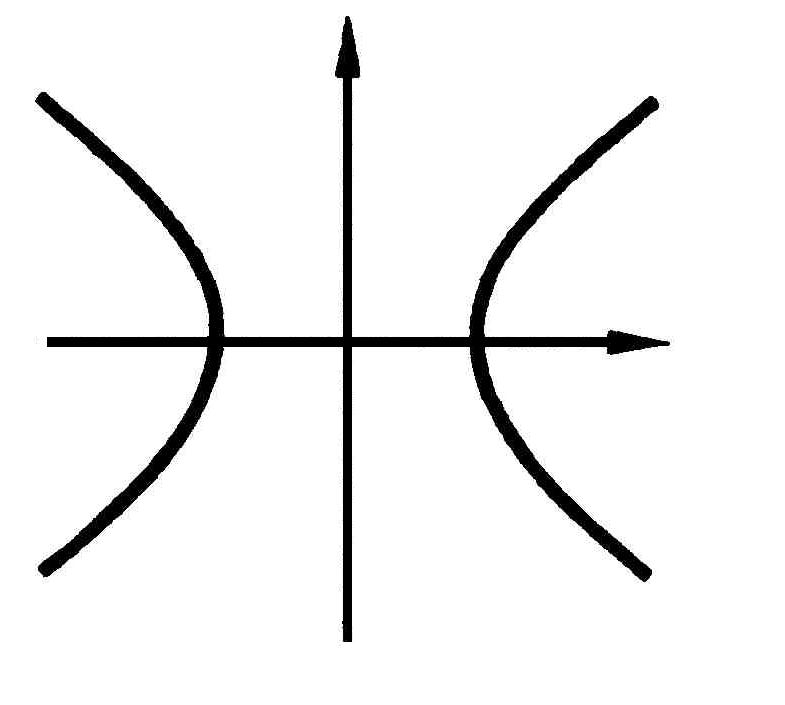
Гипербола
Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина 2а, причем 2a<2c, где 2с – расстояние между фокусами.
Каноническое уравнение гиперболы, симметричной относительно осей координат, имеет вид
![]()
где
![]() .
.
Параметр а называется вещественной полуосью гиперболы и представляет собой расстояние от начала координат до вершины гиперболы, параметр b называется мнимой полуосью.
Эксцентриситетом
гиперболы называется величина
![]() .
.
Расстояния текущей М(х,y) гиперболы до фокусов (фокальные радиусы) определяются по формулам
![]() .
.
Прямые,
заданные уравнениями
![]() ,
являются асимптотами гиперболы.
,
являются асимптотами гиперболы.