3. Матричный метод
Решение
системы
в матричной форме имеет вид:
где
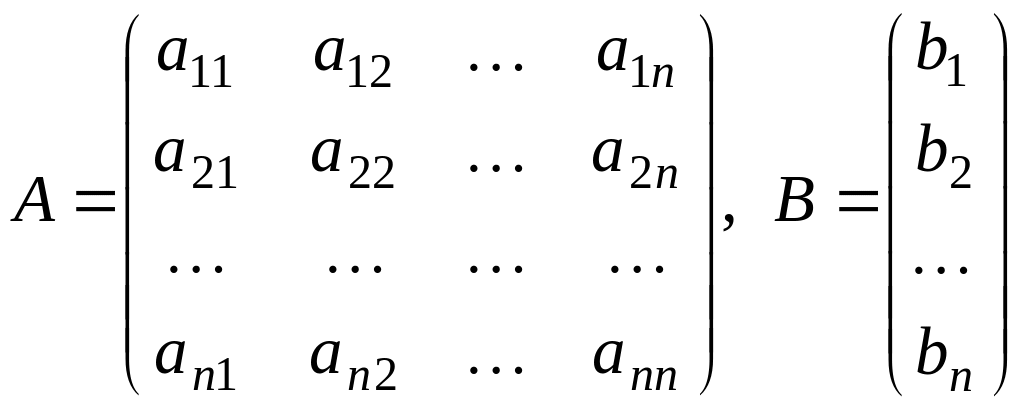
II Решение произвольных систем линейных уравнений
Пусть
дана система
линейных уравнений с
неизвестными
(2.2)
Рассмотрим матрицы
-
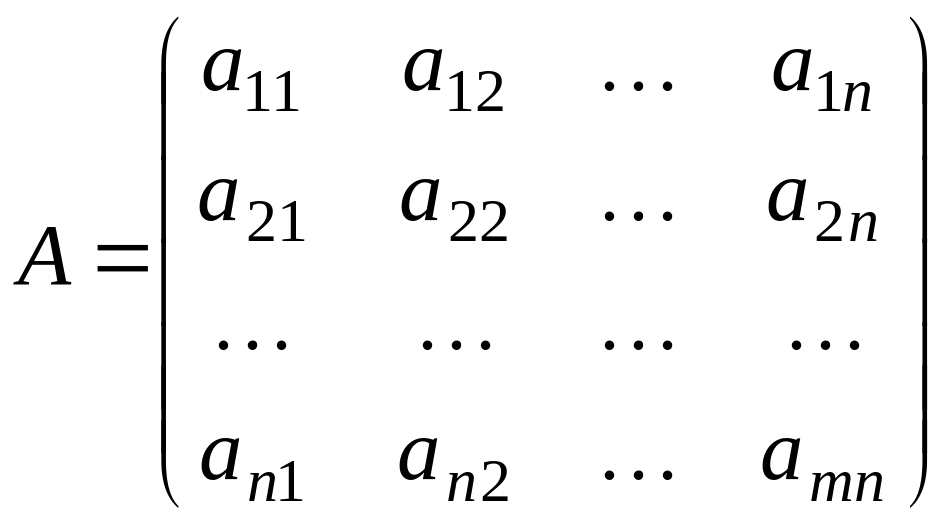основная матрица системы (2.2)
-
расширенная матрица системы (2.2)
Вопрос о совместности системы линейных уравнений (2.2) полностью решается следующей теоремой.
Теорема Кронекера-Капелли: Система линейных уравнений (2.2) тогда и только тогда совместна, когда ранг основной матрицы равен рангу расширенной системы.
Правило решения произвольной системы линейных уравнений.
Пусть дана совместная система линейных уравнений (2.2) и пусть основная матрица А этой системы имеет ранг r. Выбираем в А r линейно независимых строк и оставляем в системе (2.2) лишь уравнения, коэффициенты которых вошли в выбранные строки. В этих уравнениях оставляем в левых частях такие r неизвестных, что определитель из коэффициентов при них отличен от нуля, а остальные неизвестные объявляем свободными и переносим в правые части уравнений. Давая свободным неизвестным произвольные числовые значения и вычисляя значения остальных неизвестных любым из методов, приведенных в пункте 1, мы получим все решения системы (2.2).
Задания для самостоятельного выполнения.
В заданиях данной лабораторной работы N – номер варианта.
Доказать, что система имеет единственное решение и найти его матричным методом:
Исследовать систему на совместность. Если система совместна, то определить, сколько решений она имеет и, в зависимости от этого, найти решение системы или построить общее решение, используя метод Крамера. Сделать проверку.
а)
б)
Исследовать систему на совместность. Если система совместна, то определить, сколько решений она имеет и, в зависимости от этого, найти решение системы методом Гаусса или построить общее решение, используя символьные вычисления системы Mathcad. Сделать проверку.
а)
,
б)
,
в)
.
Доказать, что система имеет ненулевые решения. Найти несколько из них.
Построить фундаментальную систему решений для однородной системы линейных уравнений и сделать проверку полученных результатов.
Найти многочлен пятой степени
,
удовлетворяющий заданным условиям
,
,
,
,
,
.
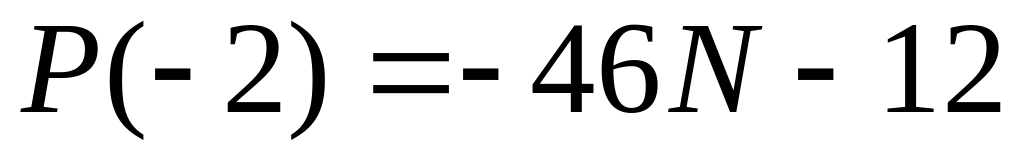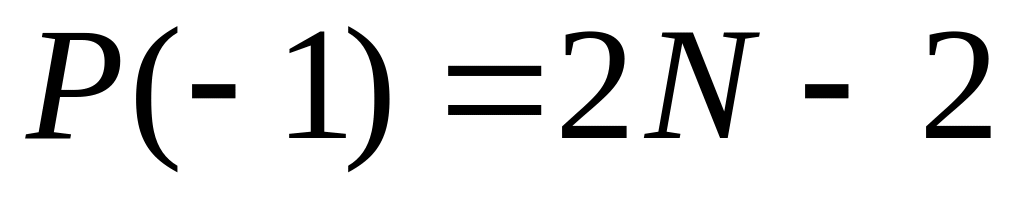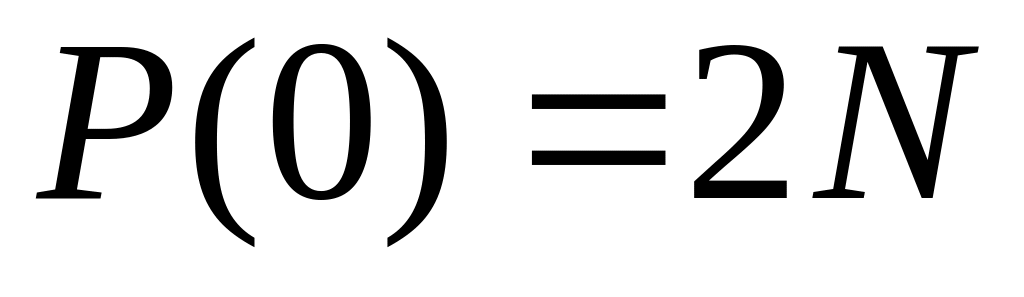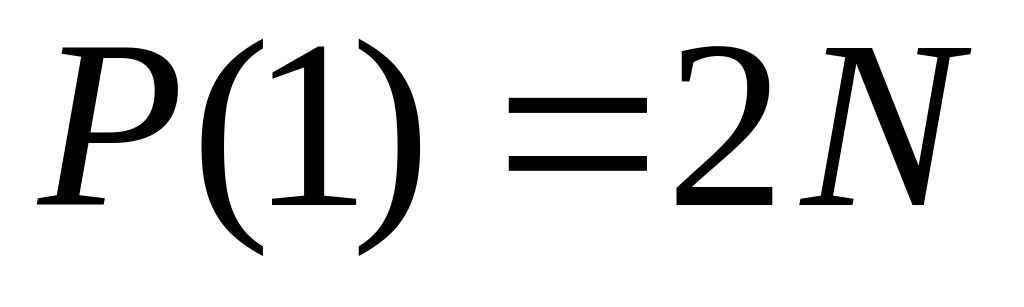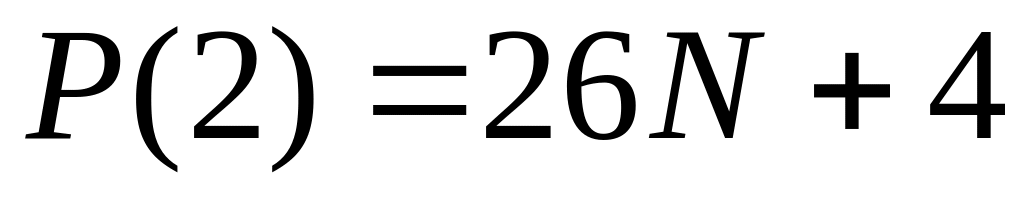Составить математическую модель задачи
и решить её тремя способами (методом
Крамера, Гаусса и матричным).
Лабораторная работа № 3
Тема: Построение кривых второго порядка.
Цель: Рассмотреть возможности построения кривых второго порядка в системе Mathcad
Порядок выполнения работы:
1) Повторить некоторые теоретические сведения, известные из курса аналитической геометрии, необходимые для выполнения работы.
2) Рассмотреть примеры построения кривых второго порядка в Mathcad в Приложении В.
3) Выполнить задачи для самостоятельного решения по вариантам. Вариант соответствует порядковому номеру в журнале.
4) Написать отчет (в свободной форме).