Асимптоты графика функции
Определение.Асимптотой
для кривой
называется
прямая, расстояние до которой до точки,
лежащей на кривой, стремится к нулю при
неограниченном удалении от начала
координат этой точки по кривой, т.е.
.
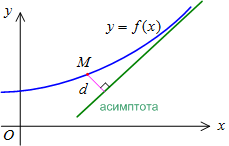
Асимптоты могут быть вертикальными, горизонтальными и наклонными.
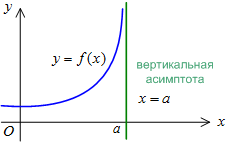
Прямая
является
вертикальной
асимптотой,
если
или,
или
.
Для отыскания вертикальных асимптот необходимо найти те значения , при которых функция неограниченно возрастает или убывает. Обычно это точки разрыва второго рода.
Пример
1.
Найти вертикальные асимптоты графика
функции
.
Решение.
Знаменатель обращается в ноль в точках
.
Так как
и
,
следовательно, прямые
и
являются
вертикальными асимптотами.
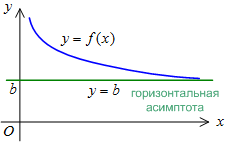
Прямая
является
горизонтальной
асимптотой,
если
.
Для
того, чтобы найти горизонтальную
асимптоту, надо найти предел функции
при
и
.
Пример 2. Найти горизонтальную асимптоту графика функции .
Решение.
Находим предел
.
Следовательно, горизонтальной асимптотой
(причем влево) графика данной функции
при
является
прямая
.
Заметим, что
,
поэтому горизонтальной асимптоты вправо
не существует.
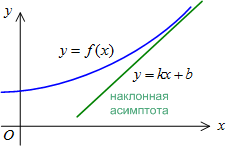
Уравнение
наклонной
асимптоты находится
в виде
,
где
.
Пример
3.
Найти наклонную асимптоту графика
функции
.
Решение.
Находим угловой коэффициент асимптоты:
.
Далее вычисляем свободный член уравнения асимптоты:
.
Таким образом, наклонной асимптотой графика данной функции является прямая .
Вопрос.
Горизонтальной асимптотой графика
функции
является
прямая
Начало формы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общая схема исследования функции и построения графика.
Пустьтребуется исследовать и построить график функции . Для этого нужно:
1.
Найти область определения функции
.
2.
Найти точки пересечения графика функции
с осями координат:
3.
Выяснить, является ли функция четной
(в
этом случае график будет симметричен
относительно оси ординат
)
или нечетной
(график
функции симметричен относительно начала
координат
)
.
4.
Найти
интервалы знакопостоянства функции,
т.е. найти интервалы, где
и
.
5.
Найти асимптоты графика функции
(вертикальные -
и
наклонные
,
где
и
)
.
6.
Найти экстремумы функции (среди
критических точек, в которых
или
не существует), интервалы возрастания
(на них
)
и убывания (на них
).
7.
Найти
точки перегиба (среди критических точек,
в которых
или
не существует) и интервалы выпуклости
функции (
выпукла вниз, если
,
а также
выпукла
вверх, если
).
8. Построить график функции в соответствии с проведенным исследованием. Пример построения графика функции по этому плану будет разобран в соответствующем Практикуме.
Начало формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Начало формы
Конец формы
Конец формы
Начало формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Конец формы
Начало формы
Конец формы