Нахождение наибольшего и наименьшего значения функции на отрезке

Пусть функция непрерывна на отрезке . Такая функция достигает своих наибольшего и наименьшего значений на заданном отрезке. Эти значения функция может принять либо во внутренней точке отрезка (в этом случае эта точка является критической), либо на его границе.

Получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке .

1. Найти критические точки на интервале .

2. Вычислить значения функции в найденных критических точках.

3. Вычислить значения функции на концах отрезка.

4. Среди всех вычисленных значений функции выбрать наибольшее и наименьшее.

Пример. Найти наибольшее и наименьшее значения функции на отрезке .

Решение.

1. Находим критические точки данной функции: .

при . Эта точка принадлежит заданному отрезку .

2. Находим значение функции в критической точке: .

3. Вычисляем значения функции на концах отрезка: . 4. Среди трех значений выбираем наибольшее: , затем наименьшее .

Вопрос. Наименьшее значение функции на отрезке равно

Начало формы

Исследование функции на выпуклость и точки перегиба

График дифференцируемой функции называется выпуклым вниз на интервале , если он расположен выше любой его касательной на этом интервале (рис.13).

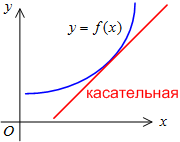
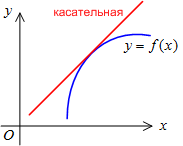
График дифференцируемой функции называется выпуклым вверх на интервале , если он расположен ниже любой его касательной на этом интервале (рис.14).

Точка графика непрерывной функции , отделяющая части различной выпуклости, называется точкой перегиба.

Интервалы выпуклости вверх и вниз находятся с помощью следующей теоремы.

Теорема 1. Если функция во всех точках интервала имеет отрицательную вторую производную, то есть , то график функции на этом интервале является выпуклым вверх. Если во всех точках интервала, то график функции является выпуклым вниз.

Для нахождения точек перегиба функции используется следующая теорема.

Теорема 2. Достаточное условие точки перегиба. Если вторая производная функции при переходе через точку , в которой вторая производная равна нулю или не существует, меняет знак, то точка графика с абсциссой является точкой перегиба.

Пример. Исследовать на выпуклость и точки перегиба график функции .

Решение. Находим, что .

Вторая производная существует на всей числовой оси. Найдем точку, в которой она равна нулю: .

При получим , при имеем , следовательно, на интервале график функции является выпуклым вверх,

на интервале график является выпуклым вниз, поэтому точка с абсциссой является точкой перегиба.

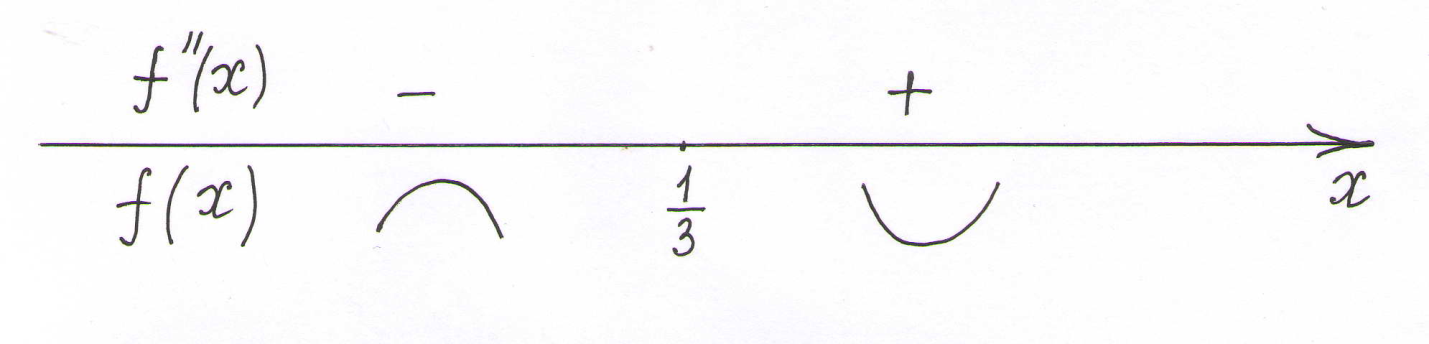
Вопрос. Сколько точек перегиба имеет график функции ?

Начало формы

	ни одной