Разложение элементарных функций по формуле Тейлора

Найдем разложение функции по формуле Тейлора в окрестности точки . Находя последовательно производные от этой функции, получим:

,

,

,

.

Находим значение

Подставим полученные значения в формулу Тейлора:

,

где - остаточный член в форме Лагранжа.

При получим формулу, позволяющую найти приближенное значение числа :

.

Так как , , то при и получим

Если задана погрешность , то подберем таким образом, чтобы .

.

Таким образом, .

Найдем разложение функции в окрестности точки по формуле Тейлора:

,

,

,

,

.

Таким образом, все производные четного порядка в точке равны нулю, а производные нечетного порядка равны или . Следовательно, разложение примет вид:

,

где остаточный член в форме Лагранжа равен .

Используя полученное разложение, приближенно вычислим . При вычислении ограничимся первыми двумя членами разложения:

.

Приведем разложения по формуле Тейлора в окрестности точки некоторых элементарных функций:

.

.

.

Формулу Тейлора при также называют формулой Макларена.

Вопрос. Разложение какой функции в окрестности точки имеет вид

?

Начало формы

Исследование функции на монотонность

Пусть функция определена на множестве и пусть множество принадлежит множеству . Если для любых значений из неравенства вытекает неравенство:

1. , то функция называется возрастающей на множестве ;

2. , то функция называется неубывающей на множестве ;

3. , то функция называется убывающей на множестве ;

4. , то функция называется невозрастающей на множестве .

Возрастающие, убывающие, невозрастающие и неубывающие функции на множестве называются монотонными на этом множестве, а возрастающие и убывающие - строго монотонными.

Достаточные условия возрастания и убывания функции: Если функция дифференцируема на интервале  и для любых , то эта функция возрастает (убывает) на заданном интервале.

<!--[endif]-->

Если для любых , то функция не убывает (не возрастает) на этом интервале.

Пример. Найти интервалы возрастания и убывания функции .

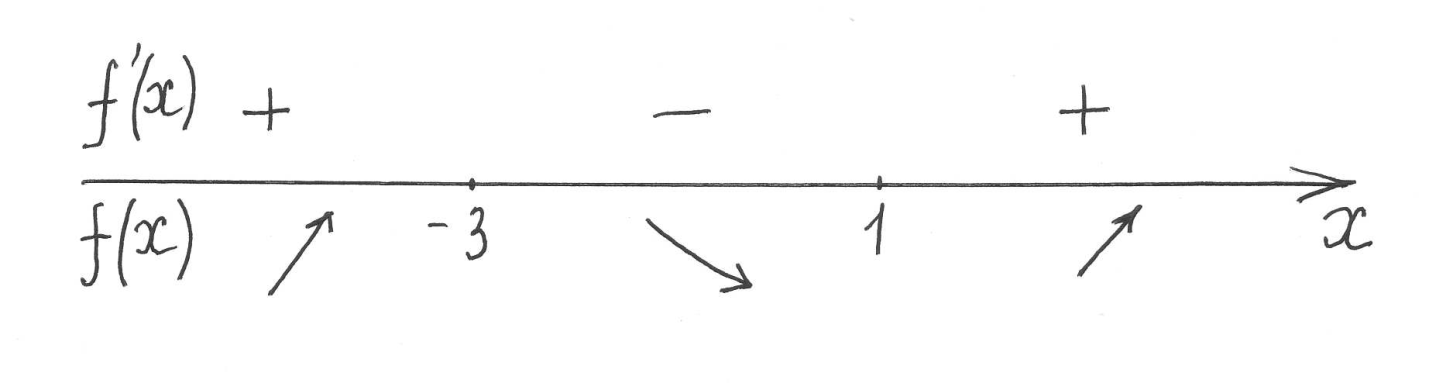
Решение. Область определения функции – вся числовая прямая. Находим производную функции . Методом интервалов находим интервалы знакопостоянства производной.

Из неравенства следует, что функция возрастает при всех значениях ;

а из неравенства следует, что функция убывает на интервале .

Вопрос. Функция возрастает на интервале:

Начало формы