Теорема Лагранжа

Теорема. Пусть функция непрерывна на отрезке и дифференцируема на интервале . Тогда на интервале найдется такая точка , что

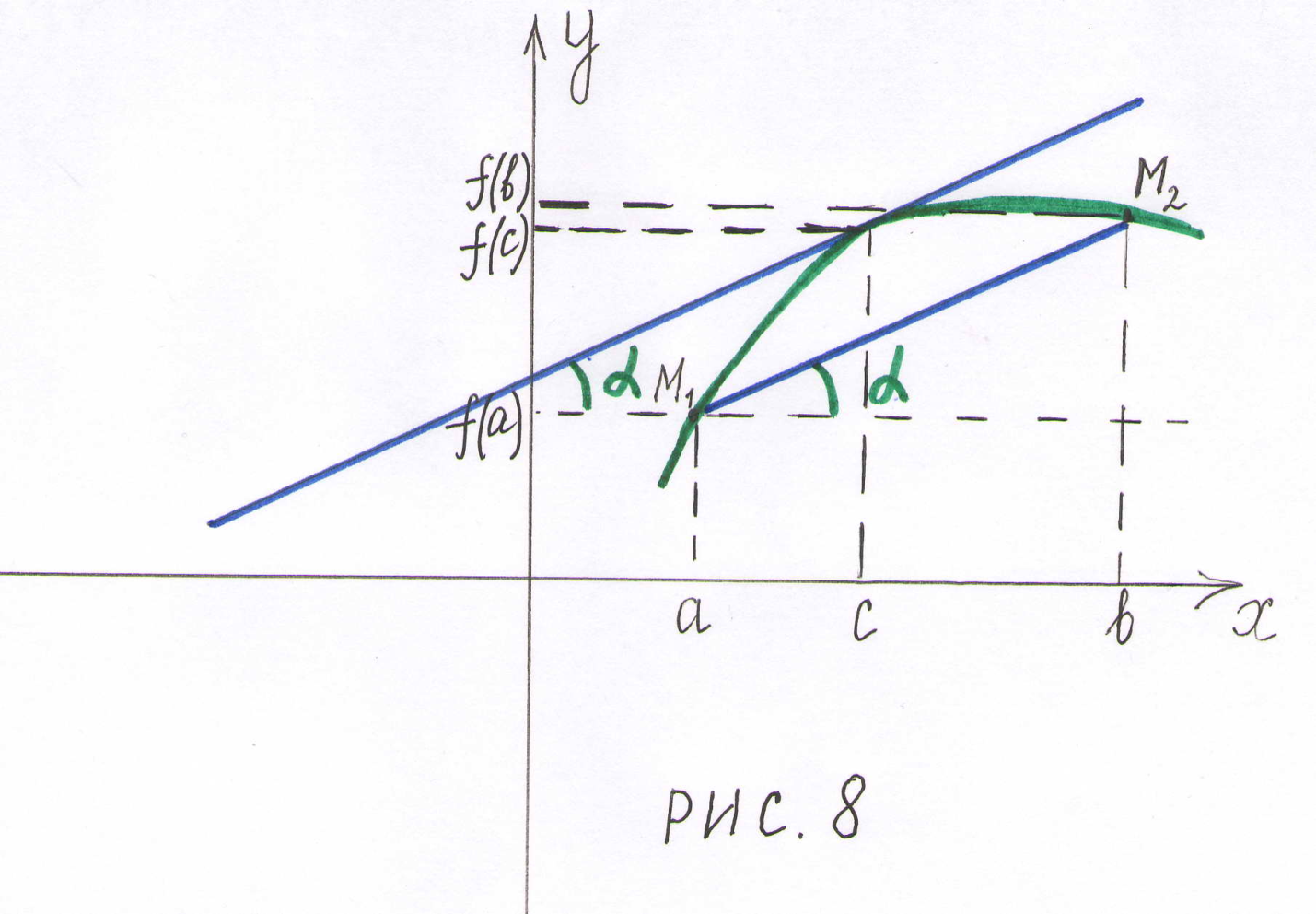
Выясним геометрический смысл теоремы Лагранжа. Величина есть угловой коэффициент прямой, проходящей через точки , принадлежащие графику функции . Из теоремы Лагранжа следует, что существует такая точка такая, что касательная к графику функции в точке параллельна данной прямой. Таких точек может быть несколько, но, по крайней мере, одна всегда существует (рис. 8).

Пример 1. Проверить, что функция удовлетворяет условиям теоремы Лагранжа на отрезке , и найти точку .

Решение. Так как данная функция непрерывна на отрезке и дифференцируема во всех внутренних точках этого отрезка, то она удовлетворяет условиям теоремы Лагранжа. Следовательно, внутри этого отрезка существует точка, удовлетворяющая равенству:

.

Так как , следовательно , то есть .

Пусть функция удовлетворяет условиям теоремы Лагранжа на отрезке , а точки и принадлежат этому отрезку. Тогда функция удовлетворяет условиям теоремы Лагранжа на отрезке и существует точка , принадлежащая интервалу , такая, что выполняется равенство

.

Эта формула называется формулой конечных приращений Лагранжа.

Следствие 1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.

Следствие 2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.

Теорема Коши

Теорема. Пусть функции и непрерывны на отрезке и дифференцируемы на интервале , причем для всех . Тогда найдется такая точка на этом интервале, что

.

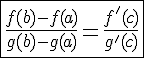Эта формула называется формулой Коши или обобщенной формулой конечных приращений. Теорема Лагранжа является частным случаем теоремы Коши, если .

Правило Лопиталя

Правило Лопиталя – это простой и весьма эффективный способ раскрытия неопределенностей, используемый для вычисления пределов функций.

Следующая теорема дает правило раскрытия неопределенности вида .

Теорема 1. Пусть функции и определены и дифференцируемы в окрестности точки , за исключением, может быть, самой точки . Пусть также , где в указанной окрестности точки . Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел , причем справедлива формула:

.

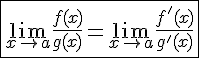Пример 1. Найти предел, пользуясь правилом Лопиталя: .

Решение. Функции и стремятся к нулю при , причем в окрестности точки . Применяя правило Лопиталя, получим:

Вторая теорема Лопиталя позволяет раскрывать неопределенности вида .

Теорема 2. Пусть функции определены и дифференцируемы в некоторой окрестности точки , за исключением, может быть, самой этой точки. Пусть и в окрестности точки . Тогда, если существует предел отношения производных ( конечный или бесконечный ), то существует и предел , причем справедлива формула

.

Если отношение в свою очередь опять представляет собой неопределенность вида или , то правило Лопиталя можно применять второй раз и т.д.

Пример 2. Найти предел, применяя правило Лопиталя: .

Решение.

.

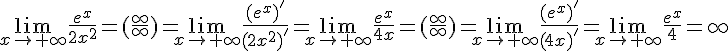При вычислении этого предела правило Лопиталя применялось дважды.

Кроме неопределенностей вида и правило Лопиталя применяется для раскрытия неопределенностей следующих видов:

.

Неопределенности вида , можно свести к неопределенностям вида или , а затем раскрыть их с помощью правила Лопиталя.

Пример 3. Найти предел функции, применяя правило Лопиталя: .

Решение.

.

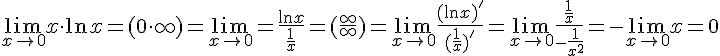При решении этого примера неопределенность вида была сведена к неопределенности вида .

Пример 4. Найти предел функции, применяя правило Лопиталя: .

Решение. В этом примере имеем неопределенность вида . Вычислим этот предел, используя основное логарифмическое тождество:

. (См. предыдущий пример).

Вопрос. После применения правила Лопиталя предел функции преобразуется к виду

Начало формы

Формула Тейлора

Английский математик Брук Тейлор в 1717 году сделал замечательное открытие. Он вывел одну из главных формул математического анализа, имеющую применения в разных областях науки. Тейлор выяснил, что любую дифференцируемую в окрестности некоторой точки функцию с достаточной степенью точности можно заменить многочленом.

Формула Тейлора.Пусть функция имеет в окрестности точки конечные производные до порядка включительно. Тогда для любой точки из этой окрестности имеет место формула:

.

Эта формула называется формулой Тейлора с остаточным членом в форме Лагранжа. Остаточный член (последнее слагаемое в данной формуле) определяет степень точности, с которой можно заменить функцию соответствующим многочленом.

Формула Тейлора также может быть записана в виде:

, где

- многочлен Тейлора,

, - остаточный член формулы Тейлора, записанный в форме Лагранжа. есть погрешность приближенного равенства .

Остаточный член может быть записан в форме Пеано, в этом случае при . Такая запись означает, что остаточный член является величиной бесконечно малой более высокого порядка, чем .

Иногда многочлен Тейлора записывают с помощью дифференциалов функции :

Таким образом, формула Тейлора дает возможность заменить функцию в окрестности точки многочленом с точностью, равной значению остаточного члена .