- •Задачи, приводящие к понятию производной
- •Определение производной функции и её обозначения
- •Механический, физический и геометрический смысл производной
- •Логарифмическое дифференцирование
- •Теорема Лагранжа
- •Теорема Коши
- •Правило Лопиталя
- •Разложение элементарных функций по формуле Тейлора
- •Исследование функции на монотонность
- •Исследование функций на экстремум
- •Нахождение наибольшего и наименьшего значения функции на отрезке
- •Исследование функции на выпуклость и точки перегиба
- •Асимптоты графика функции
- •Общая схема исследования функции и построения графика.
Логарифмическое дифференцирование
Рассмотрим
сложную функцию
![]() ,
где
,
где
![]() .
Найдем производную этой функции по
переменной
.
.
Найдем производную этой функции по
переменной
.
![]() .
.
Или
![]() .
.
Производная
функции
![]() называется
логарифмической производной функции
.
Логарифмическая производная применяется
при вычислении производных
показательно-степенных функций.
называется
логарифмической производной функции
.
Логарифмическая производная применяется
при вычислении производных
показательно-степенных функций.
Определение.
Показательно-степенной
функцией
называется функция вида
![]() ,
где
,
где
![]() и
и
![]() –
функции от переменной
.
–
функции от переменной
.
Примеры
показательно-степенных функций:
![]() ,
,
![]() ,
,
![]() .
.
Найдем производную показательно-степенной функции . Предварительно прологарифмируем правую и левую части уравнения.
![]() .
.
![]()
(при
этом использовали свойство логарифмов
![]() )
)
Дифференцируем
обе части по переменной
,
при этом считаем функцию
![]() сложной
функцией:
сложной
функцией:
![]() ,
,
![]() .
.
Выражаем и, учитывая, что , получаем формулу для вычисления производной показательно-степенной функции:
 .
.
Пример.
Вычислить производную показательно-степенной
функции
![]() .
.
Решение.
Логарифмируем
обе части уравнения:
![]() ,
затем преобразовываем равенство,
используя свойство логарифмов:
,
затем преобразовываем равенство,
используя свойство логарифмов:
![]() ,и
дифференцируем обе части по переменной
:
,и
дифференцируем обе части по переменной
:
![]() .
.
В
левой части вычисляем логарифмическую
производную функции
![]() ,
а в правой части находим производную
произведения двух функций. Поэтому:
,
а в правой части находим производную
произведения двух функций. Поэтому:
![]() ,
,
![]() .
.
Выражая
и
учитывая, что
![]() ,
получаем производную исходной функции:
,
получаем производную исходной функции:
![]() .
.
Вопрос.
Производная функции
![]() имеет
вид:
имеет
вид:
Начало формы
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Производная обратной функции
Теорема.Если
функция
строго
монотонна на интервале
Пример.
Рассмотрим функцию
Решение.
Пользуясь правилом дифференцирования
обратной функции, найдем производную
.
Функция, обратная к исходной, имеет
вид:
Получили,
что
Вопрос.
Дана функция
Начало формы
1/ey+2y Конец формы
Дифференцируемость функции. Связь между непрерывностью и дифференцируемостью функции Пусть функция имеет в точке отличную от нуля производную, то есть
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
или
Таким
образом, приращение функции
представляет
собой сумму двух слагаемых
Определение
1. Функция
называется
дифференцируемой
в точке
где
Понятия дифференцируемости функции в точке и существования производной в этой же точке тесно связаны между собой. Для функции одной переменной эти понятия являются равносильными.
Теорема 1.Для того чтобы функция , была дифференцируема в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Определение
2. Функция
называется
дифференцируемой
на отрезке
Теорема 2. Если функция дифференцируема в некоторой точке , то она непрерывна в этой точке. Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, то есть не иметь конечной производной в этой точке. В точках разрыва (точках, в которых функция не является непрерывной) функция не может иметь производную, поэтому в таких точках функция не дифференцируема.
Пример
1.
Функция
Пример
2.
Функция
Следовательно, в точке функция является непрерывной, но не дифференцируемой.
Вопрос. Какая из этих функций не дифференцируема в точке ? Начало формы
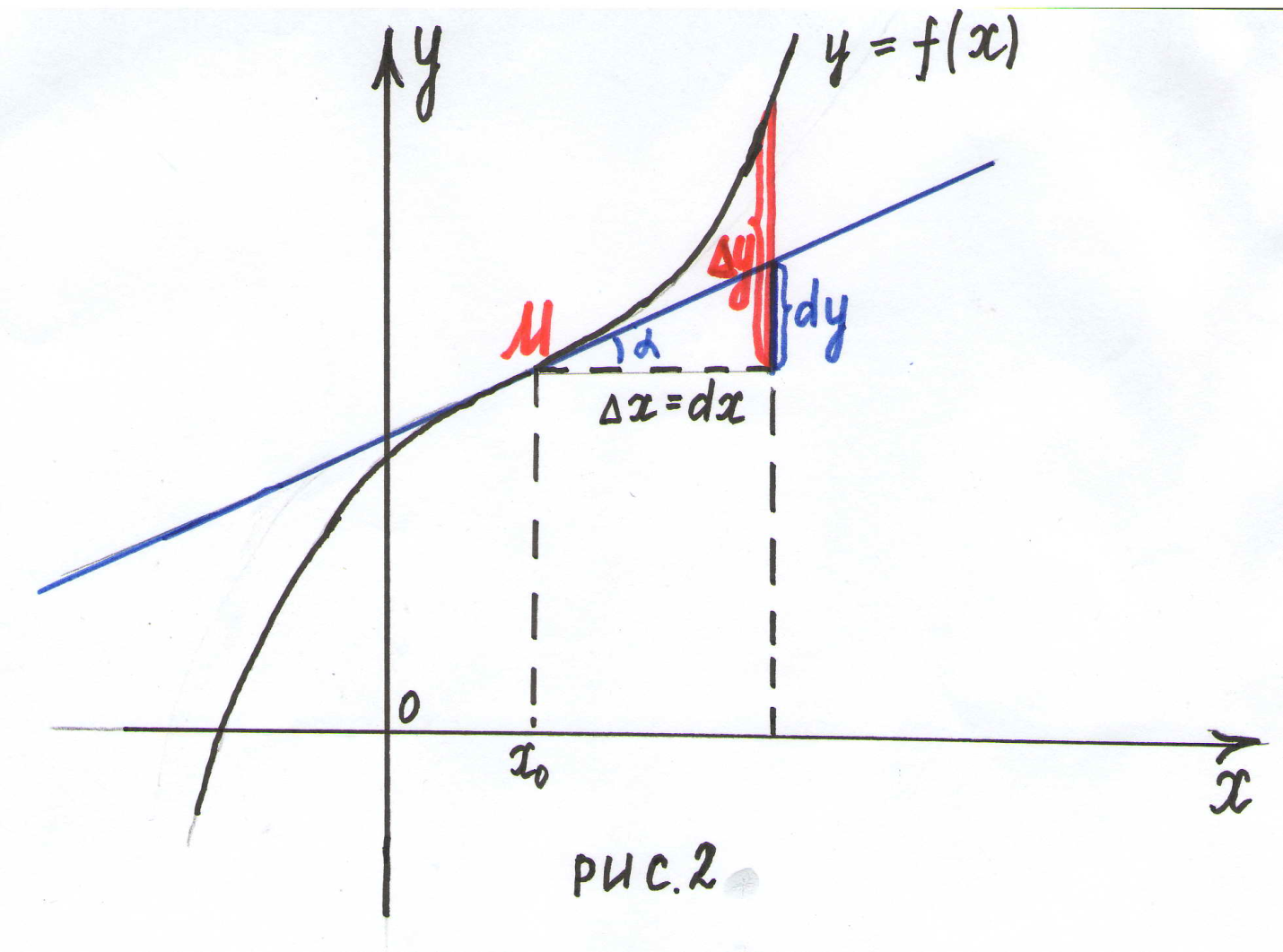
Определение дифференциала функции Пусть функция дифференцируема в точке , то есть ее приращение можно записать в виде: , где при , .
Первое
слагаемое
Определение.
Дифференциалом
функции
в
точке
называется
главная, линейная относительно
часть
приращения функции
и
обозначается
Дифференциалом
независимой переменной
называется
приращение этой переменной
Пример.
Вычислите
дифференциал функции
Решение.
Так как дифференциал функции равен
произведению производной этой функции
на дифференциал аргумента, то
Инвариантность формы первого дифференциала Пусть даны две дифференцируемые функции и , образующие сложную функцию . По теореме о производной сложной функции можно написать:
Умножив
обе части этого равенства на
Но
Таким образом, первый дифференциал функции определяется одной и той же формулой независимо от того, является ли её аргумент независимой переменной или является функцией другого аргумента. Это свойство дифференциала называется инвариантностью (неизменностью) формы первого дифференциала.
Вопрос.
Дифференциал
Начало формы
Приближенные вычисления с помощью дифференциала Как можно заметить из предыдущей задачи, погрешность при замене на небольшая. Во многих случаях ее можно считать малой по сравнению с приращением функции. Поэтому в приближенных вычислениях часто пользуются приближенным равенством
из которого получается формула для приближенных вычислений с помощью дифференциала функции:
Пример.
Вычислить приближенно
Решение. По формуле для приближенных вычислений имеем:
Тогда
Вопрос.
Значение
Начало формы
Конец формы Конец формы Конец формы
|
Производные высших порядков
Пусть функция дифференцируема на некотором отрезке . Производная этой функции представляет собой также функцию от переменной . Дифференцируя эту функцию, получаем вторую производную от функции .
Производная
от первой производной называется
производной
второго порядка
или второй производной от первоначальной
функции и обозначается символом
![]() или
или
![]() :
:
![]() .
.
Выражение читается как "игрек два штриха".
Так,
например, если
![]() ,
то
,
то
![]() ,
,
![]() .
.
Производная
от второй производной называется
производной
третьего порядка
или третьей производной и обозначается
![]() или
или
![]() (читается
"эф
три штриха от икс").
(читается
"эф
три штриха от икс").
Производная
от производной третьего порядка
называется производной
четвертого порядка
или четвертой производной и так далее.
Начиная с четвертой производные могут
обозначаются римскими цифрами:
![]() ,
,
![]() и
т.д.
и
т.д.
Производная
![]() -порядка
обозначается символом
-порядка
обозначается символом
![]() или
или
![]() ,
а вычисляется по формуле
,
а вычисляется по формуле

Правила дифференцирования производных высших порядков следующие:
![]() .
.
![]() .
.
Пример:
Вычислите производные
![]() для
функции
для
функции
![]() .
.
Решение:
![]() .
.
![]()
![]() .
.
Вопрос.
Производная четвертого порядка для
функции
![]() равна
равна
Начало формы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дифференциалы высших порядков
Пусть
дана функция
,
дифференциал этой функции
![]() есть
некоторая функция от
,
при этом будем считать, что от
зависит
только
,
приращение аргумента
от
самого значения аргумента не зависит.
есть
некоторая функция от
,
при этом будем считать, что от
зависит
только
,
приращение аргумента
от
самого значения аргумента не зависит.
Дифференциал
от дифференциала функции называется
вторым
дифференциалом
или дифференциалом второго порядка
этой функции и обозначается
![]() .
В силу определения дифференциала имеем:
.
В силу определения дифференциала имеем:
![]() .
.
Так как от не зависит, то при дифференцировании выносится за знак производной:
![]() .
.
Принята
также запись дифференциала без скобок:
![]() .
.
Третьим дифференциалом или дифференциалом третьего порядка называется дифференциал от второго дифференциала и так далее:
![]() ,
...
,
...
![]() .
.
Пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциала функции соответствующего порядка к дифференциалу аргумента, возведенного в такую же степень:
![]() .
.
Вопрос.
Выберите правильное обозначение второго
дифференциала функции
![]() :
:
Начало формы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная функций, заданных в параметрическом виде
Даны два уравнения:
![]() ,
,
где
каждому значению
соответствует
по одному значению
и
.
Если рассматривать значения
и
как
координаты точки на координатной
плоскости
![]() ,
то каждому значению
,
будет соответствовать определенная
точка плоскости. Когда
изменяется
от
,
то каждому значению
,
будет соответствовать определенная
точка плоскости. Когда
изменяется
от
![]() до
до
![]() ,
то эта точка на плоскости описывает
некоторую кривую. Уравнения:
,
то эта точка на плоскости описывает
некоторую кривую. Уравнения:
![]()
называется параметрическим уравнением этой кривой, называется параметром, а способ задания кривой этими уравнениями называется параметрическим.
Пример.
Дана
окружность с центром в начале координат
и радиусом
![]() (рис.
3).
(рис.
3).
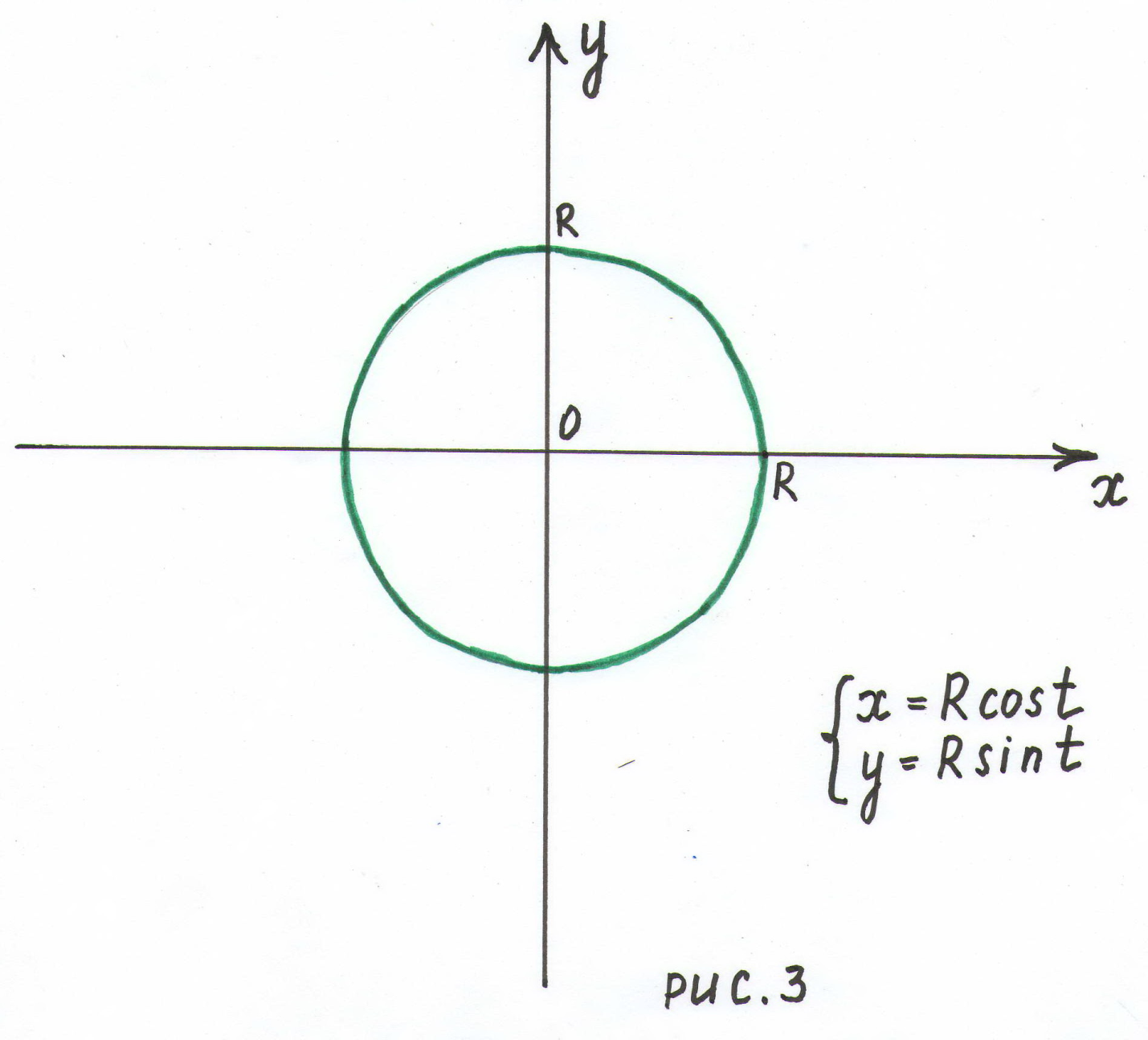
Пусть - это угол, образованный радиусом этой окружности, и осью . Тогда координаты любой точки окружности выражаются через параметр следующим образом:
![]()
Причем
изменяется
от 0 до
![]() .
Это и есть параметрическое уравнение
окружности. Возводя в квадрат оба
уравнения и складывая их, получаем
каноническое уравнение окружности:
.
Это и есть параметрическое уравнение
окружности. Возводя в квадрат оба
уравнения и складывая их, получаем
каноническое уравнение окружности:
![]() .
.
Для того чтобы найти производную функции, заданной в параметрическом виде, используется формула:
 или
или
 .
.
Для нахождения второй производной параметрической функции используется следующая формула:
 .
.
Пример.
Функция задана параметрическим
уравнением:
![]()
![]() .
.
Найти
производную функции
при
любом значении параметра tи
при
![]() .
Найти угловой коэффициент касательной
в точке, соответствующей значению
параметра
.
Найти угловой коэффициент касательной
в точке, соответствующей значению
параметра
![]() .
.
Решение.
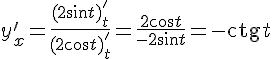 -
производная заданной функции при любом
значении параметра
.
-
производная заданной функции при любом
значении параметра
.
Находим значение производной при :
![]()
Угловой
коэффициент касательной в точке,
соответствующей значению параметра
,
равен значению производной при
.
Следовательно,
![]() .
Так как угловой коэффициент касательной
равен нулю, то касательная, проведенная
к окружности в этой точке, параллельна
оси
.
.
Так как угловой коэффициент касательной
равен нулю, то касательная, проведенная
к окружности в этой точке, параллельна
оси
.
Вопрос.
Производная
функции,
заданной параметрическим уравнением
![]() ,
равна:
,
равна:
Начало формы
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Теорема о корнях уравнения (теорема Ролля)
Теорема.
Пусть функция
непрерывна
на отрезке
,
дифференцируема на интервале
![]() и
принимает на концах отрезка равные
значения
и
принимает на концах отрезка равные
значения
![]() .
Тогда существует по крайней мере одна
точка
.
Тогда существует по крайней мере одна
точка
![]() на
интервале
,
для
которой
на
интервале
,
для
которой
![]() .
.
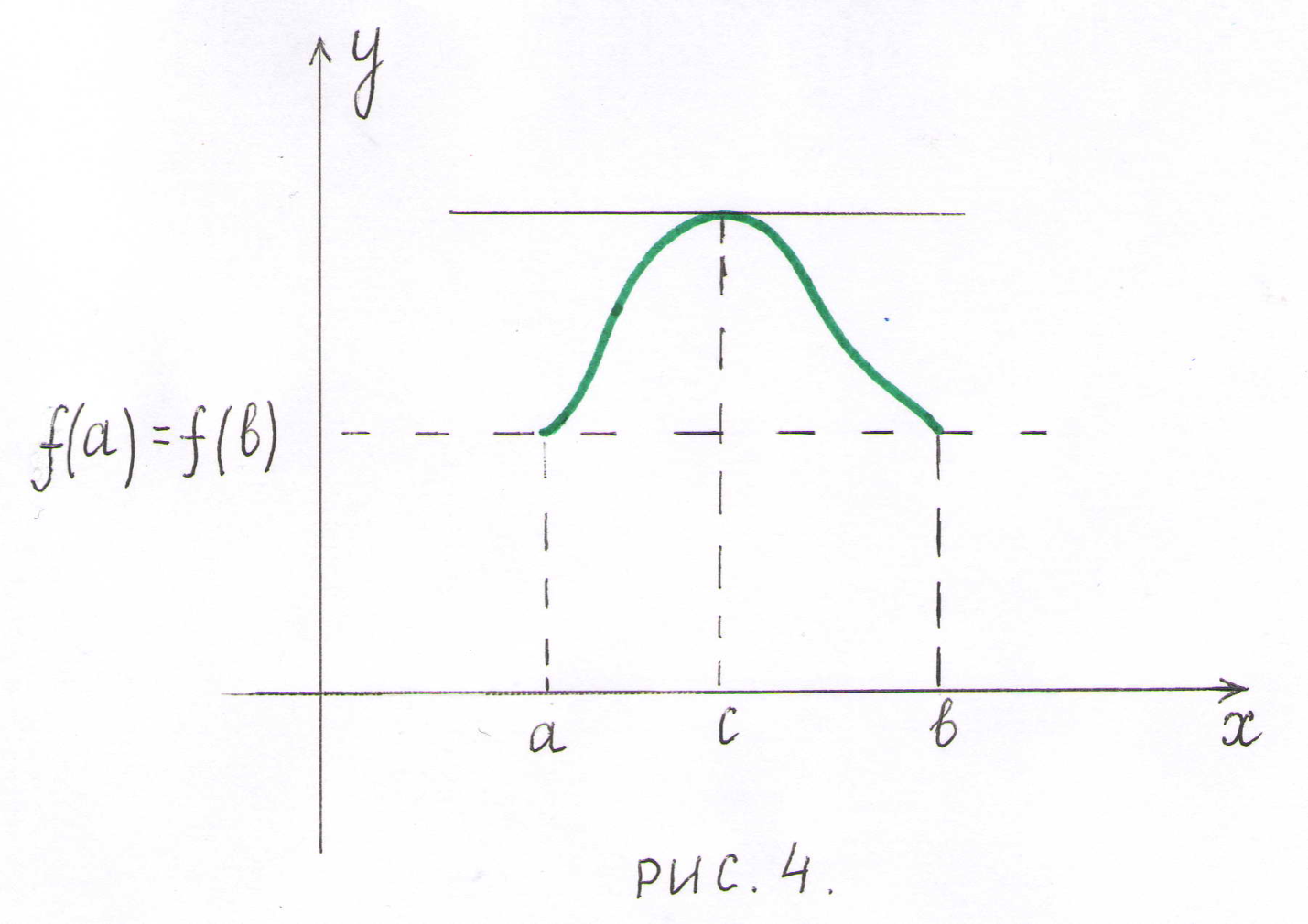
Геометрически
теорема Ролля означает, что у графика
непрерывной на отрезке
и
дифференцируемой внутри него функции,
принимающей на концах этого отрезка
равные значения, существует хотя бы
одна точка
![]() ,
в которой касательная параллельна оси
абсцисс (рис.4).
,
в которой касательная параллельна оси
абсцисс (рис.4).
Пример
1.
Необходимо проверить, справедлива ли
терема Ролля для функции
![]() на
отрезке
на
отрезке
![]() ,
и найти соответствующее значение
.
,
и найти соответствующее значение
.
Решение.
Функция непрерывна на этом отрезке и
дифференцируема на интервале
![]() .
Кроме того,
.
Кроме того,
![]() ,
поэтому теорема Ролля для данной функции
на данном отрезке справедлива. Найдем
значение
,
для
которого
,
поэтому теорема Ролля для данной функции
на данном отрезке справедлива. Найдем
значение
,
для
которого
![]() ,
из уравнения
,
из уравнения
![]() ,
то есть
,
то есть
![]() .
Поскольку найденная точка принадлежит
интервалу
.
Поскольку найденная точка принадлежит
интервалу
![]() ,
то
,
то
![]() -
искомое значение. Касательная, проведенная
к графику функции в этой точке, параллельна
оси абсцисс (рис.5).
-
искомое значение. Касательная, проведенная
к графику функции в этой точке, параллельна
оси абсцисс (рис.5).
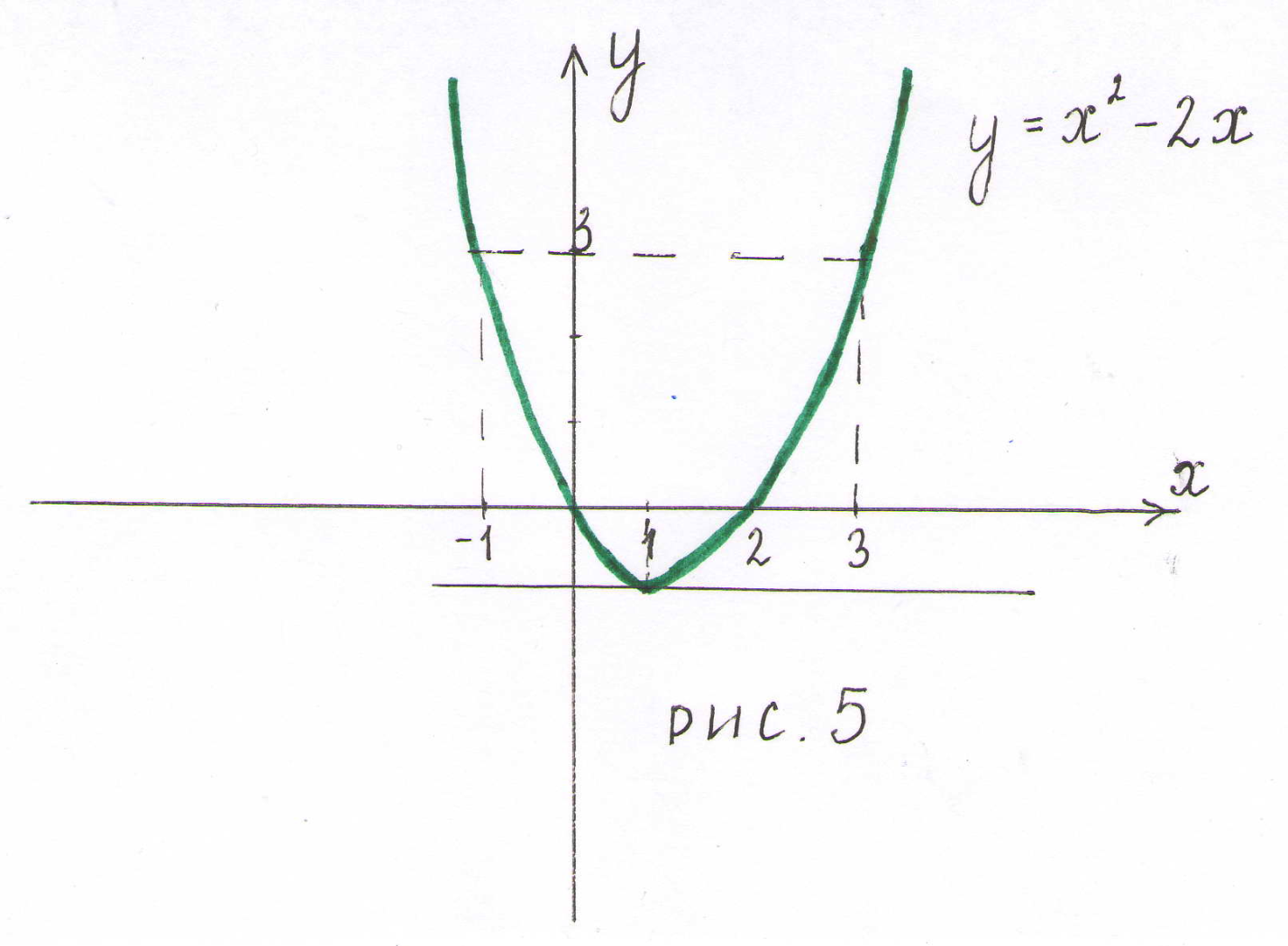
Пример
2. Проверить,
справедлива ли теорема Ролля на отрезке
![]() для
функций
для
функций
![]() и
и
![]() .
.
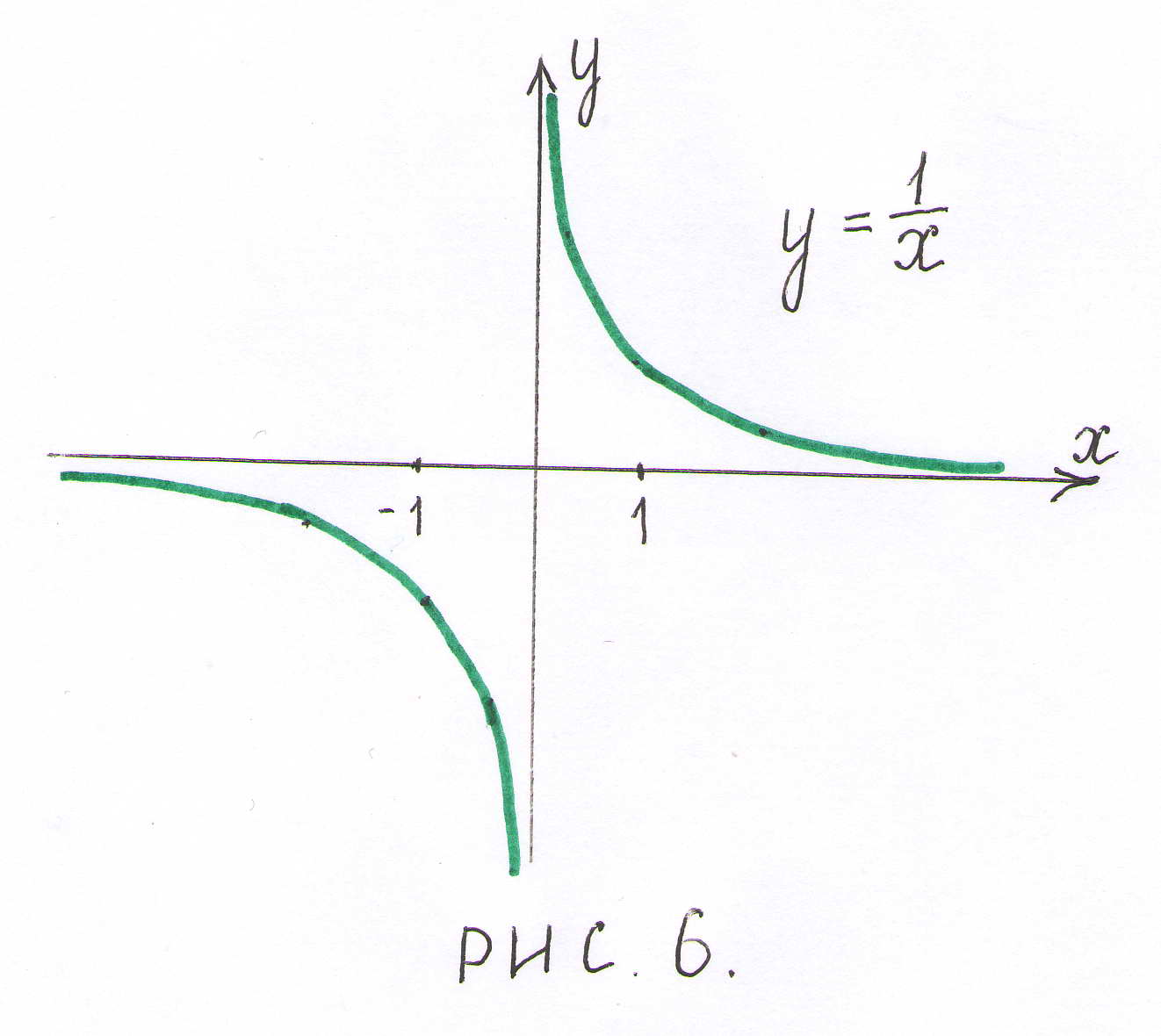
Решение. Функция имеет точку разрыва в точке , принадлежащую заданному отрезку, поэтому на этом отрезке она не удовлетворяет теореме Ролля (рис.6).
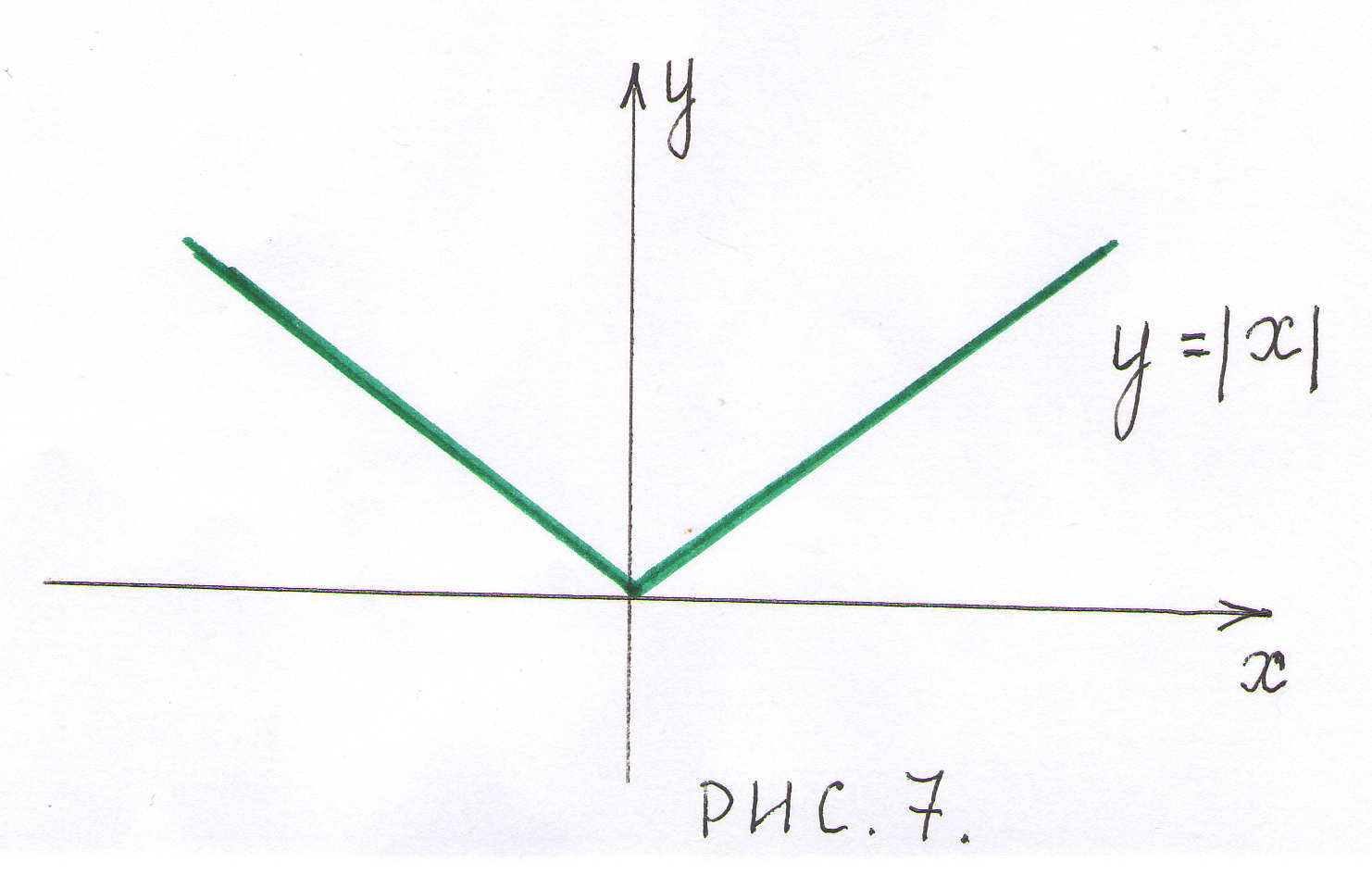
Рассмотрим на этом же отрезке функцию . Эта функция непрерывна на отрезке и принимает на концах отрезка равные значения, но в точке она не дифференцируема, поэтому она не удовлетворяет теореме Ролля на заданном отрезке (рис.7).
Вопрос.
Какая
функция удовлетворяет теореме Ролля
на отрезке
![]() ?
?
Начало формы
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 или
или
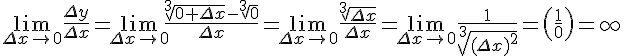 .
.