МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИННОВАЦИОННЫХ ТЕХНОЛОГИЙ И ПРЕДПРИНИМАТЕЛЬСТВА

З А Д А Ч Н И К К У Ч Е Б Н И К У

«ПРОГНОЗИРОВАНИЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ»

Раздел I. Прогнозирование на основе регрессионных моделей

1. Парная регрессия и корреляция

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

В настоящее время под регрессией понимается функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной, которая строится с целью предсказания (прогнозирования) этого среднего значения при фиксированных значениях первых.

Парная регрессия – уравнение связи двух переменных y и x: y= , где y - зависимая переменная (результативный признак);

x - незавасимая, объясняющая переменная (признак-фактор).

Если функция регрессии линейна, то говорят о линейной регрессии: .

Нелинейные регрессии делятся на: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

• полиномы разных степеней

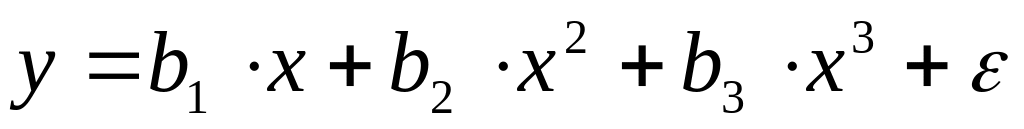
• равносторонняя гипербола

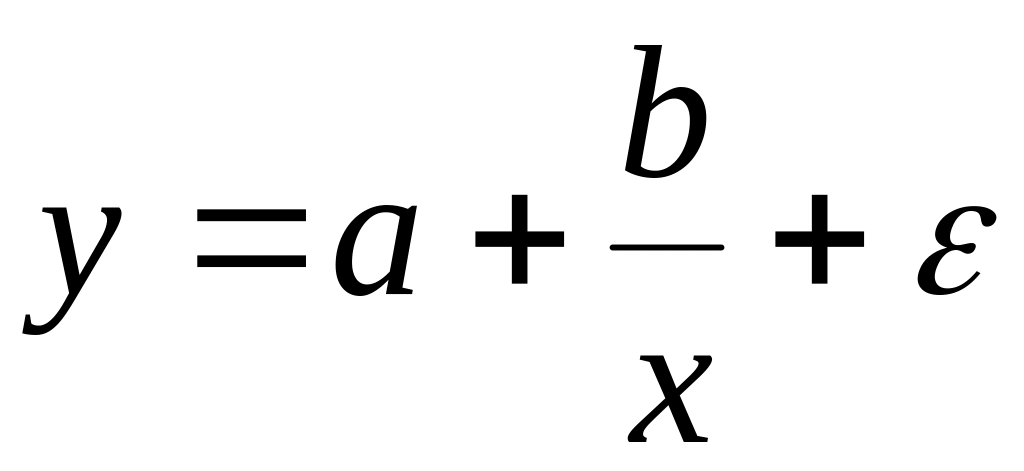
Регрессии, нелинейные по оцениваемым параметрам:

• степенная ;

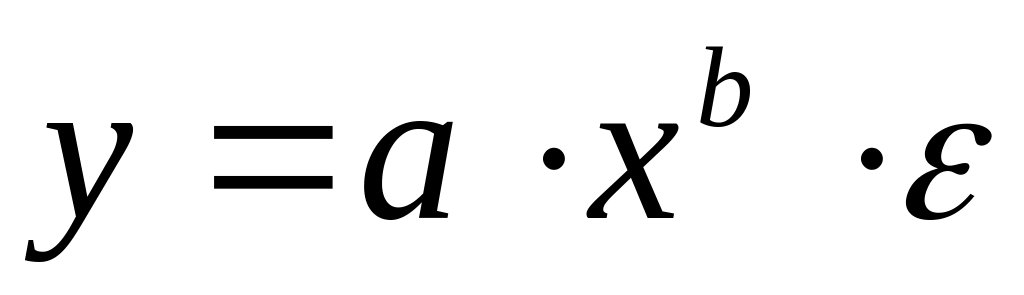• показательная ;

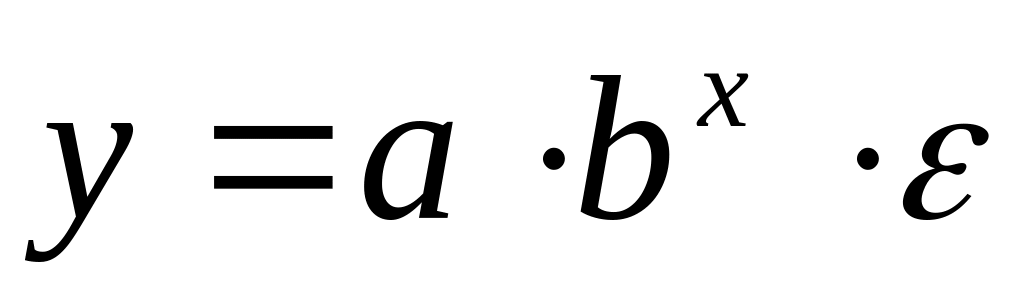• экспоненциальная .

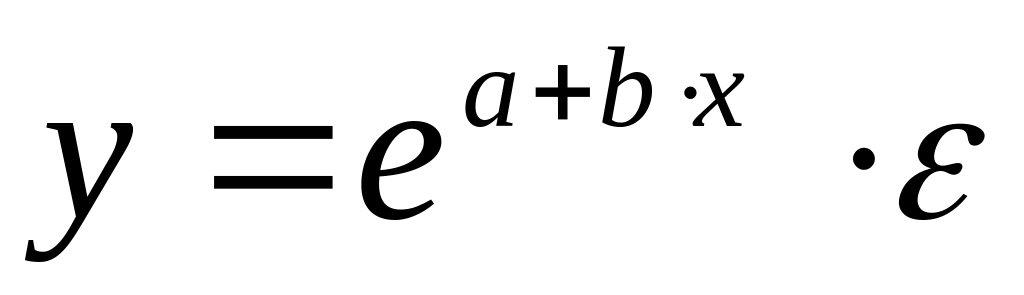Построение уравнения регрессии сводится к оценке ее параметров. Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений от значений была минимальной. Он получил название метод наименьших квадратов (МНК). По данному методу параметры вычисляются:

Для анализа силы линейной зависимости вычисляется коэффициент парной корреляции для линейной регрессии ( ):

и индекс корреляции для нелинейной регрессии :

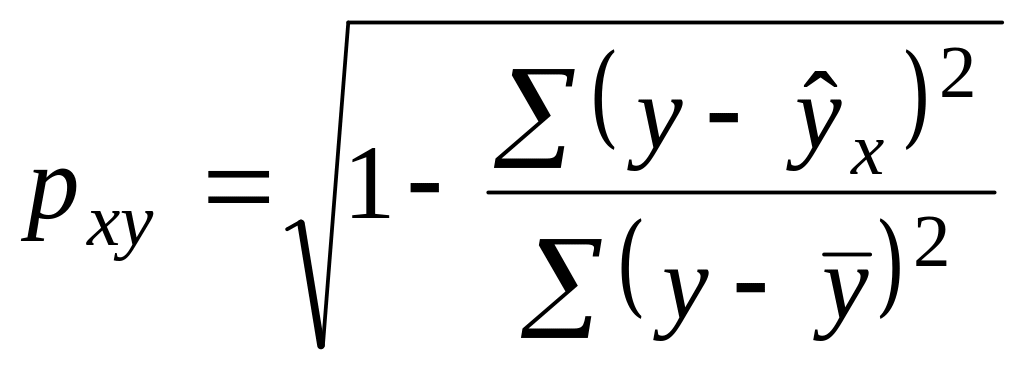
Для оценки качества построенной модели используется коэффициент детерминации, а также средняя ошибка аппроксимации.

Коэффициент детерминации - одна из наиболее эффективных оценок адекватности регрессионной модели, мера качества уравнения регрессии; характеристика прогностической силы анализируемой регрессионной модели. Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных; чем ближе он к единице, тем лучше регрессия описывает зависимость между объясняющими и зависимыми переменными. В случае парной регрессии он будет совпадать с квадратом коэффициента корреляции:

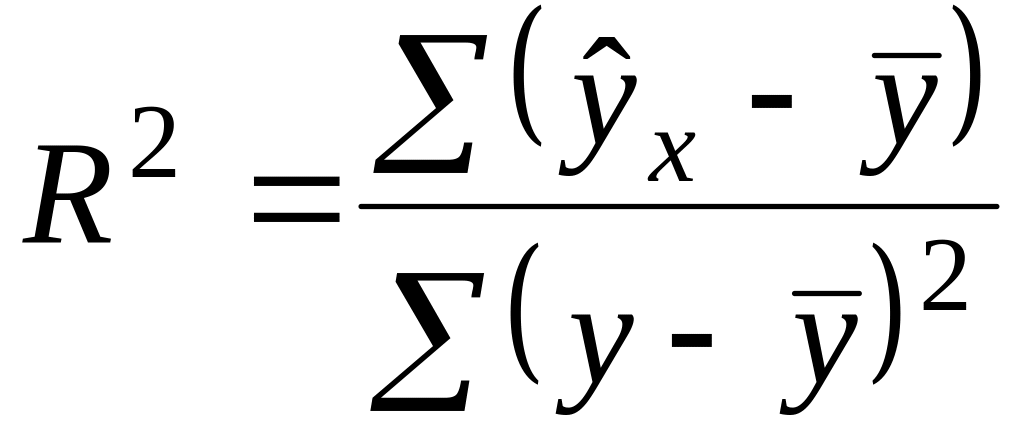
Средняя ошибка аппроксимации, т.е. среднее отклонение расчетных значений от фактических, определяется по формуле:

.

Средний коэффициент эластичности показывает, на сколько процентов по совокупности результат у изменится от своей средней величины при изменении фактора х на 1% от своего среднего значения:

F-тест – оценивание качества уравнения регрессии- состоит в проверке гипотезы о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического и критического(табличного) значений F-критерия Фишера. определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

,

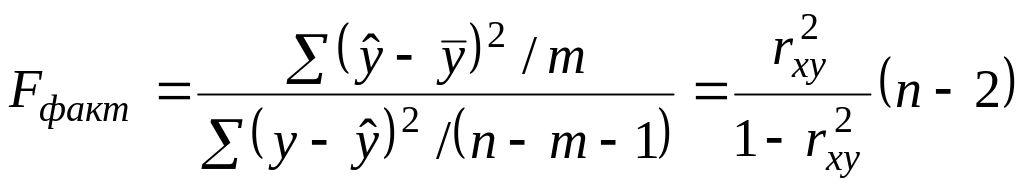где n – число единиц совокупности;

m – число параметров при переменных х.

Если < , то - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если > , то гипотеза не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза о случайной природе показателей, т. е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

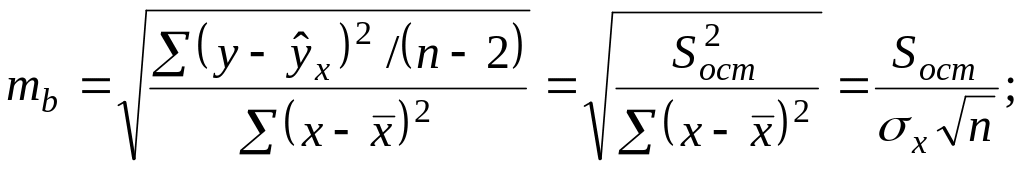
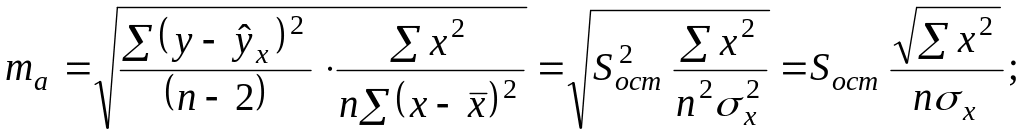
Если < , то отклоняется, т. е. и не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если , то гипотеза не отклоняется и признается случайная природа формирования a, b или .

Для расчета доверительного интервала определяем предельную ошибку для каждого показателя:

Формулы для расчета доверительных интервалов имеют следующий вид:

Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего(прогнозного) значения . Вычисляется средняя ошибка прогноза:

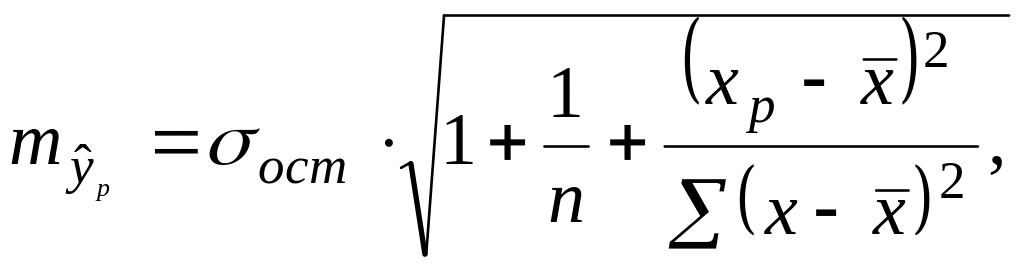
где

и строится доверительный интервал прогноза:

где .

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Пример

По территориям Восточно-Сибирского и Дальневосточного районов известны данные

Район	Потребительские расходы на душу населения, тыс. руб., y	Денежные доходы на душу населения, тыс. руб., x
1	408	524
2	249	371
3	253	453
4	580	1006
5	651	997
6	139	217
7	322	486
8	899	1989
9	330	595
10	446	1550
11	642	937
12	542	761
13	504	767
14	861	1720
15	707	1735
16	551	1052

Требуется:

1. Построить поле корреляции и сформулировать гипотезу о форме связи.

2. Рассчитать параметры уравнений обратной и гиперболической парной регрессии.

3. Оценить тесноту связи с помощью показателей корреляции и детерминации.

4. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оценить с помощью средней ошибки аппроксимации качество уравнений.

6. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.

7. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости =0,05.

Решение:

Гиперболическая функция имеет вид: y=a+b/x. Введем замену, чтобы перейти к линейной функции X=1/x. Воспользуемся встроенной функцией ЛИНЕЙН в (EXCEL) для вычисления коэффициентов регрессионного уравнения (a,b, R^2), где массив1: это исходные значения (y), массив2: новые значения (X). Полученная гиперболическая функция: y=764,9535+(-172195)/x. Найденные значения (см. приложение 1).

-172195

764,9535

Тесноту связи между фактором x и результатом y оценим с помощью показателей корреляции и детерминации.

r(корр)=

-0,83083

- воспользовались встроенной функцией КОРРЕЛ, где массив1: это исходные значения (y), массив2: новые значения (X). Он показывает, что связь умеренная и обратная.

Индекс детерминации, найденный с помощью функции ЛИНЕЙН и равный 0,690277 показывает, что вариация результата на 69% объясняется вариацией фактора х.

Средняя ошибка аппроксимации, т.е. среднее отклонение расчетных значений от фактических, определяется по формуле: =(1/n)*(y-y^)/y*100%.

А(сред. Ошиб. Аппрокс.)=

25,5307

Она равна 25,5%.

Средний коэффициент эластичности рассчитывается по формуле:

Э=x(x_сред./y_сред.). Он показывает, что в среднем по совокупности результат у изменится на 0,31% от своей средней величины при изменении фактора х на 1% от своего среднего значения.

Э(сред.коэфф. Эластичности)=

0,311609

F-тест - оценивание качества уравнения регрессии – состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравним фактическое и табличное значение F-критерия Фишера.F(факт.)>(табл.), т.е. 31,2>4,6.Гипотеза Н₀ отклоняется и признается статистическая значимость и надежность уравнения регрессии (Приложение2).

Прогнозное значение у_р определяется путем подстановки в уравнение регрессии Y^=a+b*x, где x – соответствующее прогнозное значение x_p=1,05*x_{среднее}. Вычисляем среднюю стандартную ошибку прогноза m(y(прог.)) – (см.приложение 2) и строим доверительный интервал - (см.приложение 2).

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей по формулам:

t_b=b/m_b, t_a=a/m_a, t_r=r/m_r

Случайные ошибки параметров регрессии и коэффициента корреляции определяются по формулам:

, ,

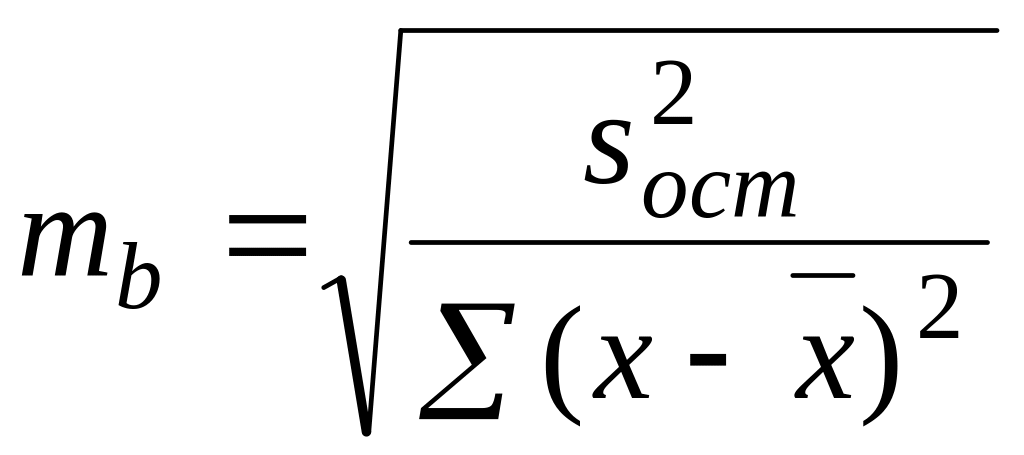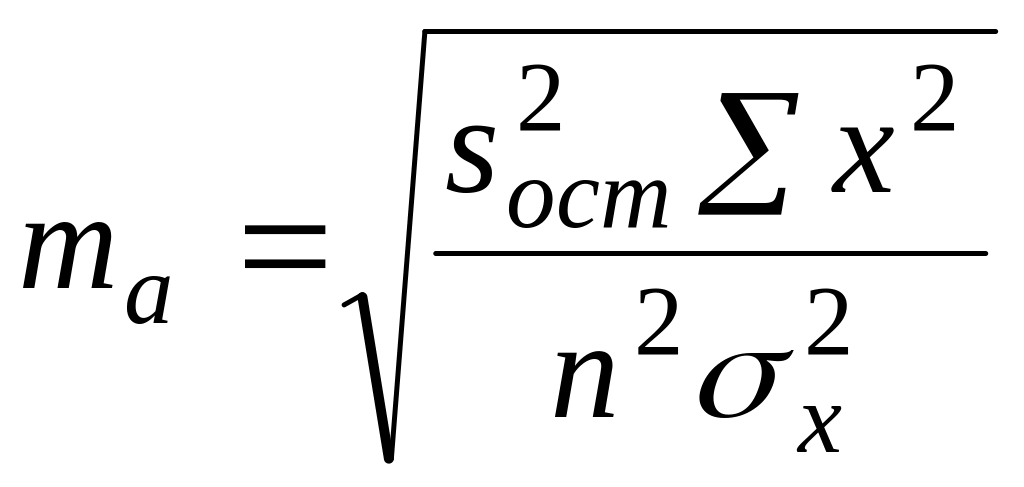Выдвигаем гипотезу Н₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля.

Сравнивая фактическое и критическое (табличное) значения t-статистики – принимаем или отвергаем гипотезу Н₀. Если t-табл.>t-факт., то гипотеза не отклоняется и признается случайная природа формирования а, b, r. (см. приложение 3). Видно, что t-табл. во всех случаях (а, b, r) больше, чем t-факт., поэтому гипотеза не отклоняется.

Для расчета доверительного интервала определяем предельную ошибку  для каждого показателя:

ПРИЛОЖЕНИЯ:

	x	y	X=1/x	X*y	X^2	Y^	y-Y^	(y-Y^)^2	y-yср	(y-yср)^2
	524	408	0,001908	0,778626	3,64198E-06	436,3374	-28,33737885	803,007	-97,625	9530,641
	371	249	0,002695	0,671159	7,26528E-06	300,8165	-51,81645591	2684,945	-256,625	65856,39
	453	253	0,002208	0,558499	4,87308E-06	384,8324	-131,8324281	17379,79	-252,625	63819,39
	1006	580	0,000994	0,576541	9,88107E-07	593,7856	-13,78564665	190,0441	74,375	5531,641
	997	651	0,001003	0,652959	1,00603E-06	592,2405	58,75949922	3452,679	145,375	21133,89
	217	139	0,004608	0,640553	2,12364E-05	-28,5711	167,5711046	28080,08	-366,625	134413,9
	486	322	0,002058	0,662551	4,23377E-06	410,6431	-88,64311634	7857,602	-183,625	33718,14
	1989	899	0,000503	0,451986	2,52773E-07	678,3799	220,6200983	48673,23	393,375	154743,9
	595	330	0,001681	0,554622	2,82466E-06	475,5504	-145,5503918	21184,92	-175,625	30844,14
	1550	446	0,000645	0,287742	4,16233E-07	653,86	-207,8600322	43205,79	-59,625	3555,141
	937	642	0,001067	0,685165	1,13899E-06	581,181	60,81902786	3698,954	136,375	18598,14
	761	542	0,001314	0,712221	1,72675E-06	538,6791	3,320946605	11,02869	36,375	1323,141
	767	504	0,001304	0,657106	1,69984E-06	540,4491	-36,44912708	1328,539	-1,625	2,640625
	1720	861	0,000581	0,500581	3,38021E-07	664,8402	196,1598022	38478,67	355,375	126291,4
	1735	707	0,000576	0,407493	3,32201E-07	665,7057	41,29426952	1705,217	201,375	40551,89
	1052	557	0,000951	0,529468	9,03584E-07	601,2702	-44,27017138	1959,848	51,375	2639,391
Сумма	15160	8090	0,024096	9,327271	5,28777E-05	8090	-2,27374E-13	220694,3	0	712553,8
среднее	947,5	505,625	0,001506	0,582954	3,30486E-06	505,625	-1,42109E-14	13793,4	0	44534,61