6.3. Изотермы реальных газов.

Обозначим .

Умножив уравнение (2) на , получаем

(3)

Все реальные газы с уменьшением плотности приближаются по своим свойствам к идеальным газам, поэтому уравнение Ван-дер-Ваальса при переходит в уравнение Менделеева - Клапейрона.

Раскрыв скобки в уравнении (3) и умножив на , получаем

(4)

Мы получили кубическое уравнение относительно , коэффициенты которого зависят от параметров .

В зависимости от соотношения между коэффициентами решения уравнения могут быть либо все три вещественными, либо одно вещественное и два комплексных, не имеющих физического смысла.

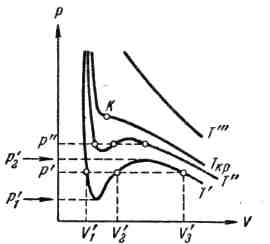На рис.6.5 изображены изотермы Ван-дер-Ваальса для нескольких значений температуры.

При температуре и давлении в пределах от до коэффициенты в (4) таковы, что все три решения вещественные; при других коэффициентах уравнение имеет только одно вещественное решение.

Различие между тремя вещественными решениями с ростом температуры уменьшается (ср. изотермы и , > ).

Начиная с определенной, своей для каждого вещества температуры вещественным остается только одно решение уравнения (4). Температура , называемая критической.

Если повышать температуру, то точки, соответствующие решениям уравнения , , все больше сближаются, сливаясь при критической температуре в одну точку (на рис. Точка К).

Точка К называется критической. Ей соответствуют три совпадающих вещественных решения уравнения (4). Касательная к критической изотерме в точке К является пределом, к которым стремятся секущие и и т.д. при приближении температуры к критической. Следовательно, эта касательная , ак и все секущие , параллельна оси V, так , что производная в точке К. Кроме того в точке перегиба должна быть равна нулю и вторая производная

Из уравнения (1) выразим давление:

Продифференцируем это уравнение по :

В критической точке при эти выражения должны обращаться в ноль:

Для критической точки

Мы получили систему из трех уравнений с неизвестными .

Решение этой системы имеет вид

Таким образом, зная константы Ван-дер-Ваальса и , можно найти соответствующие критической точке , которые называются критическими величинами. И , наоборот, по известным критическим величинам могут быть найдены значения констант Ван-де- Ваальса.

Для критических величин , в то время как

согласно уравнению Менделеева - Клапейрона для идеального газа .

6.4. Внутренняя энергия реального газа.

Взаимодействие между молекулами реального газа обуславливает их взаимную потенциальную энергию , которая переходит во внутреннюю энергию газа наряду с кинетической энергией движения молекул .

Найдем энергию ван-дер-ваальсовского газа.

Внутренняя энергия такого газа , где

— суммарная кинетическая энергия молекул в Ц-системе (связанной с сосудом),

— суммарная энергия взаимодействий молекул (собственная потенциальная энергия).

Найдем . : Работа сил притяжения равна убыли внутренней энергии .

Силы притяжения характеризуются внутренним давлением в уравнении Ван-дер-Ваальса.

Тогда элементарная работа этих сил , где знак минус обусловлен тем, что при расширении газа ( >0) работа должна быть отрицательной, < 0.

Итак, .

Мы представили как убыль некоторой величины — она и является энергией = .

При .

Суммарная же кинетическая энергия зависит от поступательного и внутреннего движений молекул, и определяется как .

Таким образом, внутренняя энергия моля ван-дер-ваальсовского газа

где .

Если газ расширяется в пустоту без теплообмена с окружающими телами, то А = U, Q = 0, и согласно первому началу в этом процессе U= сопst. Значит, с ростом объема температура газа уменьшается (в отличие от идеального газа).

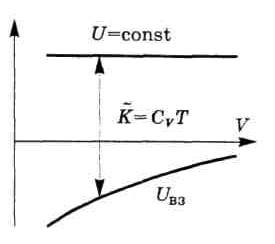Это можно представить и наглядно (рис. 6.6).

Видно, что при расширении газа (увеличении объема V) в случае U=const суммарная кинетическая энергия молекул газа, а значит и температура T, уменьшается. Газ охлаждается.

Теперь получим то же выражение для внутренней энергии, исходя из того, что внутренняя энергия является термодинамическим потенциалом

Из уравнения состояния ван-дер-ваальсовского газа следует, что .

Отсюда .

Подставив это выражение, получим .

Произведя интегрирование по V, найдем, что .

Вид функции f (Т) можно установить, воспользовавшись тем, при выражение для внутренней энергии ван-дер-ваальсовского газа должно переходить в выражение для внутренней энергии идеального газа

U = T.

В итоге мы приходим к выражению которое было получено, исходя из других соображений .

Получим для моля ван-дер-ваальсовского газа этого газа уравнение адиабаты в переменных T, V, если известна его молярная теплоемкость .

Согласно первому началу термодинамики

.

Отсюда

Интегрируя это уравнение, получаем ,

Или .

Таким образом, уравнение адиабаты имеет вид .

Определим для ван-дер-ваальсовского газа разность теплоемкостей .

По определению теплоемкости

Учитывая, что получим . (4)

Найдем .

Для этого продифференцируем по T уравнение Ван-дер-Ваальса.

В результате получим . (5)

Подстановка (5) в (4) приводит к искомому результату: .