Фокусное расстояние и оптическая сила тонкой линзы.

Пусть светящаяся точка лежит на главной оптической оси, бесконечно далеко от линзы

.

В этом случае лучи от источника падают на линзу параллельно главной оптической оси. Изображение светящейся точки находится на расстоянии от линзы

.

Аналогично, если источник находится справа от линзы:

,

.

Точка, в которой пересекаются после преломления линзой лучи, падающие на нее параллельно главной оптической оси, называется главным фокусом линзы.

Расстояние от линзы до главного фокуса называется фокусным расстоянием тонкой линзы.

Видно, что

.

Фокусные расстояния равны по величине и противоположны по знаку. Это означает, что фокусы лежат по разные стороны от линзы.

Фокусное расстояние линзы равно

.

В зависимости от - величины могут быть как положительными (действительными), так и отрицательными (мнимыми).

Если фокусы действительны (положительны), то это означает, что параллельные лучи после преломления линзой сходятся. В этом случае линза называется собирательной или положительной.

При мнимых (отрицательных) фокусах параллельные лучи после преломления в линзе становятся расходящимися. Такие линзы называются рассеивающими или отрицательными.

Если , то собирательные линзы: двояковыпуклые, плосковыпуклые, вогнуто – выпуклые.

Рассеивающие линзы – двояковогнутые, плоско-вогнутые, выпукло-вогнутые.

Плоскость, проведенная через главный фокус линзы, перпендикулярно к главной оптической оси, называется фокальной плоскостью линзы.

Если на линзу падает пучок лучей, параллельный побочной оптической оси, то после преломления собирательной линзой, лучи сходятся в точке , являющейся

,

.

Если перейти к обозначениям , то

,

,

.

Для собирательной линзы оптическая сила положительна, для рассеивающей – отрицательна.

Построение изображений в тонкой линзе.

Для построения изображений необходимо указать расположение линзы и ее главных фокусов.

.

При использовании формулы тонкой линзы используют следующие правила расстановки знаков:

1. если линза собирающая, то перед ставится знак плюс; если линза рассеивающая, то перед ставится знак минус.

2. перед ставится плюс, если изображение действительное и минус, если изображение мнимое.

3. если неизвестны, то перед , ставится знак плюс. Если в результате вычислений получаются отрицательные значения, это означает, что фокус или изображение являются мнимыми.

4. мнимым источником называется точка, в которой сходятся воображаемые продолжения лучей, падающих на линзу. Для мнимого источника перед нужно взять знак минус.

Для построения изображений, получаемых с помощью тонкой линзы обычно используют следующие «удобные лучи»

1. Луч, проходящий через оптический центр линзы не преломляясь

2. Луч, параллельный главной оптической оси, после преломления в линзе, проходит через фокус.

3. Луч, проходящий через фокус, после преломления идет параллельно главной оптической оси.

Построим изображения светящегося предмета в собирающей линзе.

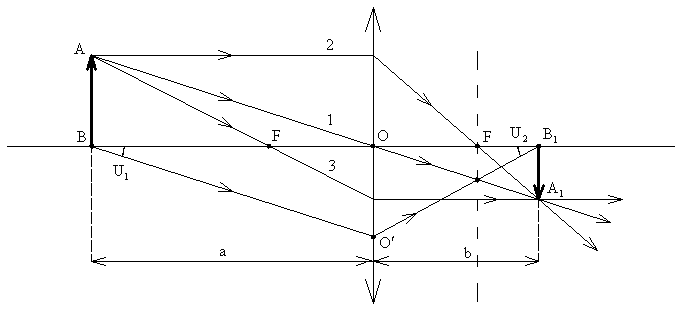
Лучи 1,2,3 позволяют найти точку - изображение точки . Из светящейся точки проведем луч, параллельный побочной оптической оси . После преломления в линзе луч пересекается с лучом в некоторой точке фокальной плоскости, проведенный через фокус. Продолжая луч до пресечения с главной оптической осью, получим точку , являющуюся изображением .

Увеличение, даваемое линзой, равно

.

Из треугольников и запишем

,

.

Обозначим - углы, образованные лучами и с главной оптической осью.

Угловым увеличением называется величина

.

Для параксиальных лучей запишем

,

.

Из , следует, что

.