27. Колебания системы с одной степенью свободы. Резонанс в системе с линейным демпфированием.

Гармонический осциллятор

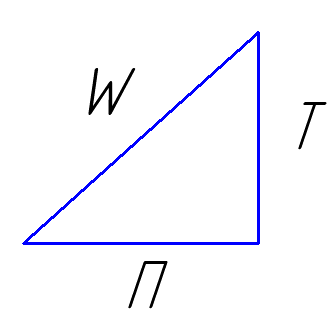
до φ=30⁰ sinφ≈φ

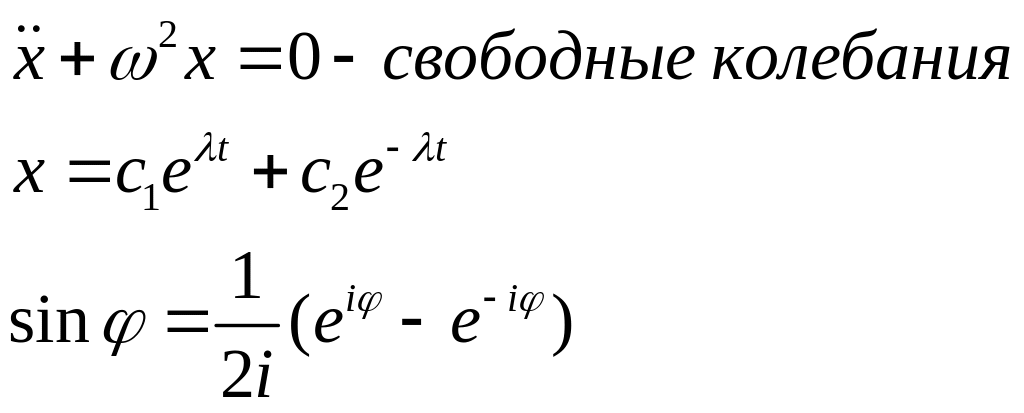
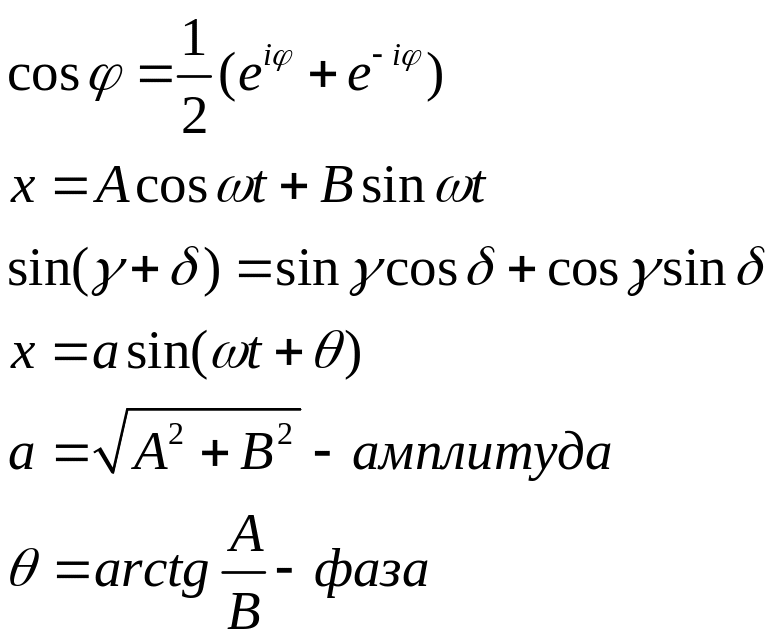
Демпфер

Резонанс- особое состояние колебаний системы, находящейся под действием гармонической вынуждающей силы, при которой частота вынуждающей силы равна частоте собственных колебаний.

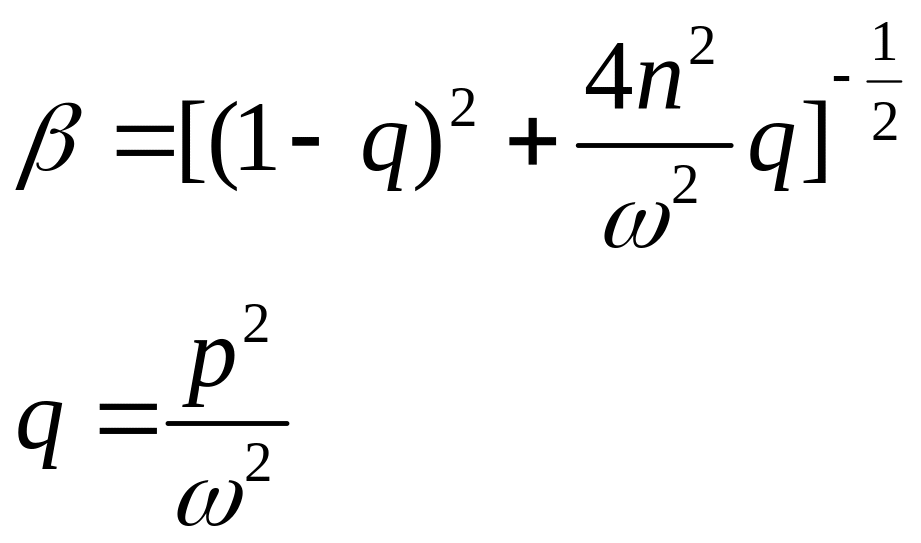
В случае системы с трением амплитуда при резонансе ограничена. Максимум амплитуды расположен на АЧХ левее точки резонанса, а сдвиг фаз между f(t) и x(t) не изменяется – π/2⇒ критерием резонанса следует считать именно сдвиг фаз между f(t) и x(t).

28. Метод Бубнова-Галеркина.

Из метода Рица

, где – ортогональные функции.

если решение

3 Этапа решения:

1) Аппроксимация форм колебания

2) Переход к системе СОДУ

3) Решение СОДУ

Пункт №1:

(1)

(2) – удовлетворяет Гр.У. и Н.У.

(1) – упрощается (отбрасываем трение и правую часть)

(3)

(4)

(4) → (3)

(5)

– неизвестная форма;

(6), где – неизвестная константа.

– ортогональные функции, удовлетворяющие всем Гр.У.

(6) → (5)

(7)

Домножаем на и интегрируем :

(8)

(8) представляет собой САУ.

(10)

Пункт №2: Переход к СОДУ

(10) → (2)

(11)

(11) → (1)

(12)

Домножаем на и интегрируем :

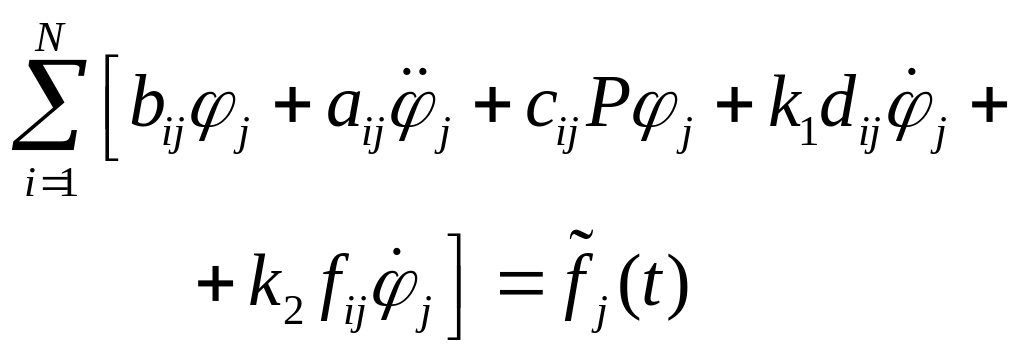(13)

Пункт №3: Решение СОДУ (13) с заданными начальными данными.

Алгоритм метода Бубнова-Голеркина:

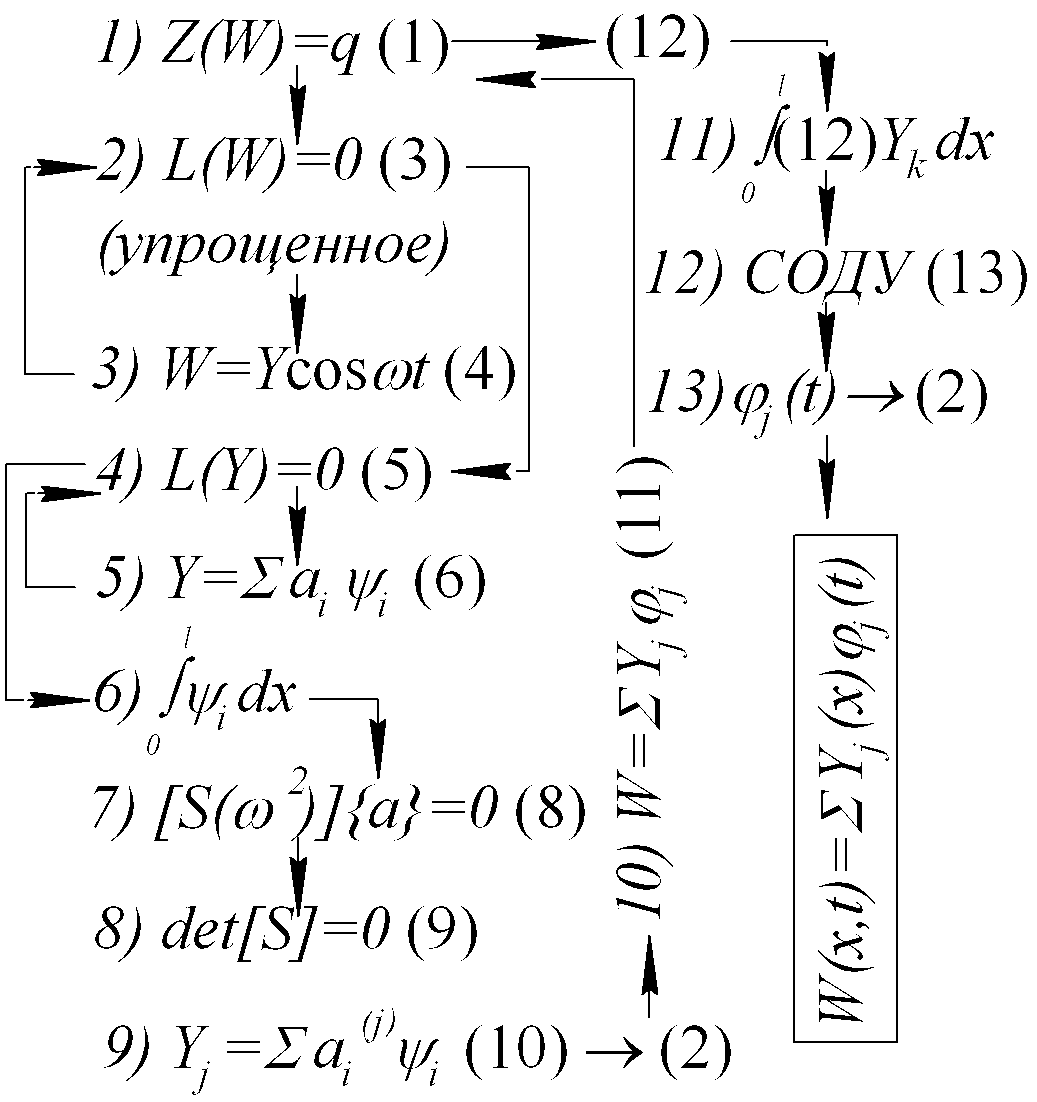
29. Метод нормальных колебаний. Условия ортогональности. Решение ищем в виде:

Уравнение нормальных колебаний (УНК):

(1)

(2)

1. Подставляем в (2)

(3)

- решение уравнения нормальных колебаний (удовлетворяет всем граничным условиям).

Если EI=const, =const, то - балочная функция.

С_i – находят из граничных условий.

Условия ортогональности:

Если :

1. Решение уравнения нормальных колебаний.

2. Удовлетворяет граничным условиям.

То - ортогональные функции.

Пусть , - решения УНК, удовлетворяющие граничным условиям.

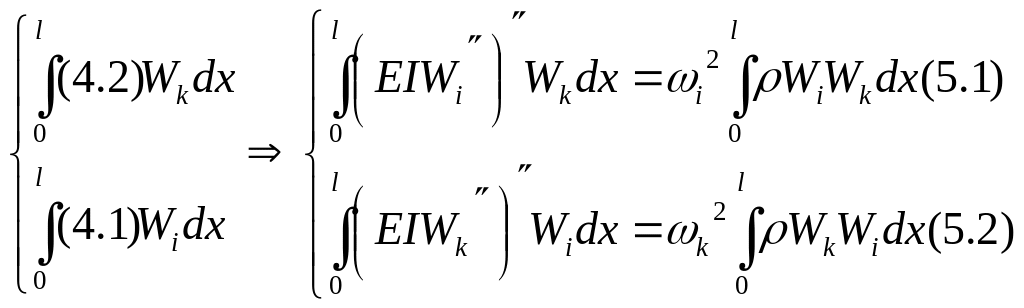Вычтем из (5.1) – (5.2):

Если i=k, то

Если i k, то

Выполняется условие ортогональности.

М-ортогональность:

К-ортогональность:

Вынужденные поперечные колебания стержня:

(1)

(2)

- приближённая функция времени

- решение уравнения УНК (удовлетворяет всем граничным условиям), i=1…N.

2. подставляем в (1):

(3)

Нормализация:

1. (3) умножим на W_j

2. проинтегрируем по dx на интервале 0-l

,

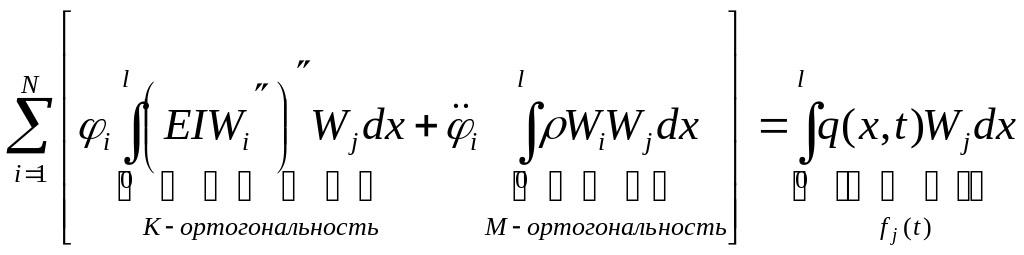
Где ,

Колебания балки с трением:

Внешнее трение:

Внутреннее демпфирование:

- модель Фойгта

Уравнение колебаний:

(1)

(2)

(2) подставляем в (1):

(3)

Нормализация:

1. (3) умножим на W_j

2. проинтегрируем по dx на интервале 0-l

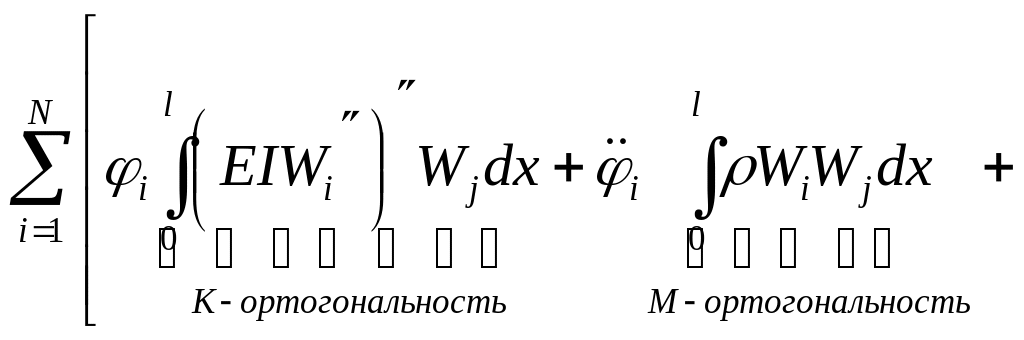
, (4)

,

Если E, I, =const

Тогда уравнение (4) примет вид:

,

30.Параметрические колебания под действием высокочастотного параметрического возбуждения. Условие динамической устойчивости перевёрнутого маятника.

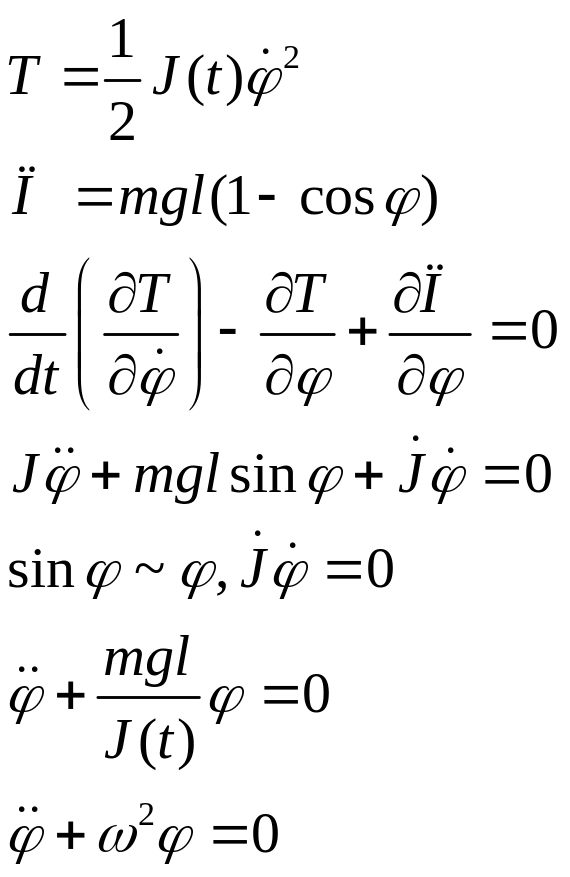
система с одной степенью свободы, свободные колебания

1. Низкочастотное параметрическое возбуждение p~ω

2. Высокочастотное параметрическое возбуждение p>>ω

Высокочастотное параметрическое возбуждение.

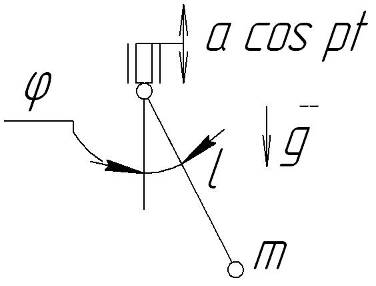
Период быстрого движения

Т_Б – осцилляция; Т_М – эволюция.

Теорема о медленном и быстром движении.

1)Быстрое движение может содержать медленное, а наоборот – нельзя!

2) - осреднение

Пример.

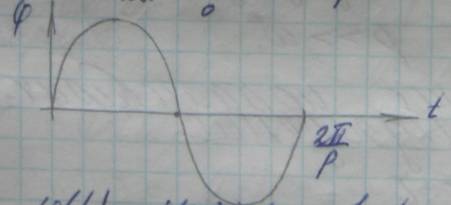
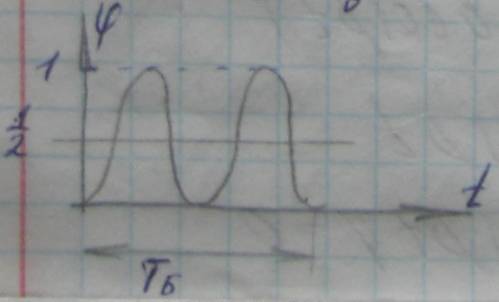
3. явно быстрое ;

4. смешанное движение ;

5. 

6. Решение в виде: Осредняем (6)

128