23.Вынужденные колебания систем с конечным числом степеней свободы. Резонанс. Динамическое демпфирование.

Если - резонанс

Если - антирезонанс

Динамическое демпфирование:

Существует интересная возможность практической борьбы с колебаниями; ею пользуются в некоторых областях техники. Допустим, что имеется некоторая система с одной степенью свободы, подподверженная действию гармонической вынуждающей силы. Усложнив систему путем добавления дополнительной массы на упругой связи и подчинив значения жесткости и массы дополнительной части условию, можно добиться устранения вибраций основной части системы; в этом случае дополнительная часть системы называется динамическим гасителем колебаний {динамическим виброгасителем).

24.Метод степенных рядов.

(1)

Тогда:

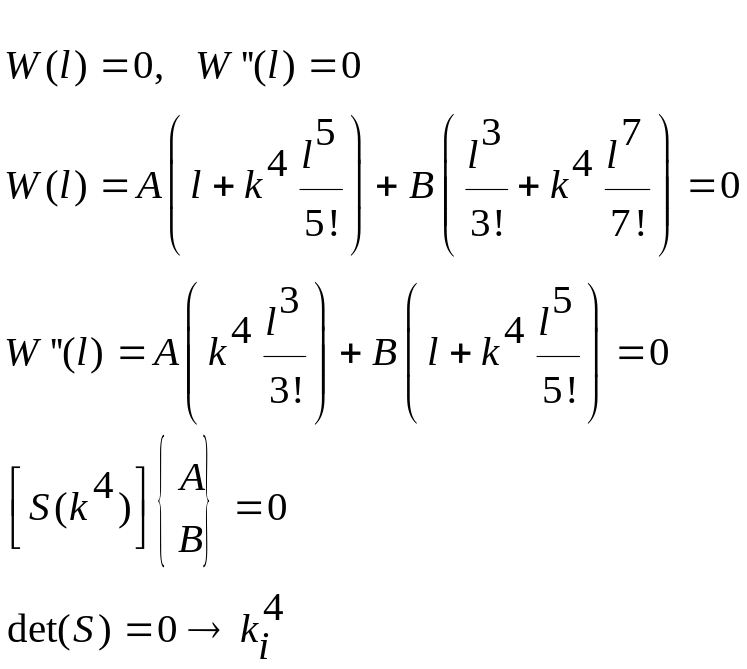
Пример: Случай разделения балки на участки.

6 уравнений, 2 гр. Условия при х=l, 4 условия стыковки при х=a

25.Колебания с линейным демпфированием в системе с конечным числом степеней свободы. Условия разделения сду при переходе к главным координатам

Модели трения:

- сухое трение

-вязкое трение

-гидродинамическое трение

Трение бывает внешним и внутренним.

Демпфер.

Система с вязким трением никогда не остановится.

Систему останавливает вязкое трение.

n- декремент (затухания) колебаний

1)

X= непериодическая (квазипериодическая) функция

-логарифмический декремент затухания

2) Апериодическое движение

Условия разделения СДУ при переходе к главным координатам:

Условие ортогональности

и все уравнения (7) складываются

Так как матрица диагонально симметрична

если

Условие М-ортогональности

Применение условия ортогональности:

Если известна

где -вектор главных нормальных координат

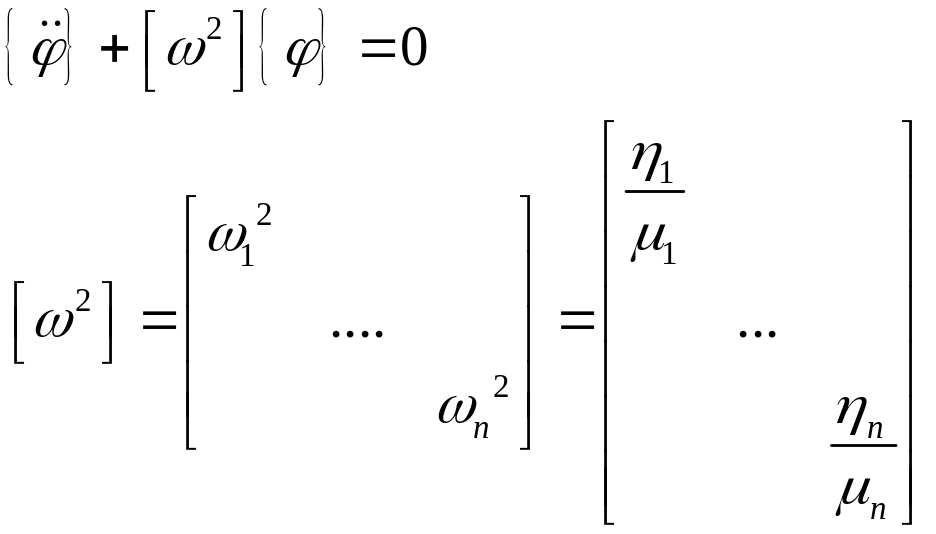
Таким образом, нормализация для систем с n степенями свободы происходит следующим образом:

26. Продольные колебания стержней поперечного сечения. Вывод уравнений, Граничные условия, Точное решение на примере консольно закрепленного стержня.

Колебания систем с распределенными параметрами.

Модели:

1) Трехмерные

2) Двумерные: пластинки и оболочки

3) Одномерные: стержни, балки, торсионы.

Материал:

1) Однородный

2) Изотропный

3)

Уравнение продольных колебаний стержня

Допущения:

1) Сечение остается плоским (неизменное сечение)

2) Деформации происходят вдоль оси ox

3) – малая величина

4) – малая величина.

, S – сила, прилож-я к сечению.

, где а – скорость звука.

Н.У.:

Граничные условия

Гр.У.:

Кинематические и силовые условия зависят от вида закрепления на левом ( ) или на правом ( ) крае:

1) Заделка:

2) Свободный край:

3) Упругое закрепление:

Виды решения:

– колебания;

– волна.

Точное решение на примере консольно закрепленного стержня.

(1), где точка означает производную по времени, а штрих – производную по координате.

Н.У.:

Гр.У.:

Решение ищем в виде:

(2) – колебания;

– форма колебаний.

– обобщенная координата.

(2) → (1):

(3)

Необходимо решить 2 задачи:

1) Краевая задача:

Гр.У.:

2) Задача Коши:

Н.У.:

1) Решение краевой задачи

=> Упругая система имеет бесконечное число степеней свободы.

2) Решение задачи Коши

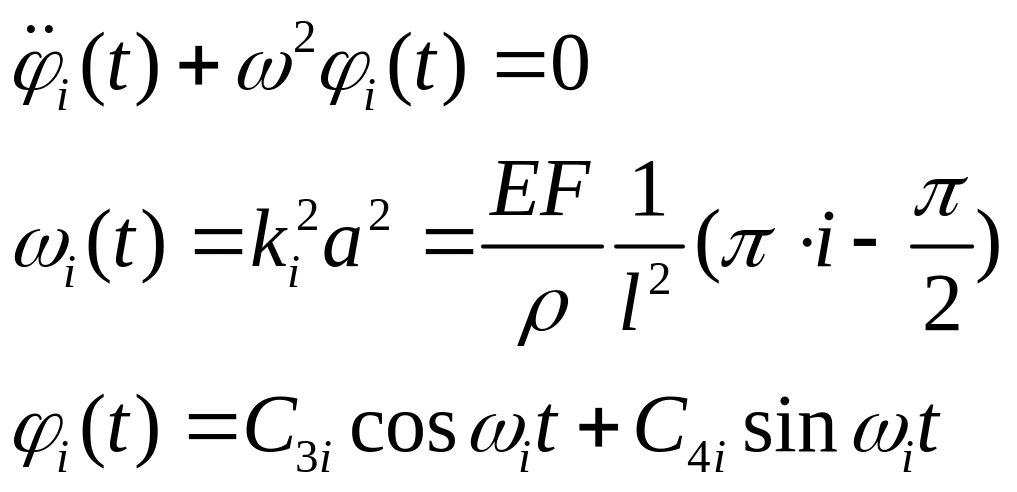
3)

– опорный коэффициент.

Н.У.:

Рассмотрим интеграл:

1) :

2) :