
- •Оглавление
- •1. Методы составления дифференциальных уравнений движения колебательных систем. Метод Лагранжа.
- •Метод Лагранжа.
- •2. Параметрические колебания с учетом малых нелинейностей. Уравнение параметрона.
- •3.Метод д’Аламбера. Энергетический метод.
- •4 Определение методом Боголюбова в первом приближении законов изменения амплитуд и фаз решения уравнения Матье.
- •7. Вынужденные колебания одной степенью свободы при отсутствии резонанса. Способы определения частных решений.
- •8. Уравнение Матье с демпфированием. Определение границ области неустойчивости в первом приближении. Условие существования резонанса.
- •9. Резонанс без демпфирования в системе с одной степенью свободы. Биения.
- •10.Второй параметрический резонанс в уравнении Матье. Границы области неустойчивости, решение и с.Д.У. Для амплитуды и фазы решения во втором приближении.
- •11. Собственные частоты и формы колебаний системы с двумя степенями свободы. Главные координаты.
- •Переход к главным нормальным координатам.
- •12. Основной параметрический резонанс в уравнении Матье. Границы области неустойчивости, решение и с.Д.У. Для амплитуды и фазы решения в первом приближении.
- •23.Вынужденные колебания систем с конечным числом степеней свободы. Резонанс. Динамическое демпфирование.
- •24.Метод степенных рядов.
- •25.Колебания с линейным демпфированием в системе с конечным числом степеней свободы. Условия разделения сду при переходе к главным координатам
- •27. Колебания системы с одной степенью свободы. Резонанс в системе с линейным демпфированием.
- •28. Метод Бубнова-Галеркина.
- •29. Метод нормальных колебаний. Условия ортогональности. Решение ищем в виде:
- •30.Параметрические колебания под действием высокочастотного параметрического возбуждения. Условие динамической устойчивости перевёрнутого маятника.
7. Вынужденные колебания одной степенью свободы при отсутствии резонанса. Способы определения частных решений.
Вынужденные колебания без трения:

Интеграл Дюамеля:
![]() - общего вида
- общего вида
![]()
![]()
Пусть
![]()
Тогда:
![]()
![]()
![]()

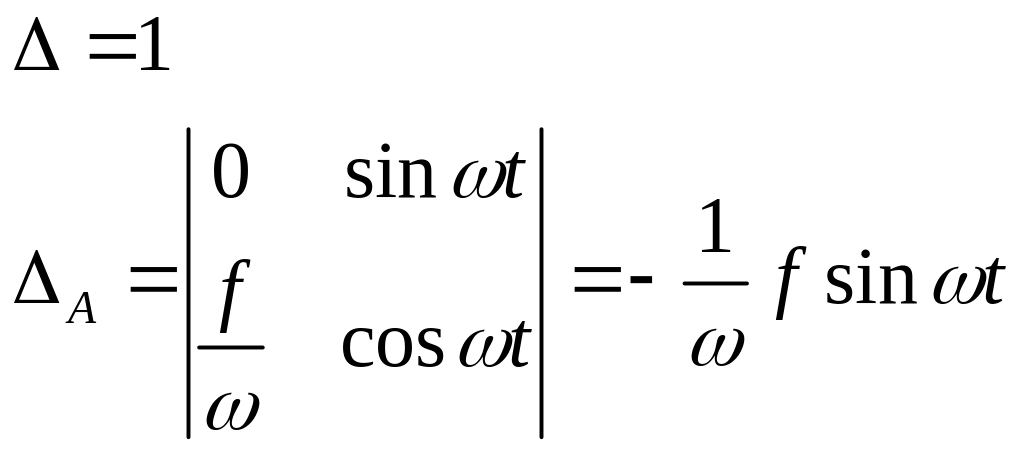
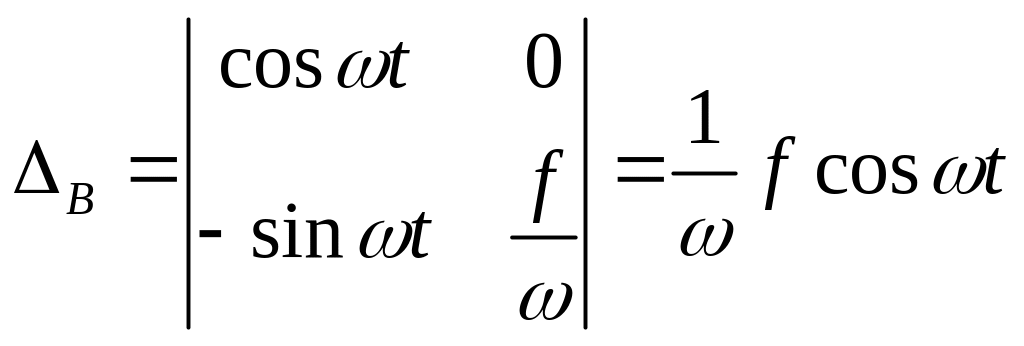


![]()
Пр:
Действие на систему гармонической вынуждающей силы.

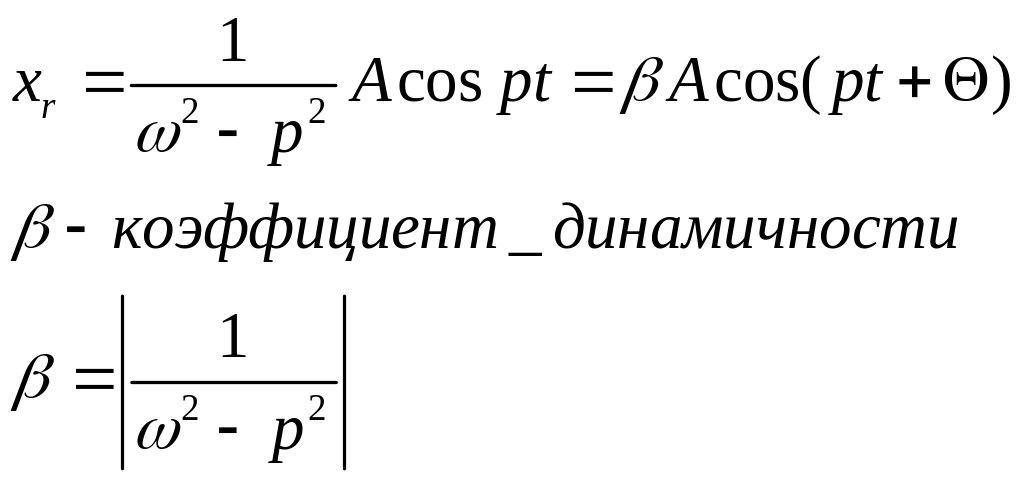

![]() разность
фаз между вынуждающей силой и откликом
системы.
разность
фаз между вынуждающей силой и откликом
системы.
![]()
![]()
f(t)=f(t+T)


Вынужденные колебания c трением:

![]()

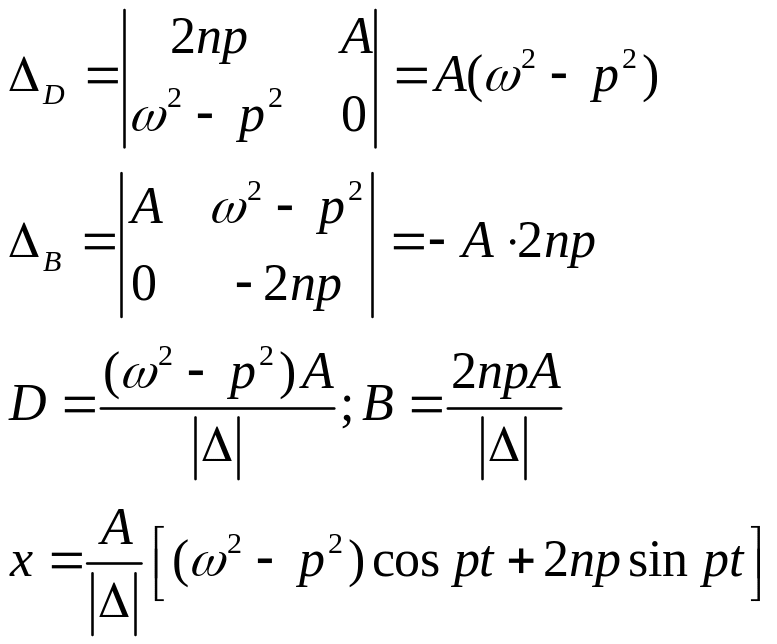

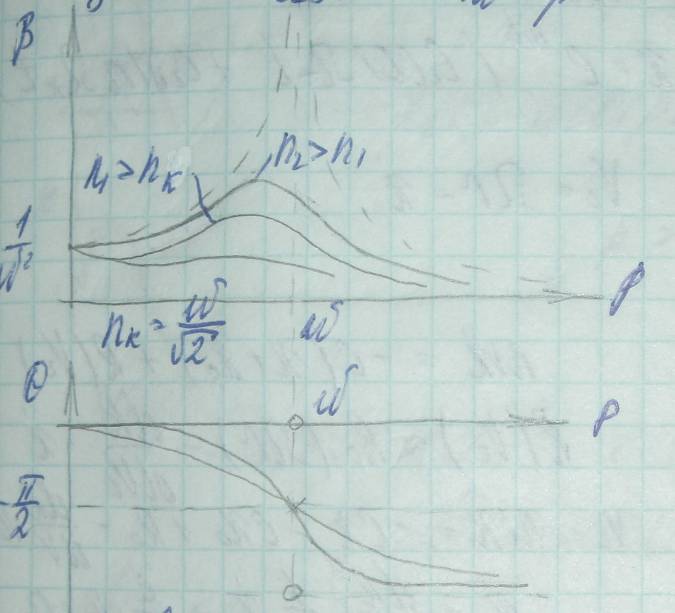

В случае системы с трением, амплитуда
при резонансе ограничена. Мах амплитуда
расположена на АЧХ левее точки резонанса,
а сдвиг фаз – между f(t)
и x(t) не
изменяется
![]() =>
критерием резонанса следует считать
изменение сдвига фаз между f(t)
и x(t).
=>
критерием резонанса следует считать
изменение сдвига фаз между f(t)
и x(t).
Случай отрицательного трения:


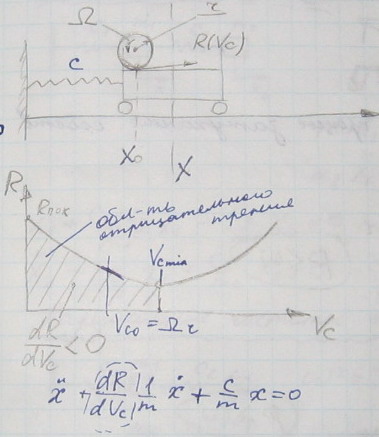
8. Уравнение Матье с демпфированием. Определение границ области неустойчивости в первом приближении. Условие существования резонанса.
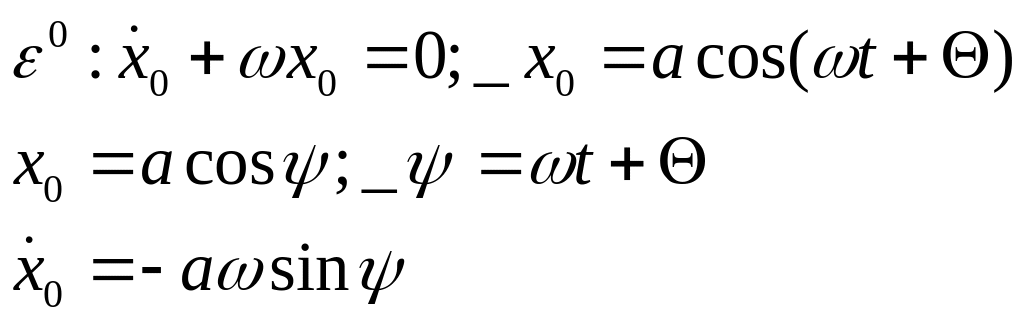

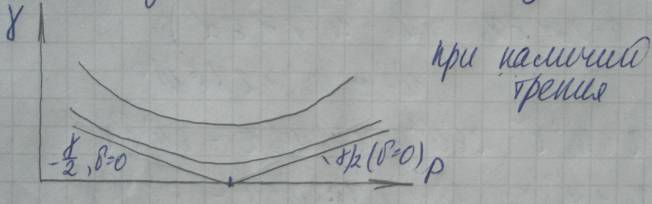
9. Резонанс без демпфирования в системе с одной степенью свободы. Биения.
-особое состояние колебательной системы,
находящейся под действием гармонической
вынуждающей силы, при которой частота
вынуждающей силы = частоте собственных
колебаний
![]()

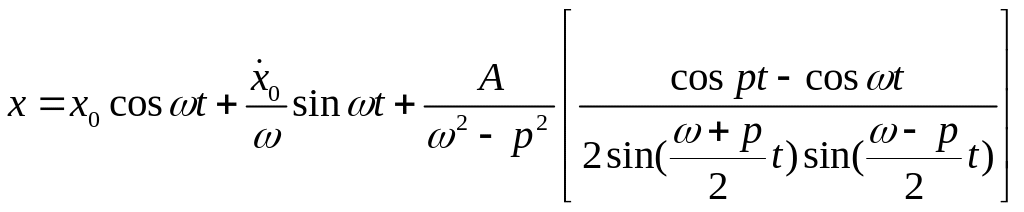

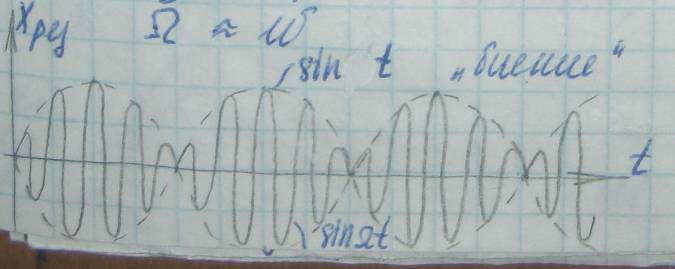
Резонанс:

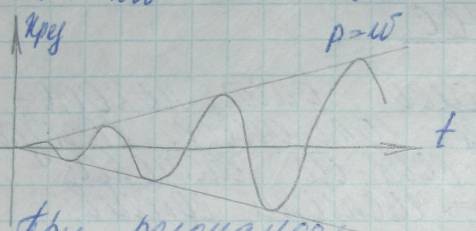
При резонансе:
рост амплитуды пропорционально t;
сдвиг по фазе между f(t) и Xрез составляет

 -
«Биение».
-
«Биение».
10.Второй параметрический резонанс в уравнении Матье. Границы области неустойчивости, решение и с.Д.У. Для амплитуды и фазы решения во втором приближении.
В некоторых случаях при периодически изменяющихся параметрах возникают нарастающие колебания системы, имеет место параметрический резонанс.
![]()
![]() -
основной параметрический резонанс.
-
основной параметрический резонанс.
![]() - резонанс второго порядка..
- резонанс второго порядка..
2-й параметрический резонанс.

![]()

![]()
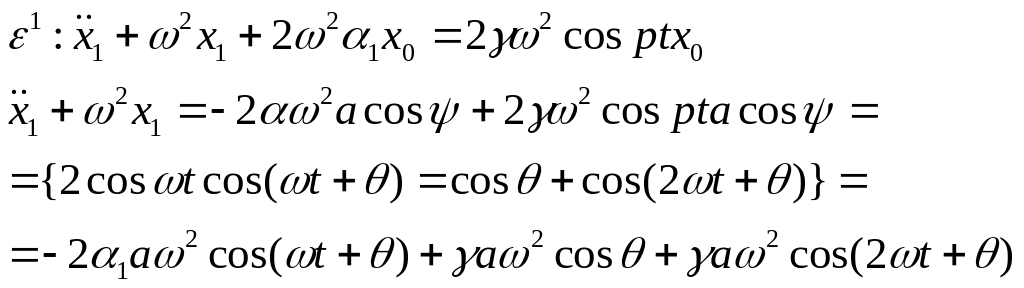
;
![]()
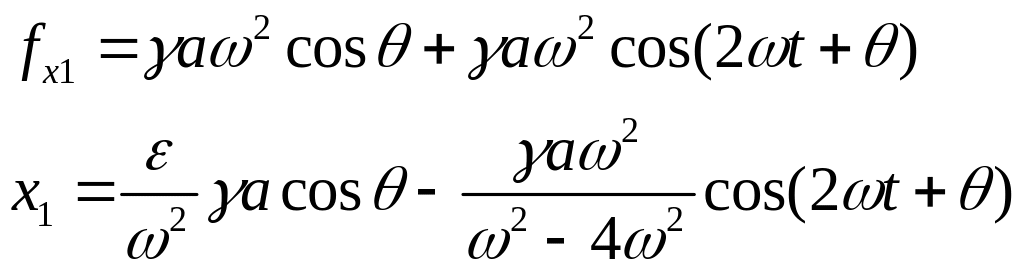
Гр. обл. неуст-ти:
![]() ;
;![]()

![]()
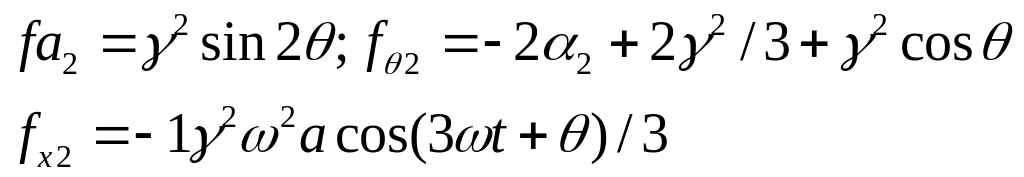

![]()
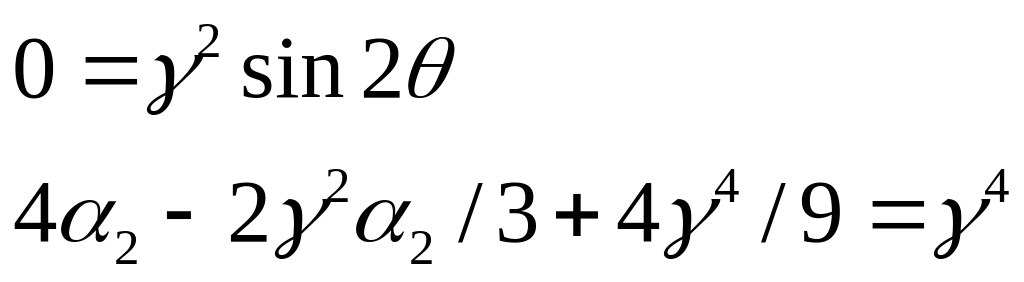
![]()
![]()
В первом приближении область неустойчивости не существует, только во втором приближении она сдвинута. т.е. трение порядка ипсилон уничтожает параметрический резонанс выше второй степени.
11. Собственные частоты и формы колебаний системы с двумя степенями свободы. Главные координаты.
Системы с 2-мя степенями свободы:
Д
 ва
тела по 1 степени свободы.
ва
тела по 1 степени свободы.
одно тело с двумя степенями свободы.
Собственные колебяния(для первого
рисунка):
![]() ;
;![]()
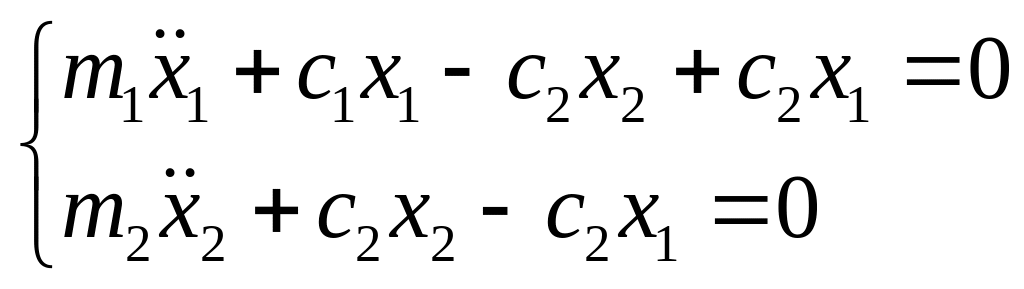 =>
=>

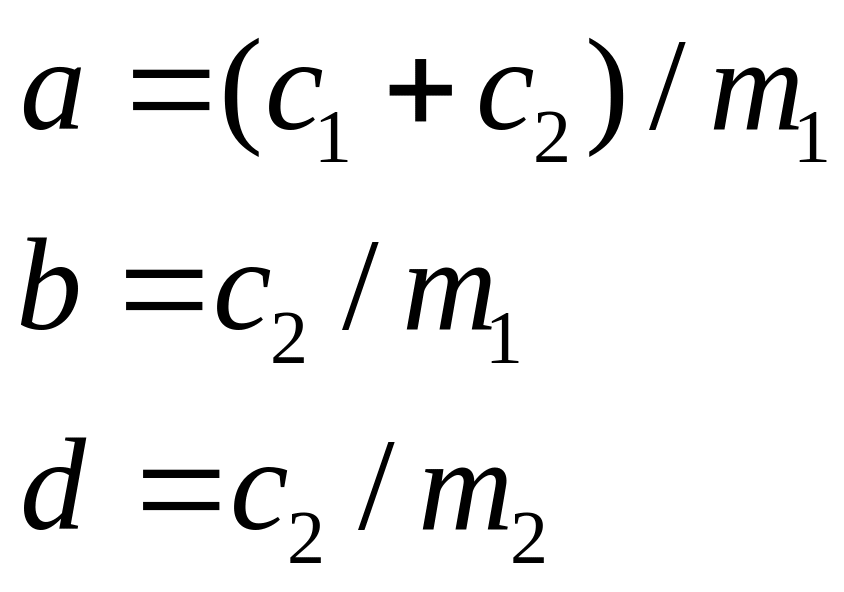
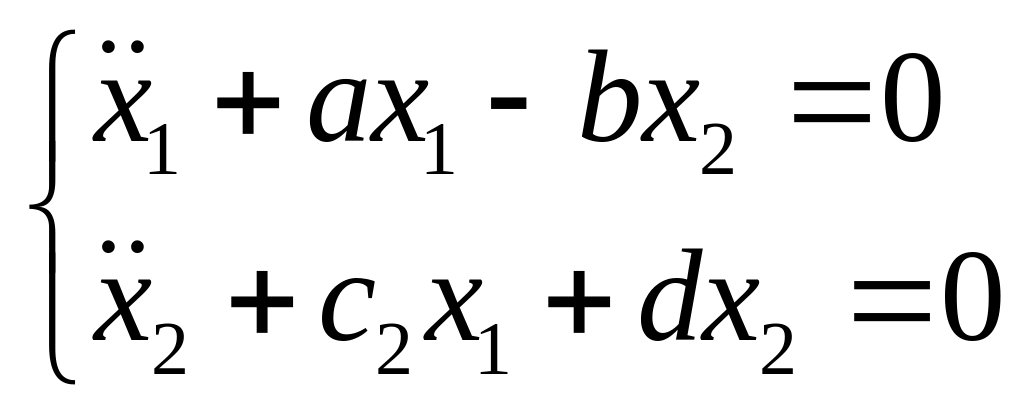
![]() -главные
колебания
-главные
колебания
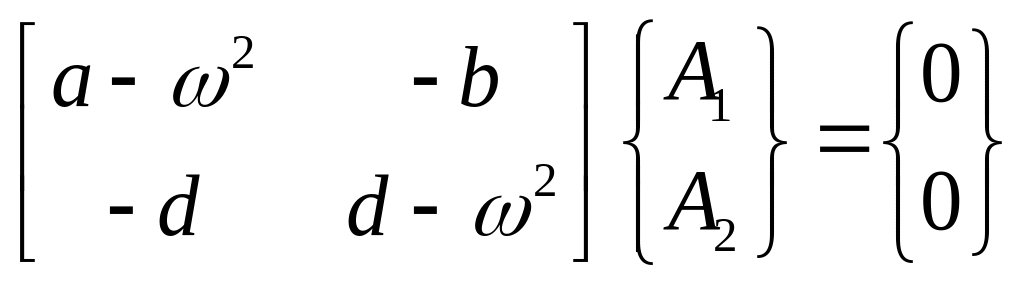 ;
;
![]()
![]()
Если положение системы, от которого
отсчитываются перемещения является
положением устойчивого равновесия, то
все корни Ур-я действительны и положительны.
Таким образом, система с 2 степенями
свободы имеет 2 частоты собственных
колебаний(![]() ).
В общем случае все корни, а значит и все
собственные частоты различные.
T1:
).
В общем случае все корни, а значит и все
собственные частоты различные.
T1:
![]() -
действительные:
-
действительные:
![]()
Т2 >0; (d+a)/2=p>0; Q=d(a-b)=df>0
![]()
1-й тон колебаний

2-й тон колебаний

Каждой собственной частоте соответствует определённая форма колебания, т.е. определённое соотношение между всеми амплитудными перемещениями
Произвольно задав одно из амплитудных
перемещений из уравнения можно найти
второе.
Пусть
 - опорные коэф-ты (как масштаб)
- опорные коэф-ты (как масштаб)
![]()
![]() -
коэф-т формы.
-
коэф-т формы.
Собственные формы колебаний показывают отношение м/д максимальными амплитудами при главных колебаниях при заданной частоте.
![]()
![]()

Собствен. Форма- величина безразмерная
А1 задаёт масштаб.
![]()
Главные нормальные координаты – координаты в которых кинемат. И потенц. Энергия представлены квадратичными формами в канонич.виде.

Переход к главным нормальным координатам.
Т.О главных формах колебаний. Переход к ГНК осуществляется заменой переменных:
![]()

![]()

Док-во:



![]()
![]()
 =>
=>

12. Основной параметрический резонанс в уравнении Матье. Границы области неустойчивости, решение и с.Д.У. Для амплитуды и фазы решения в первом приближении.
В некоторых случаях при периодически изменяющихся параметрах возникают нарастающие колебания системы, имеет место параметрический резонанс.
- основной параметрический резонанс.
- резонанс второго порядка..
и т.д.
![]() - уравнение Матье.
- уравнение Матье.

![]()


![]()

![]()
![]()
![]()
![]() -Коэф
при
-Коэф
при
![]() ;
;![]() -при
-при
![]() ;
;
![]() -всё
остальное.
-всё
остальное.
![]() ;
;![]() ;
;
![]()
![]()
![]()
найдём д.у и решения амплитуды и фазы.
![]()
![]() /2
/2
![]()
![]()
![]()
Граница области неустойчивости![]() =0;
=0;
![]() =0
=0
![]() =>
=>![]()
Замена Боголюбова
![]() =>
=>![]()
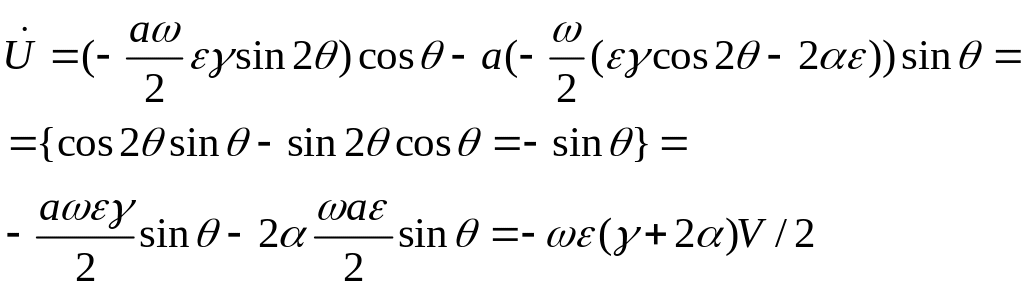
![]()
![]()
![]()
![]()
![]()
1)

![]()

2)
![]()
![]() ;a(t)->∞
При t→∞ t
пропорционально линейному закону,
причина в том,что мы взяли только первое
приближение.
;a(t)->∞
При t→∞ t
пропорционально линейному закону,
причина в том,что мы взяли только первое
приближение.
3)
![]()

![]()
13.Колебания систем с двумя степенями свободы. Случай нулевых и кратных собственных частот.
Случай нулевых частот

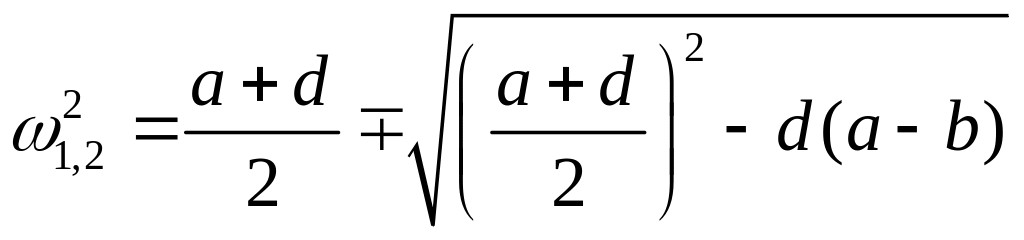
![]() ;
;
![]() ;
;
![]() ;
;
![]()
1)
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
2)
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Наличие нулевой собственной частоты говорит о том, что система может двигаться как жесткое целое.
Имеется КА состоящий из 2-х отсеков, соединенных фермой.

![]() ;
;
![]() ;
;
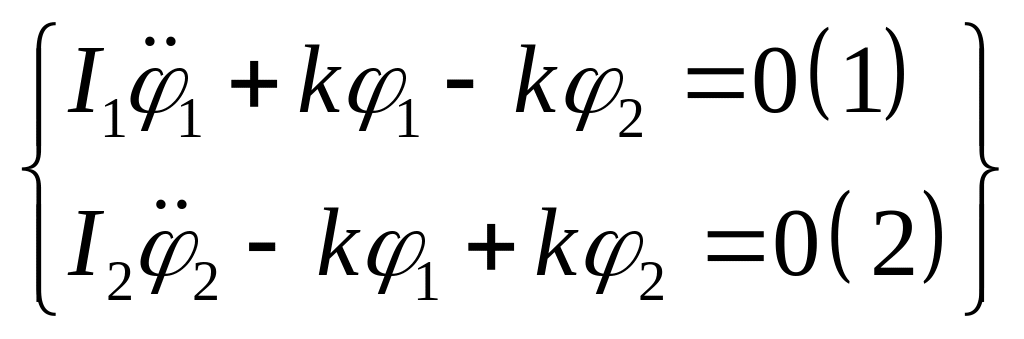 ;
;
![]()
![]()
![]()

![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]()
Случай кратных частот
2 степени свободы.
степени свободы.
Возможны 2 независимых движения: по ОХ и по ОУ.
![]()

![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]()
 ;
;

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() если
bd=0 b=0 d=0
если
bd=0 b=0 d=0
a=f
14. Метод последовательных приближений.
![]() (1)
малый
параметр
(1)
малый
параметр
![]() (2) – асимптотический ряд
(2) – асимптотический ряд
![]() ;
n – номер приближения
;
n – номер приближения
![]()
![]()
![]() невозмущенное движ-е
невозмущенное движ-е
![]()
![]()
![]()
![]()

![]()
15. Симпатические маятники
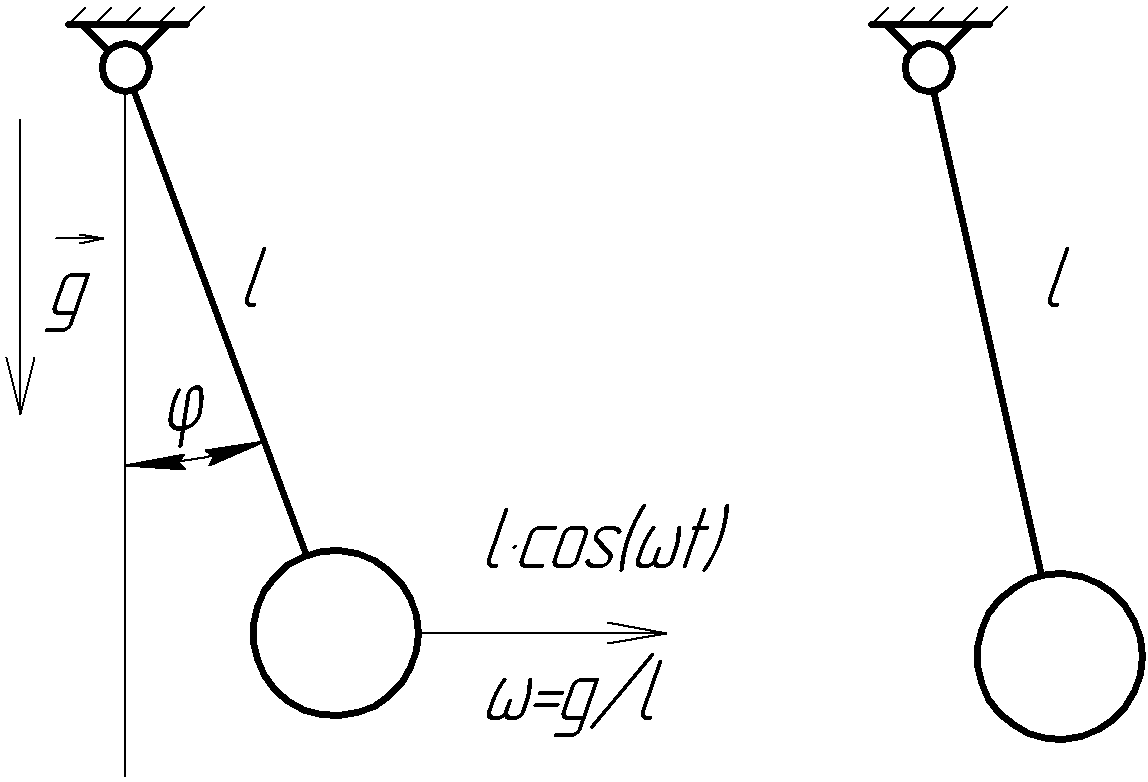
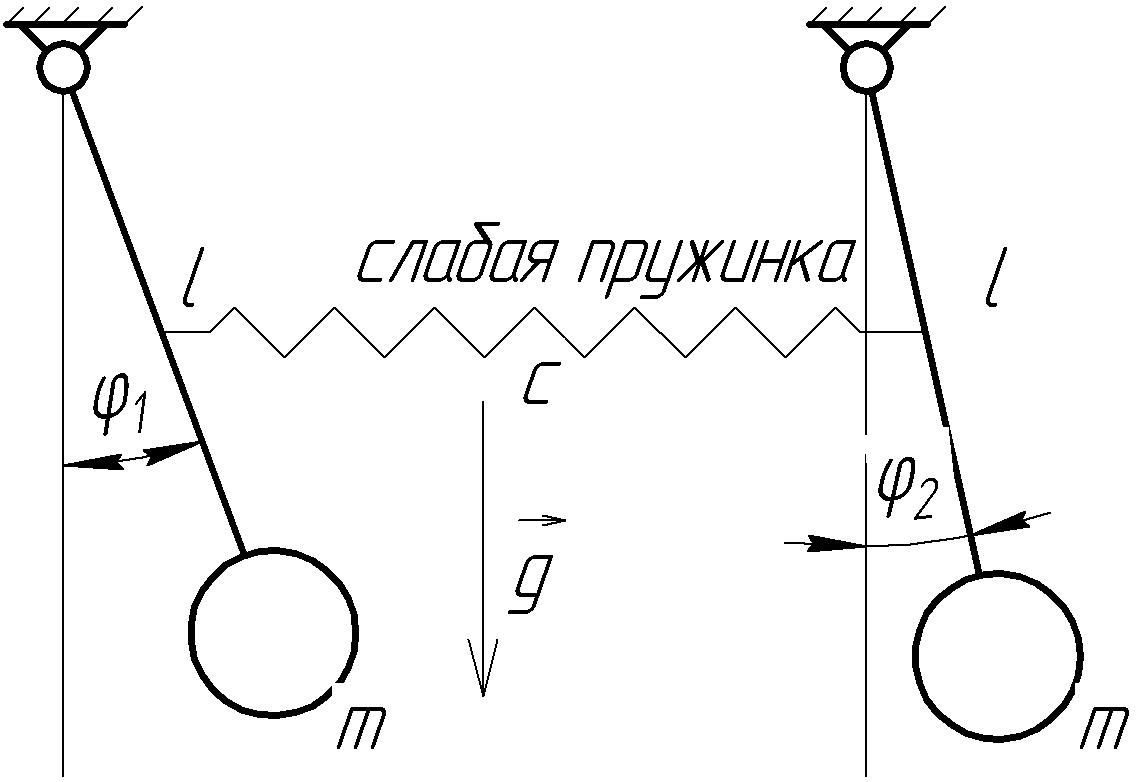


![]()
![]() ;
i=1,2
;
i=1,2
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
(1) - (2):
![]()
(1) + (2):

![]() ;
;
![]() ;
;
![]() ;
пусть
;
пусть
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
н.у. t=0
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()

16.Метод Пуанкаре на примере уравнения Матье в первом приближении.
(метод исследования параметрических колебаний)

α – частотная расстройка
Рассмотрим метод Пуанкаре на примере уравнения Матье:



![]()
![]()
Уравнение (*):
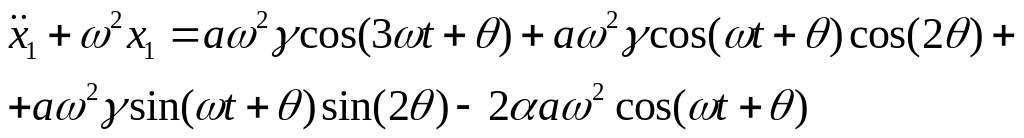 Коэффициенты
при резонансных слагаемых:
Коэффициенты
при резонансных слагаемых:
При
![]() :
:
![]()
При
![]() :
:
![]()
Возведём в квадрат и сложим:
![]()
![]()
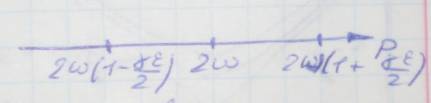
Пусть
![]() ,
подставляем в ур-е (*). Все резонансные
слагаемые обнуляются. В итоге получим:
,
подставляем в ур-е (*). Все резонансные
слагаемые обнуляются. В итоге получим:
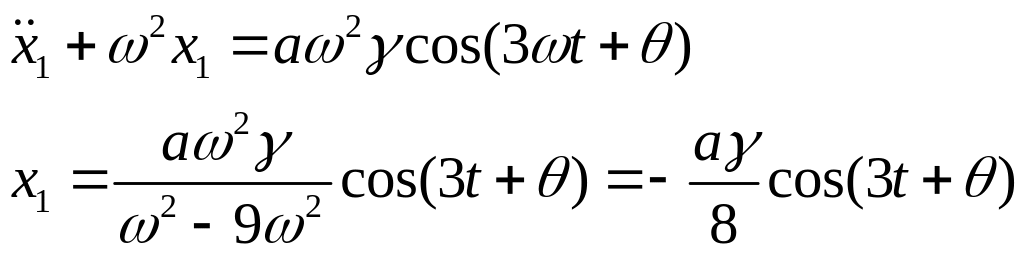
Тогда
![]()
17.Вынужденные колебания системы с двумя степенями свободы. Амплитудно-частотная характеристика.

Амплитудно-частотная характеристика системы с двумя степенями свободы.


18.Метод Релея.Метод Ритца.На примере балки постоянного сечения.
Метод Релея и метод Ритца относятся к приблежённым методам исследования колебания.
Метод Релея:
![]()
![]()
![]()
![]()

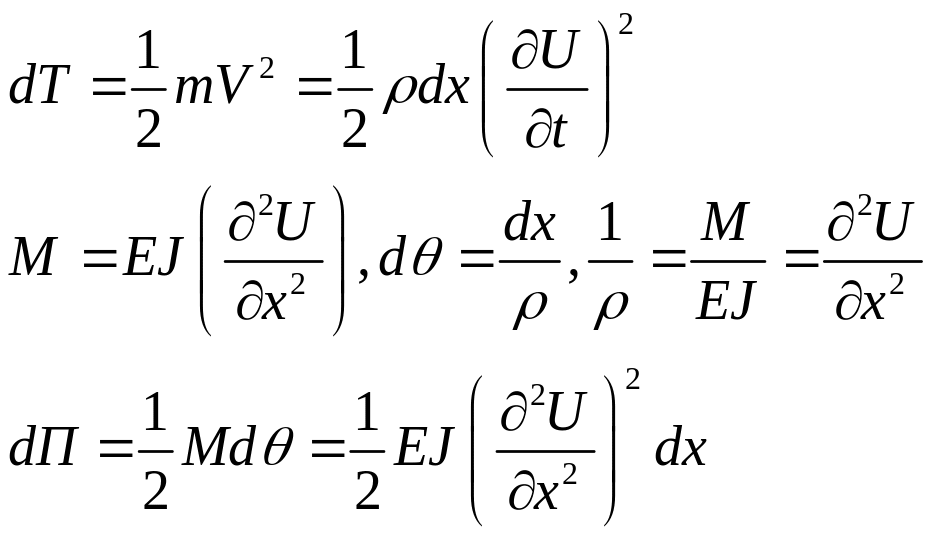

![]() ,
где
,
где
![]() -
необходимо задать такую, чтоб она
удовлетворяла кинематическим граничным
условиям.
-
необходимо задать такую, чтоб она
удовлетворяла кинематическим граничным
условиям.

Используем уравнение Лагранжа 2-го рода:
![]()
В результате получаем:
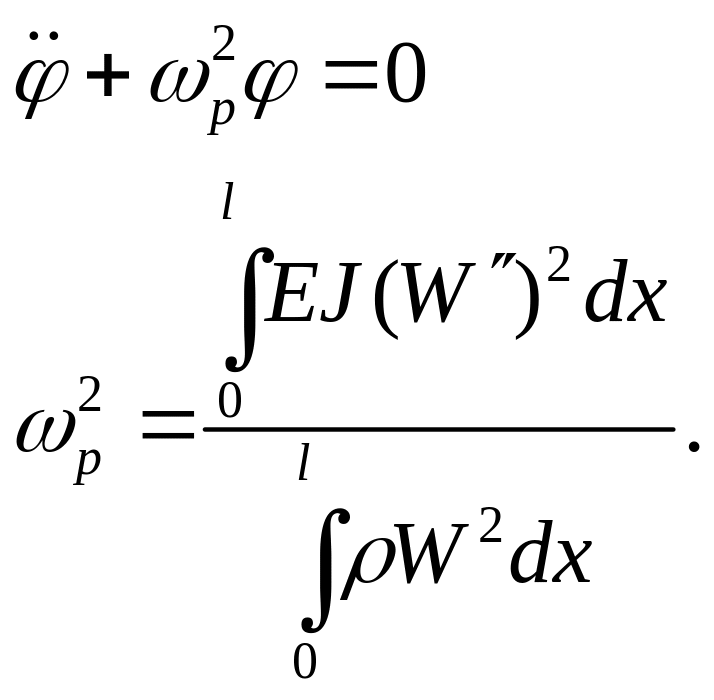
Теорема Релея:
![]() весгда
больше чем первая собственная частота
весгда
больше чем первая собственная частота
![]() .
.
![]() .
.
Пример:
Кинематические граничные условия:W(0)=0,W(l)=l.
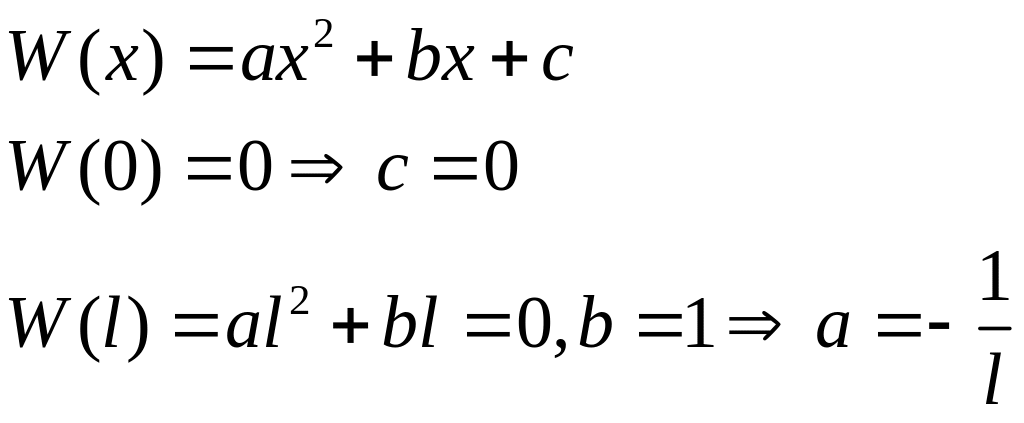
![]()

Силовые граничные условия:

Точное решение:
![]()
![]()
Метод_Ритца


![]()
![]()

![]() ,
где
,
где
![]() -
произвольная, удовлетворяющая
кинематическим условиям функция.
-
произвольная, удовлетворяющая
кинематическим условиям функция.
![]()

Пример:
![]() ,
,
![]()
![]()

![]()
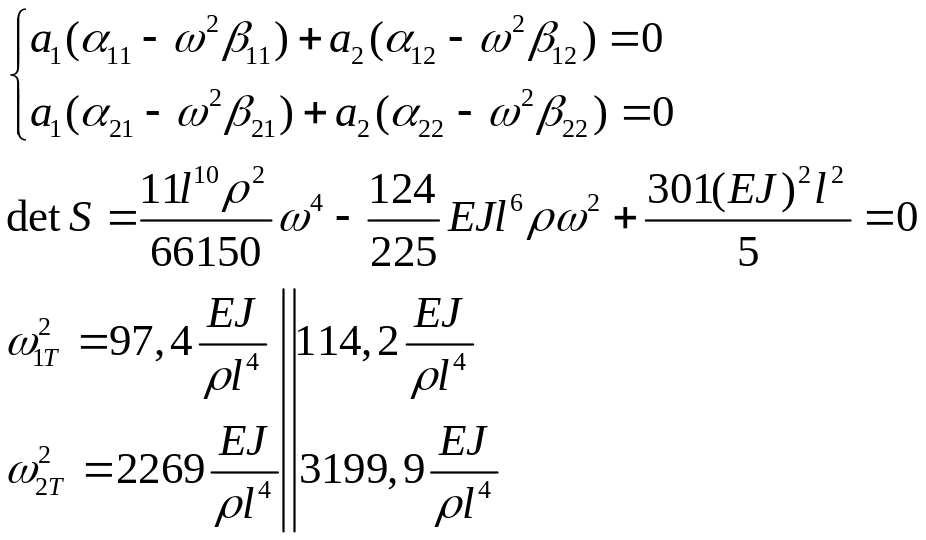
![]() 19.
Резонанс в системе с двумя степенями
свободы. Динамическое демпфирование.
19.
Резонанс в системе с двумя степенями
свободы. Динамическое демпфирование.

æ1=d/(d-ω21)>0;d> ω21; æ2=d/(d-ω22);d< ω22

Динамический демпфер
![]()

20. Определение крит. продольной нагрузки
для стержня в случае шарнирного
з![]() акрепления.
акрепления.
![]()
ω2>0 – устойчивость
ω2=0 – граница устойчивости
ω2<0 – неустойчивость

Пусть гр.у. – шарниры; E,J,ρ – const

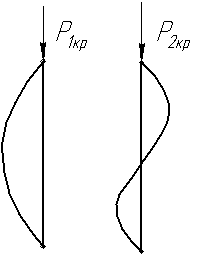 Граница
устойчивости.
Граница
устойчивости.
![]()
21. Колебание систем с конечным числом степеней свободы. Главные формы колебаний. Условия ортогональности.
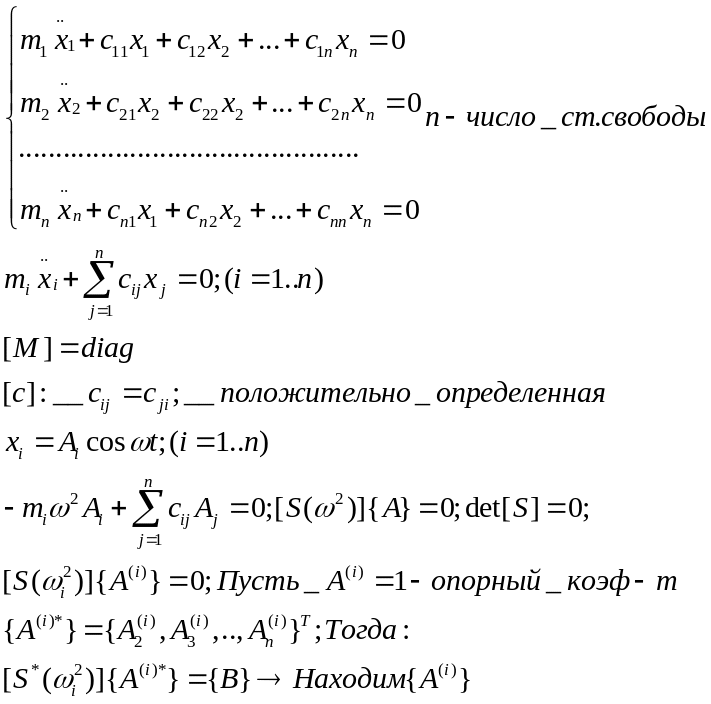
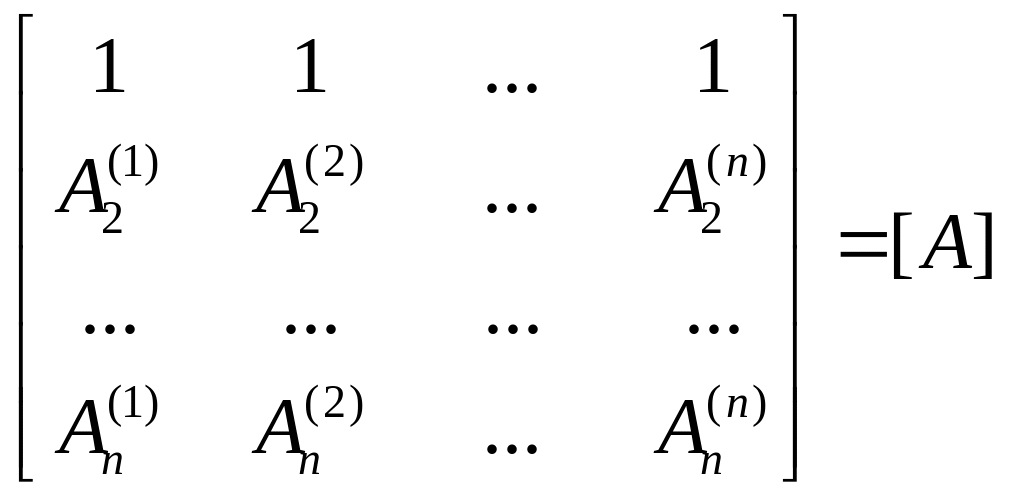
 Переход
к г.н.к.. Условия ортогональности.
Переход
к г.н.к.. Условия ортогональности.

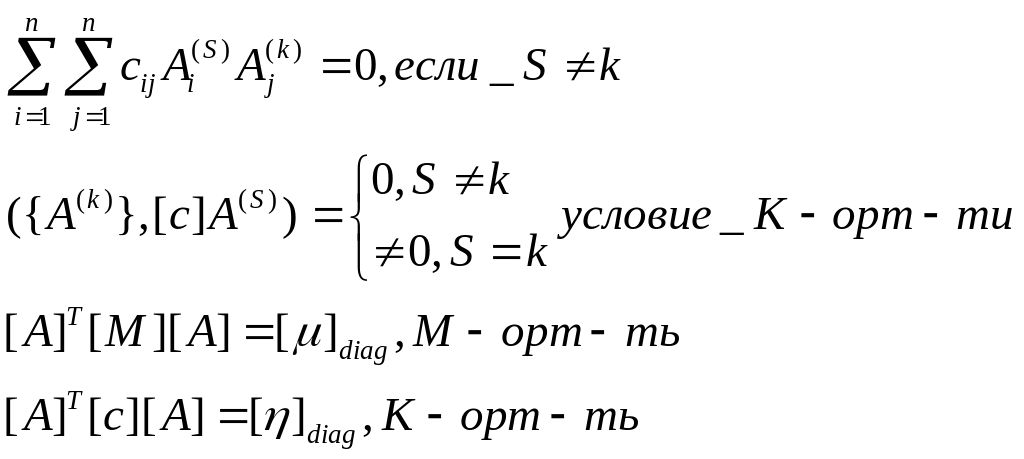
Применение условия ортогональности
![]()
Если известна м-ца [A], тогда {x}=[A]{φ}, где {φ} – вектор главных нормальных координат.

22.Поперечные колебания стержней постоянного сечения. Вывод уравнений, Граничные условия, Точное решение на примере консольно закрепленного стержня,

![]() ,
,
![]() ,
,
![]()
Плоское сечение
Проекция на ОУ:
![]()
![]()
![]()
![]() ,
,
![]() ,
,
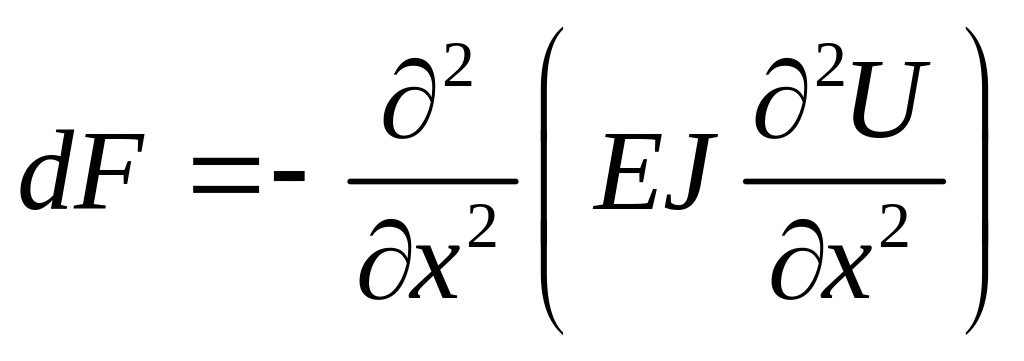
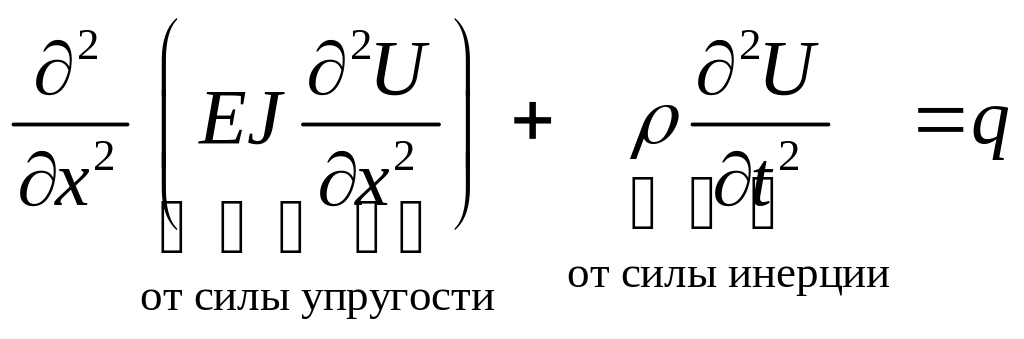 - уравнение поперечных колебаний
- уравнение поперечных колебаний
![]()
![]()
![]()
Начальные условия:
![]()
![]()
Граничные условия:
![]()
![]()
Кинематические:
![]() - прогиб;
- прогиб;
![]() - угол поворота сечения
- угол поворота сечения
Силовые факторы:
![]() - момент;
- момент;
![]() - поперечная сила
- поперечная сила
1![]() )
)
![]()
![]()
![]()
2![]() )
)
![]()
![]()
![]()
![]()
3 )
)
![]()
![]()
4)
![]()
Поперечные свободные колебания стержня постоянного сечения:
![]()
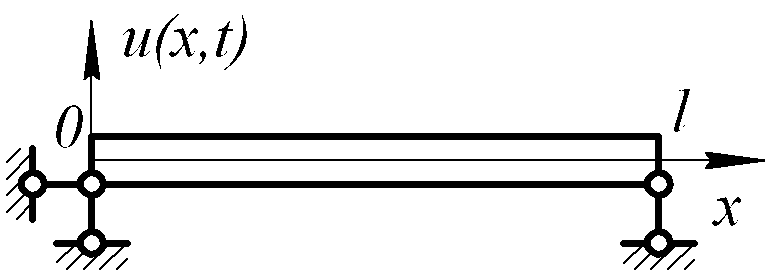 ,
,
![]()
![]() (1)
(1)
Начальные условия:
Граничные условия:
![]()
![]()
![]()
![]()
![]() (2)
(2)
(2)→(1)
![]()
1) Краевая задача
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
2) задача Коши
![]()
!
![]() !
– балочная функция
!
– балочная функция
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]() →
→![]() .
Тогда
.
Тогда
![]()

2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
