Лекция 5 1

Вычисление производных 1

Вычисление первой производной 1

Вычисление второй производной 2

Решение алгебраических уравнений 3

Метод деления пополам 3

Решение алгебраических уравнений методом Ньютона 6

Решение уравнения теплопроводности 7

Вычисление интегралов 12

Лекция 5 Вычисление производных Вычисление первой производной

Во многих случаях вычисление производных аналитически затруднительно или вовсе невозможно (если функция задана таблично). Тогда производная вычисляется приближенно или, как говорят, численно. В основе численного вычисления производных лежит разложение функции в ряд и ограничение этого ряда несколькими членами. В самом деле, если отрезок оси x, на котором задана наша функция, разбить на множество равноотстоящих точек {x_i}, то для каждой точки x_i можно записать разложение в ряд (здесь используются обозначения , f(x_i) = f_i, f(x_i+1) = f_i+1, f(x_i-1) = f_i-1):

Если мы вычтем из первого уравнения второе, то получим

откуда получаем

(1)

Эта формула называется формулой центральных разностей, поскольку вычисляет значение производной в центральной точке, используя значения функции в соседних точках, и позволяет вычислить значение производных с высокой степенью точности (порядка h²).

На Рис. 1 приведен пример вычисления производной функции f(x) = 1/(1 + x). Из приведенной таблицы видно, что погрешность численного метода весьма невелика даже при достаточно грубом выбранном нами шаге и падает с ростом x. Последнее обстоятельство вызвано тем, что погрешность, как следует из приведенных выше формул, пропорциональна третьей производной, а она для данной функции падает с ростом x.

Вычисление второй производной

Если мы не вычтем, а сложим два приведенных выше разложения функции в ряды, то получим

,

откуда получаем приближенное выражение для вычисления второй производной

, (2)

справедливое со вторым порядком O(h²) точности.

Вычисления согласно (2) подтверждают применимость этого выражения для приближенного вычисления вторых производных.

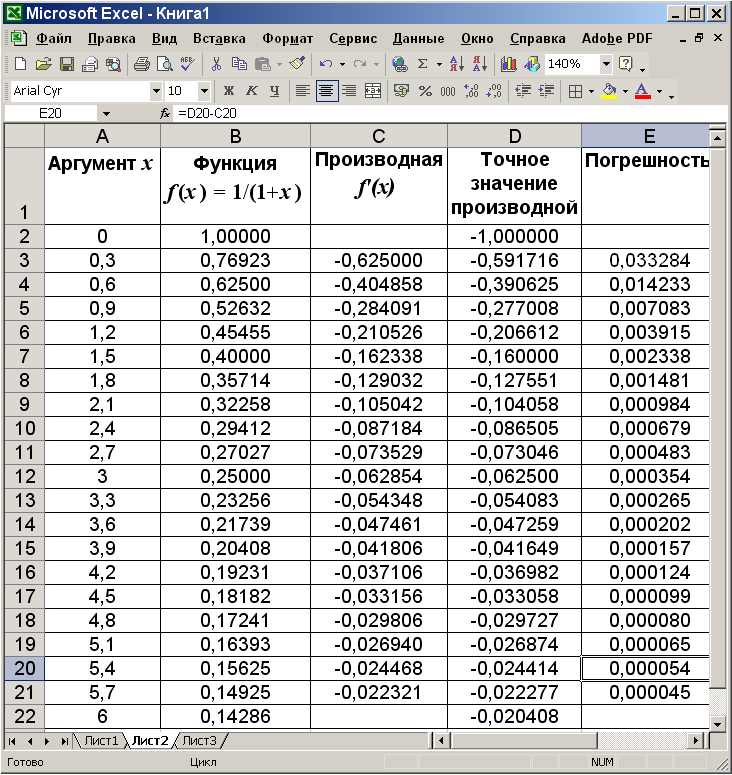
Рис. 1

Решение алгебраических уравнений Метод деления пополам

Не всегда можно (а точнее, почти никогда нельзя) найти решение алгебраического уравнения аналитически, т.е. выразить его на языке формул и найти корень точно. Поэтому на практике приходится искать приближенные значения корней уравнений. Для этого используются различные методы приближенных вычислений. Одним из самых простых и наглядных и вместе с тем эффективных является метод деления пополам. Суть метода состоит в следующем. Прежде всего, каким либо способом (например, графически) определяется интервал, на котором находится искомый корень. Непременным условием работоспособности метода является то, что функция на границах этого интервала имеет разный знак и, следовательно, корень находится между ними. Затем вычисляется значение функции в средней точке интервала. Знак функции в этой точке будет совпадать со знаком функции в одной из границ интервала. Это означает, что искомый корень находится на другой половине интервала. Именно она снова делится пополам и процедура повторяется до тех пор, пока не будет найдено решение с приемлемой точностью.

Рассмотрим реализацию метода на примере поиска корня уравнения e^x – x – 2 = 0. Известно, что искомый корень лежит в интервале [-2;-1] (см. рис.6).

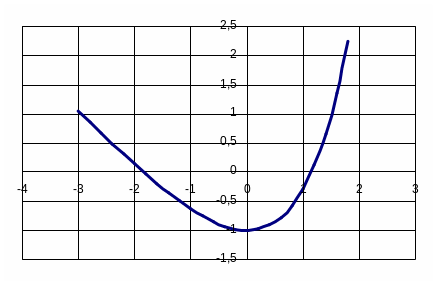
Рис. 2

Составим таблицу для решения задачи и заполним ее первую строку, что не составит труда (Рис. 3). В ячейку А8 поместим значение аргумента на левом краю интервала x = -2, а в ячейку С8 – значение на правом краю x = -1. В ячейке В8 поместим среднее значение, которое вычислим по формуле =(А8+С8)/2. Значение функции на левой границе вычислим в ячейке D8 по формуле =exp(A2)-A2-2, а скопировав эту формулу и вставив ее в ячейки E8 и F8, получим в этих ячейках значения функции в центре и на правой границе интервала.

Теперь начинается самое интересное. В ячейке А9 мы должны поместит координату новой левой границы интервала. Это или старая левая граница, или центр интервала, полученный делением его пополам. Выбор зависит от того, на какой половине интервала находится искомый корень. Если на левой – то левая граница остается, а если на правой половине – то центр интервала должен стать левой границей нового, половинного интервала. Как же определить, где находится корень? Исключительно просто: корень на той половине интервала, на которой функция имеет разные знаки на концах. Тогда в ячейке А9 должна быть записана формула =ЕСЛИ(ЗНАК(D8)=ЗНАК(Е8);В8;А8). Соответственно, в ячейке С9 должна быть записана формула =ЕСЛИ(ЗНАК(Е8)=ЗНАК(F8);В8;C8), т.е. при равенстве знаков функций на концах правой половины интервала в качестве правой границы теперь должен использоваться центр интервала, а при их неравенстве – остается прежняя правая граница. В ячейке В9 по-прежнему должна находиться формула половинного деления. Как видно из рис. 6, правая граница сместилась в строке 9 в точку -1,5, а центр имеет координату -1,75. В ячейки D9:F9 следует скопировать формулы из ячеек D8:F8. Теперь, чтобы следить за ходом вычислений, достаточно выделить ячейки A9:F9 и распространить находящиеся в них формулы маркером заполнения на нужное количество строк вниз. Результат показан на Рис. 3.

Распространив исходную строку достаточно далеко, мы всегда можем найти корень с заданной точностью, которая, к тому же, визуально контролируется. Однако такой способ не является самым удобным и компактным. Намного удобнее было бы автоматизировать повторение вычислений до тех пор, пока не будет достигнута заданная точность. Excel позволяет легко реализовать и такой подход. Для этого необходимо проделать ту же процедуру, что и в предыдущем примере, но (рис. 8) после заполнения ячеек A32:C32 поступить несколько иначе: вернуться к ячейке А31 и записать в ней формулу =А32, а в ячейке С31 записать формулу =С32. Теперь значения в ячейках А31 и А32 оказались замкнуты друг на друга через ячейку D31, а в ячейках С31 и С32 через F31 (Рис. 4).

Однако для того, чтобы циклические вычисления выполнялись, необходимо предпринять специальные усилия. В меню Сервис | Параметры на вкладке Вычисления необходимо установить флажок Итерации и указать предельное число шагов итерационного процесса (установленное по умолчанию число шагов 100 явно недостаточно во многих случаях) и относительную погрешность, по достижении которой вычислительный процесс остановится. Без этих ограничений циклический вычислительный процесс никогда бы не остановился. Как видно из Рис. 4., решение задачи в случае организации циклических вычислений выглядит намного более компактным, чем в предыдущем случае.

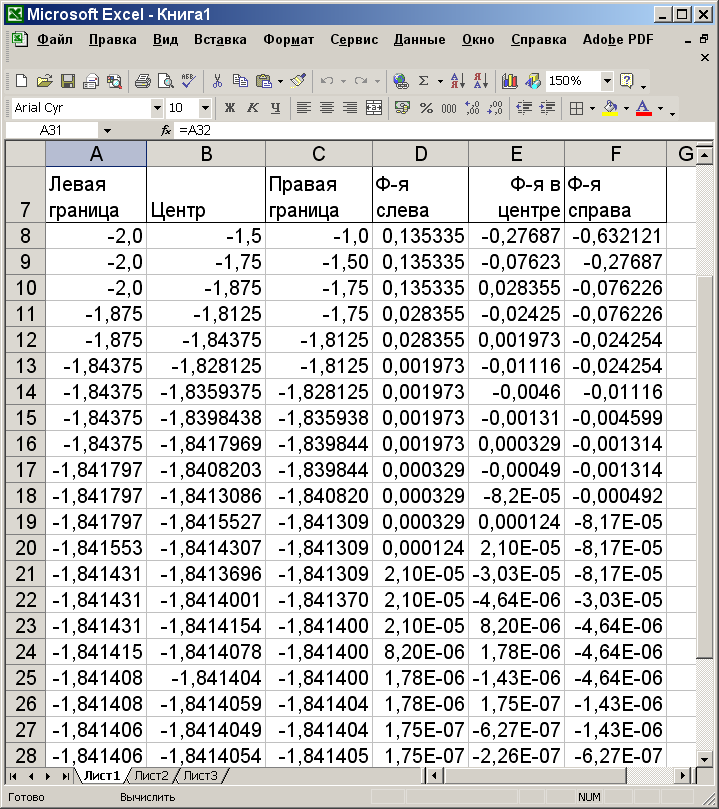
Рис. 3

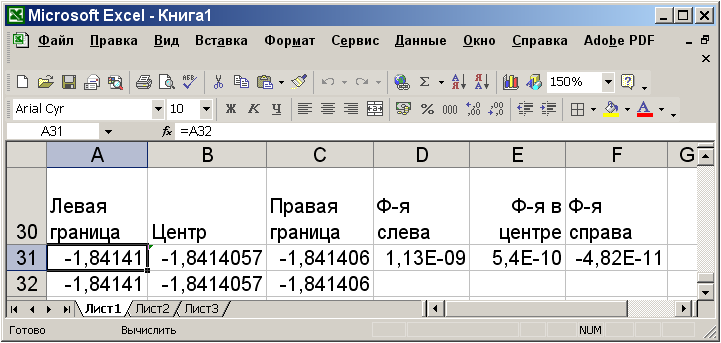
Рис. 4