1.4 Сопротивление зернистой шероховатости. Коэффициент шероховатости

Развитие гидравлики русловых потоков шло прежде всего в направлении поиска зависимости коэффициентов, учитывающих гидравлическое сопротивление, от характера шероховатости дна, т.е. от величины относительной шероховатости (Δ/Н или d/H) или относительной гладкости (H/Δ или H/d).

Первая попытка определить коэффициент Шези с через шероховатость русла была предпринята А.Дарси и П. Базеном в 1855-1862 гг. На основе экспериментов в каналах и лабораторных лотках была получена формула, связывающая C с коэффициентом , характеризующим шероховатость русла. Позже (1897) Базен опубликовал новую, ставшую более известной, формулу

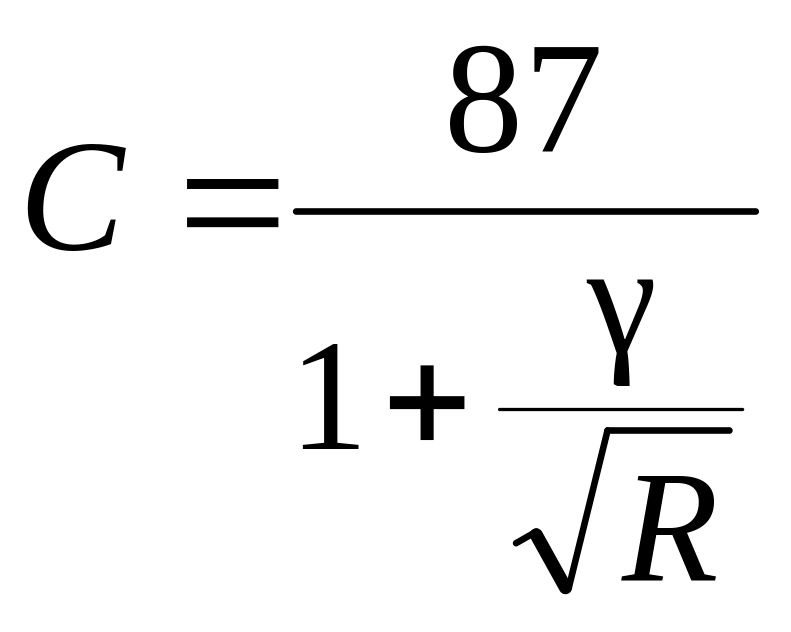, (1.11)

где R – гидравлический радиус. Численные значения коэффициента  находятся в диапазоне от 0,06 (русла с очень гладкими стенками) до 1,75 (земляные очень шероховатые русла).

В 1869 г. швейцарские инженеры Е.Гангилье и В.Куттер после обработки огромного материала по рекам и каналам (в том числе и данных Дарси-Базена) предложили формулу

, (1.12а)

где n – коэффициент шероховатости, отличный от коэффициента  в формуле Базена. При уклонах I0,0005 влияние члена 0,00155/I становится малым и им можно пренебречь. В этом случае формула Гангилье-Куттера упрощается:

. (1.12б)

Диапазон изменения коэффициента n в упомянутой формуле – от 0,008 (лоток из строганых досок) до 0,056 (канал с каменистым дном). Считают, что термин коэффициент шероховатости был впервые употреблен именно Гангилье и Куттером.

Несмотря на громоздкость, формула Гангилье-Куттера использовалась вплоть до начала ХХ в., пока она не была вытеснена более простой и надежной формулой, предложенной в 1889 г. ирландским инженером Р. Маннингом:

. (1.13)

Эта формула широко используется и в наши дни. При этом часто гидравлический радиус R заменяют на среднюю глубину Н.

Сходную структуру имеют формулы Ф.Форхгеймера (1923) и Н.Н.Павловского (1925). По Форхгеймеру, показатель степени у R равен 1/5. Формула Павловского имеет вид

. (1.15)

В последней формуле в отличие от формул Маннинга и Форхгеймера показатель степени переменный, зависящий от n и R: . При R1 м y1,5 , при R1 м y1,3 .

В формулах (1.12)–(1.15) коэффициент шероховатости n – один и тот же. Он зависит от характера русла и изменяется от 0,008 для лотков с исключительно гладкими стенками до 0,040 для рек и каналов с плохими условиями (русла заросшие, с неровным дном) и до 0,20 для заросших речных пойм. Значения коэффициента шероховатости n можно найти в таблицах, составленных Н.Н.Павловским, М.Ф.Срибным, Б.В.Поляковым, И.Ф.Карасевым, В.Т.Чоу и др.

Недостаток всех приведенных формул – неопределенность в количественной оценке величины коэффициента шероховатости n.

Первая попытка придать количественный смысл коэффициенту n предпринял гидравлик Р.Мазес (1914 г.). Он ввел понятие высоты выступов шероховатости  и для труб получил зависимость вида n=f(/D), где D – диаметр трубы, а /D – относительная шероховатость.

Для открытых русел аналогичный подход применил А. Штриклер в 1923 г. Он связал коэффициент шероховатости n со средней крупностью частиц грунта, слагающего дно (d):

, (1.16)

где d в м.

Подстановка (1.16) в формулу Маннинга (1.13) дает такое выражение для коэффициента Шези:

. (1.17)

По данным К.В.Гришанина (1979), эта формула Маннинга–Штриклера широко применяется в инженерных расчетах.

Известна также другая попытка связать n и d, предпринятая Чангом:

, (1.18)

где d в мм.

Основываясь на формуле Чанга, М.А.Великанов (1958 г.) формулу Шези–Маннинга представил в виде

, (1.19)

где d в м. Эту формулу с полным основанием можно назвать формулой Шези–Маннинга–Чанга–Великанова.

Интересна попытка связать n и С с крупностью донных наносов, предпринятая В.М.Маккавеевым и А.В.Караушевым. Их формулы имеют вид

n=0,03d^1/6, (1.20)

, (1.21)

В этих формулах d – в мм. Формула Шези–Маннинга в интерпретации Маккавеева и Караушева получает вид

. (1.22)

Если же эту формулу записать в виде, аналогичном (1.19), и d выразить в м, то получим

. (1.23)

Как можно видеть, в формулах (1.17), (1.19) и (1.23) коэффициент перед С разный, что объясняется различием в числовых коэффициентах в связях n=f(d).

Важное исследование влияния зернистой шероховатости на русловой поток предпринял В.Н.Гончаров (1954, 1962). Коэффициент Шези выражен им через относительную гладкость Н/ и n уравнением типа формулы Маннинга:

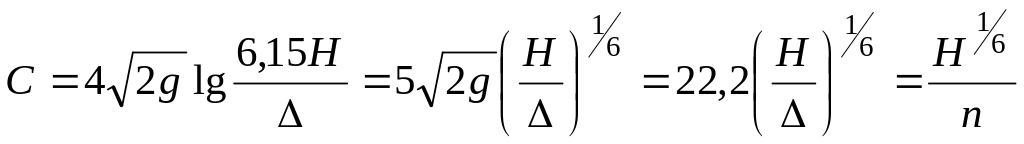. (1.24)

Здесь использована аппроксимация . Высота выступов шероховатости  для естественных грунтов дна связана, по Гончарову, с диаметром частиц наносов соотношением

=0,7d. (1.25)

Формула Шези в интерпретации В.Н.Гончарова приобретает вид

. (1.26)

Используя выше приведенные замены, получим формулу Шези в аналогичном (1.19) и (1.23) виде:

. (1.27)