Описание установки

Генератор синусоидального напряжения, электронные вольтметры V1 и V2 и фазометр работают от сети переменного напряжения. Их зажимы «Земля» должны быть соединены между собой. В связи с этим вольтметрами V1 и V2 можно измерять напряжение между любой точкой цепи и общей точкой соединения всех перечисленных выше приборов. Вольтметр V3 не связан с сетью переменного напряжения. Им можно измерять напряжение между любыми точками исследуемой электрической цепи. Фазометр показывает разность между фазами напряжений, подаваемых на зажимы «Сигнал» и «Опора».

Выполнение работы

1. Определить величину сопротивления резистора R, подключив его к источнику постоянного напряжения Е1.

2. Исследование режима в цепи RC. Собрать цепь по схеме на рис. 4.1. Установить частоту и напряжение U₁ на входе согласно заданию. Записать в табл. 4.2 показания приборов. Величину тока определить косвенным способом: I=U_R/R. Экспериментальную величину комплекса входного сопротивления Z_вх=ze^jφ рассчитать на основании показаний приборов: модуль z=U₁/I, а фаза  - показание фазометра с противоположным знаком. Сравнить результаты эксперимента с расчетом. Убедиться, что напряжение источника U₁ равно геометрической сумме напряжений на емкости и резисторе.

3. Исследование режима в цепи RL. Заменить конденсатор (схема на рис. 4.1) катушкой индуктивности. Выполнить измерения и расчеты, аналогичные для цепи RC. Результаты занести в табл. 4.3.

4. Исследование режима в цепи RLC. Собрать цепь по схеме на рис. 4.2. Записать в табл. 4.4 показания приборов и расчетов, выполненных на основе этих показаний. Изменяя частоту источника, добиться изменения характера входного сопротивления, наблюдая за показаниями фазометра: фазометр будет показывать фазы с противоположным знаком.

Контрольные вопросы

1. Как связаны между собой мгновенные значения токов и напряжений на элементах R, L, С?

2. Записать выражения для комплексного сопротивления индуктивности и емкости.

3. Записать выражения для перехода от показательной формы записи комплексного сопротивления Z к алгебраической, также обратного перехода от алгебраической формы к показательной.

12

4. Дать полное название следующим величинам:

i, , , , ; u, , , , , z, , R, X.

5. Определить показание приборов в схеме, заданной преподавателем.

6. Построить качественно векторную и топографическую диаграммы для схемы, заданной преподавателем.

Приложение 2

Теоретическая часть

Расчет режима цепи синусоидального тока (пп. 3,4,5) проводят символическим методом (методом комплексных величин) при строгом соблюдении стандартных обозначений. Все методы расчета режима в цепях постоянного тока справедливы для расчета режима в цепях синусоидального тока, если использовать комплексы амплитудных или действующих значений напряжений, токов, потенциалов, комплексы сопротивлений или проводимости.

При расчете режима цепи (пп. 3,4,5) осуществляют переход к комплексу действующего значения источника энергии. Вычисляют комплексные сопротивления элементов схемы. Методом свертки находят комплексное входное сопротивление, комплексы тока и напряжений на элементах. Приборы (вольтметр и амперметр) показывают действующие значения искомых величин.

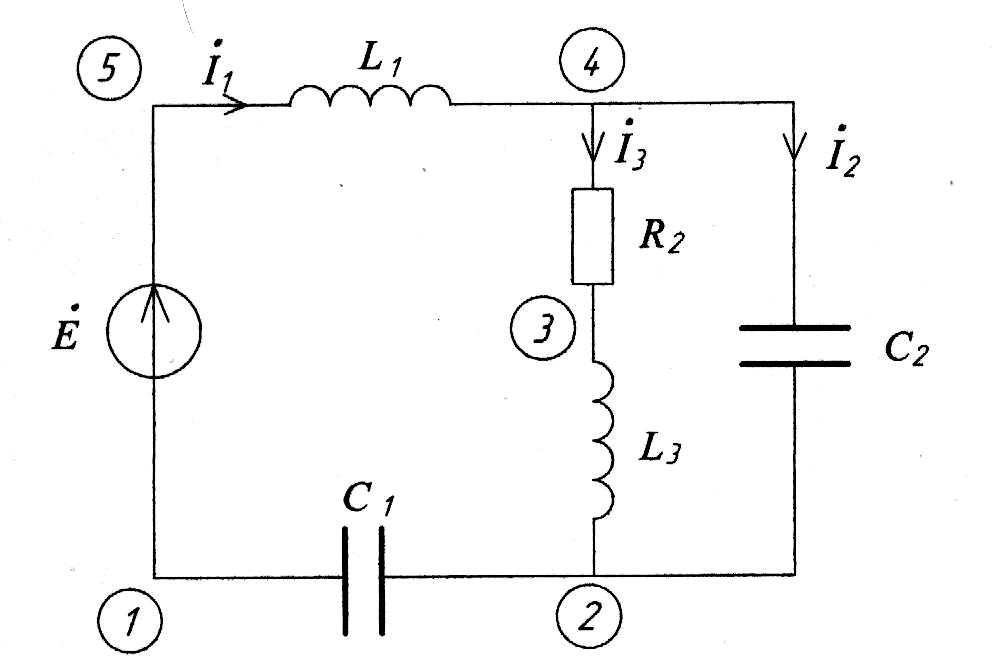
Пример определения показаний приборов в схеме на рис. 4.3.

Дано: E=10 В, =-30, R1=R2=200 Ом, C=5*10^-8 Ф, L=10^-3 Гн, =10⁵ 1/c.

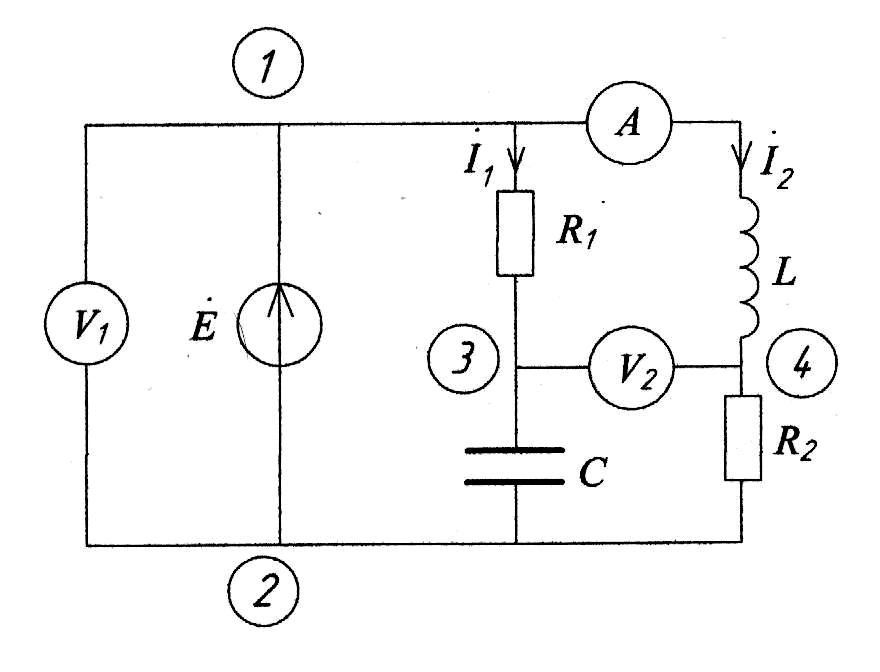
Рис. 4.3

13

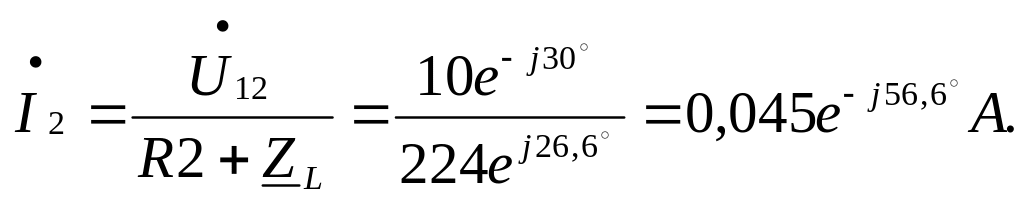
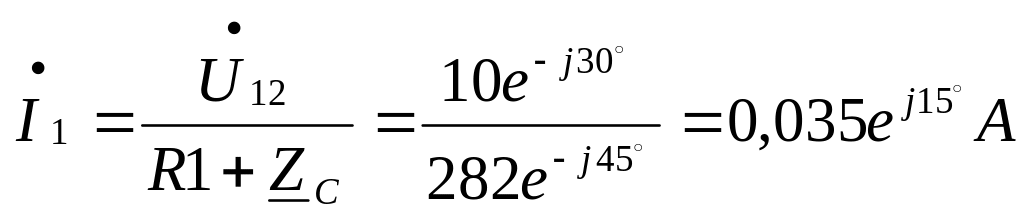
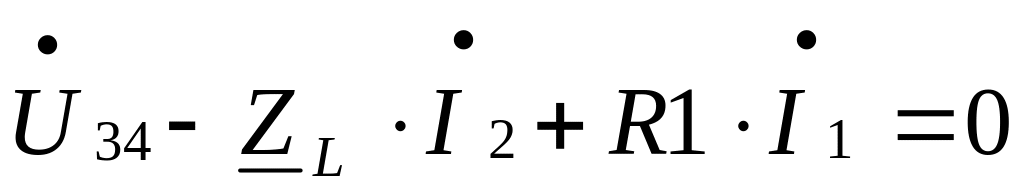
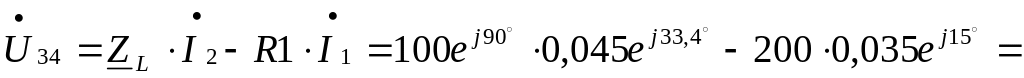
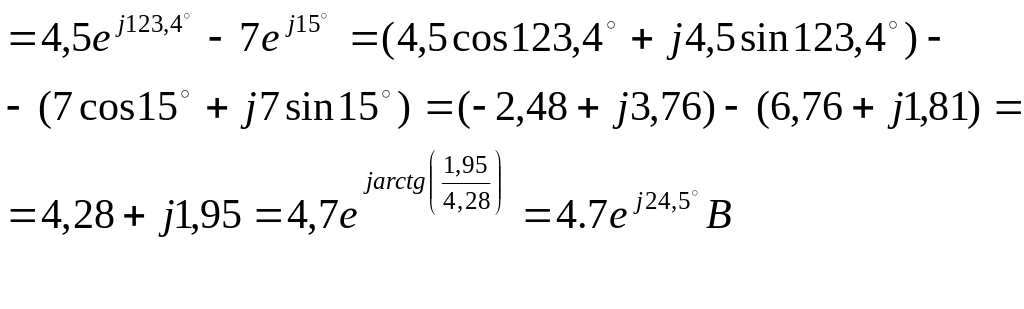
Приборы покажут: вольтметры U₁₂ =10 В, U₃₄ =4,7 В,

амперметр I₂=0,045 A = 45 мA.

Построение векторной и топографической диаграмм качественно возможно только для схем с одним источником.

Примерный порядок построения (см. рис. 4.4).

1. На схеме выбирают направление тока ветвей.

2. Схему разбивают на участки, содержащие по одному элементу. Точки, соответствующие концам этих участков, нумеруют.

3. Из начала комплексной плоскости произвольно изображают вектор тока самой удаленной от источника и нагруженной ветви.

4. Один из узлов этой ветви принимается за точку, потенциал которой считается равным нулю, и помещается в начало комплексной

14

плоскости. Обычно это узел, в который входят большинство токов.

5. Построение ведется по возможности против направления тока, так как это направление возрастания потенциала. На диаграмме последовательно откладывают и обозначают векторы напряжений на всех элементах самой удаленной от источника и нагруженной ветви с учетом закона Ома. Указывают номер потенциала соответствующей точки схемы.

6. Определяют напряжение между узлами ветви с учетом второго закона Кирхгофа.

7. Неизвестный вектор тока параллельной ветви находят по известному вектору напряжения ветви с учетом закону Ома.

8. Неизвестные векторы тока других ветвей определяют с учетом первого закона Кирхгофа или закона Ома.

9. Последовательно строят векторы напряжения на элементах всех контуров и векторы токов ветвей.

10. Топографическая диаграмма каждого контура и схемы должна быть замкнутой. Векторная диаграмма токов для каждого узла схемы должна подчиняться правилу параллелограмма.

Примечание.

Если строят вектор напряжения при движении по току, то на комплексной плоскости отдельно изображают вектор тока через этот элемент. Определяют положение относительно него вектора напряжения. Обозначают концы вектора напряжения с учетом того, что диаграмму строят против направления тока, т.е. начало вектора - точка с меньшим потенциалом, конец - точка с большим потенциалом. Найденный вектор напряжения переносят параллельно самому себе до совпадения с положением своей известной точки.

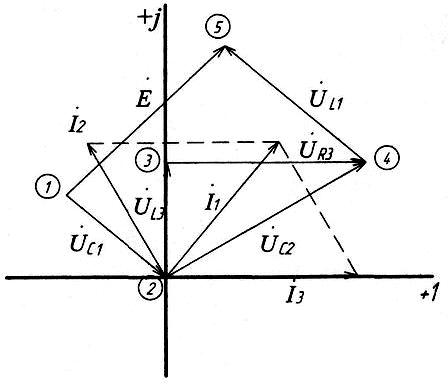Пример построения векторной и топографической диаграмм качественно (рис. 4.4)

Рис. 4.4

15

= + = = .

На комплексной плоскости известно положение и . Из точки 2 комплексной плоскости строят произвольной длины вектор , который повернут на 90 против часовой стрелки относительно вектора .

Аналогично, = + = + .

Согласно второму закону Кирхгофа находят :

- - =0; = + ,

как геометрическая сумма векторов и .

Тогда

.

Значит, вектор тока повернут на 90^о против часовой стрелки относительно вектора . Вектор выходит из той же точки комплексной плоскости что и , т.к. он входит в уравнение по первому закону Кирхгофа: + - =0. Отсюда геометрически находят вектор тока : + .

Определяют положение точки 5:

= + = + = + .

Значит, вектор выходит из точки 4 и повернут на 90 против часовой стрелки относительно вектора тока .

16

Находят положение точки 1:

= = ( ).

Строят отдельно = = . Вектор повернут на 90^о по часовой стрелке относительно вектора и имеет свою длину. Начало вектора - в точке, куда ток входит (точка  1), конец вектора - в точке, откуда выходит (точка 2).

Положение точки 2 на комплексной плоскости определено. Тогда вектор переносят параллельно самому себе до совпадения с точкой 2. Начало вектора определяет положение точки 1. Вектор получится, если соединить точку 1 с точкой 5.

Библиографический список

1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. М.: Гардарики, 2002. 639 с.

2. Немцов М. В. Электротехника и электроника. М.: МЭИ, 2003. 596 с.

3. Попов В.П. Основы теории цепей. М.: Высш. школа, 2003. 575с.

4. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. 5-изд., перераб. М.: Энергоатомиздат, 1989. 527 с.