3.2. Метод наименьших квадратов

В данном пункте рассматривается идея основного (для количественных факторов) метода обработки результатов эксперимента с целью получения математического описания объекта – метода наименьших квадратов. Для простоты рассмотрим случай варьирования единственного фактора . Предположим, что эксперимент состоит в постановке опытов, и в этих опытах фактор принимает значения . Здесь значение фактора в опыте номер , . Выходная величина принимает в этих опытах значения соответственно. Отложим по оси абсцисс значения фактора , принимаемые им в опытах, а по оси ординат – соответствующие значения , получим совокупность точек (рис. 3.3). Цель эксперимента – получение регрессионной зависимости , которая с достаточной точностью описывала бы результаты эксперимента.

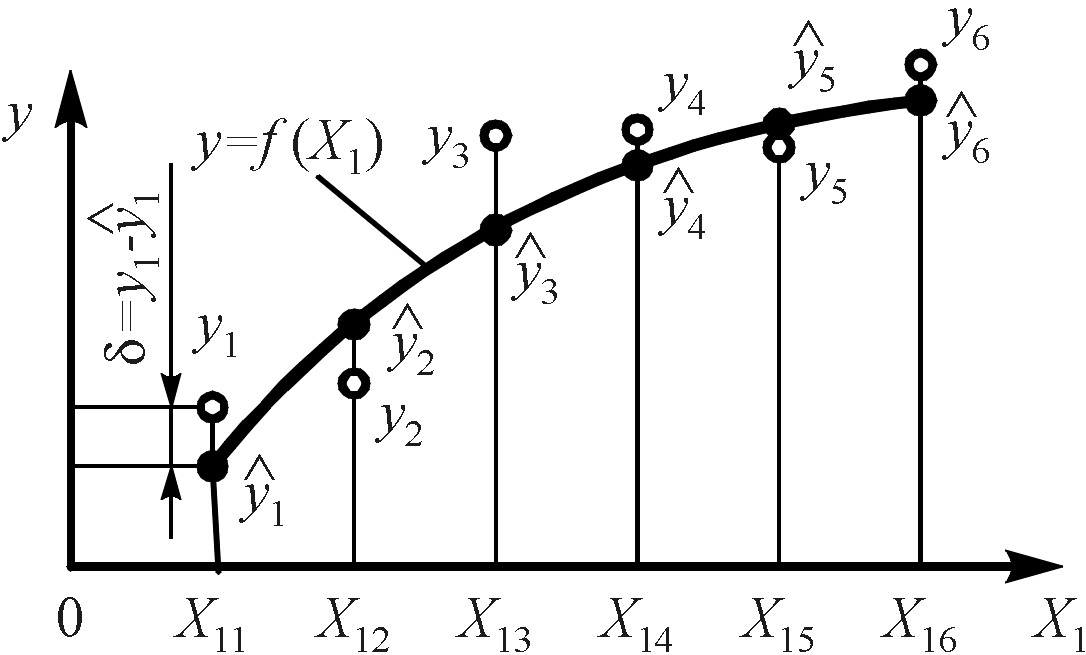
Рис. 3.3. Пояснение метода наименьших квадратов

Пусть требуется исследовать зависимость износа режущего инструмента от продолжительности резания. Износ оценивается радиусом затупления режущего лезвия . Тогда точки на рис. 3.3 – это значение , соответствующее разным значениям продолжительности резания. Закономерность изменения износа в зависимости от продолжительности резания получим на графике, если проведем гладкую кривую, лежащую возможно ближе к экспериментальным точкам. Однако на глаз такую кривую можно провести разными способами и, кроме того, помимо графика хотелось бы получить аналитическое представление для исследуемой зависимости. Все это заставляет обратиться к аналитическим методам построения регрессионной модели.

Конкретизируем приведенное выше требование, чтобы экспериментальные точки лежали в совокупности как можно ближе к кривой, являющейся графиком искомой зависимости. Допустим, что аналитическое представление зависимости от уже каким-то образом получено в виде уравнения регрессии . График зависимости – это искомая кривая (рис. 3.3).

Значениям фактора , равные соответствуют точки на кривой . Эти точки являются значениями выходной величины, рассчитанными по уравнению регрессии .

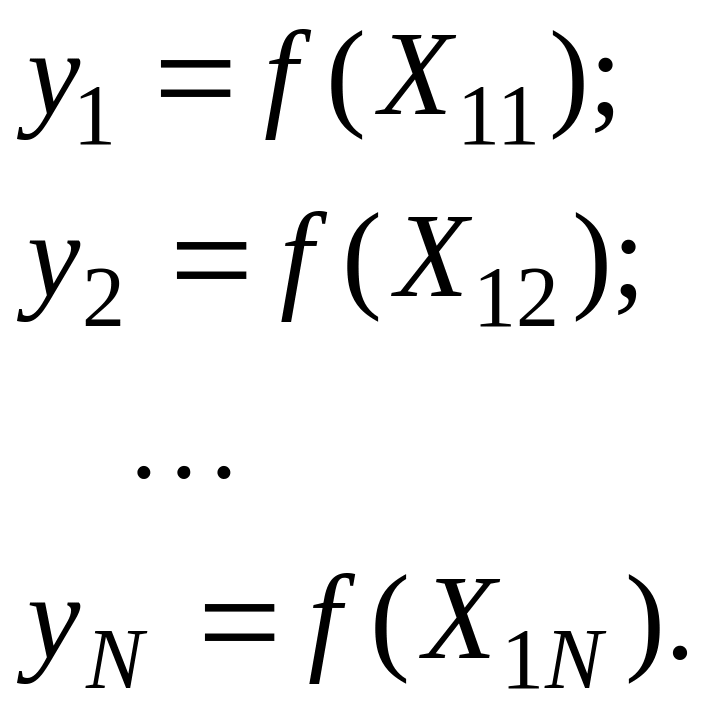(3.4)

Найдем величину равную (рис. 3.3), которая характеризует отклонение результата эксперимента в точке от значения функции отклика в этой же точке. Аналогично рассмотрим отклонения .

Согласно методу наименьших квадратов (сокращенно МНК), оценки для коэффициентов регрессии отыскиваются из условия минимума суммы квадратов отклонений , т. е.

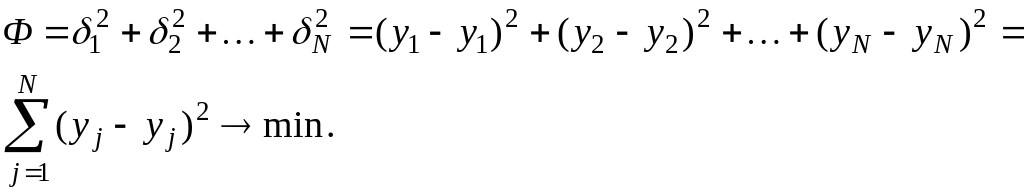(3.5)

В настоящее время для статистических расчетов (в общем) и для получения уравнений регрессии (в частности) с помощью персонального компьютера, широко используется специализированный пакет фирмы

3.3. Об интервале съема данных и продолжительности пассивного эксперимента

При проведении пассивного эксперимента и, в частности, в процессе наблюдения над промышленными объектами возникает вопрос об интервале съема данных и необходимой продолжительности всего эксперимента. Обозначим через временной интервал между последовательными измерениями выходной величины эксперимента. В предположении, что изменения исследуемой выходной величины во времени представляют собой стационарный случайный процесс, интервал съема данных можно определить из условия некоррелированности наблюдений. Для расчета надо иметь диаграмму изменений за некоторое время . По ней подсчитывают число пересечений диаграммой линии среднего значения за время . Вычисляют среднее число пересечений за единицу времени по формуле . Тогда искомую величину интервала съема данных отыскивают из условия:

(3.6)

Считается, что для определения достаточно взять интервал времени , в течение которого получено 40 – 70. Нецелесообразно выбирать величину , превышающую значение из-за возможных изменений внешних условий, параметров объекта и т. п.

При оценке времени наблюдения над выходной величиной, т. е. продолжительности пассивного эксперимента предлагается руководствоваться требованием, чтобы за это время наблюдаемая переменная успела пройти весь диапазон своего изменения с некоторой заданной вероятностью . Предположим, что весь диапазон изменения выходной величины разбит на ряд одинаковых интервалов в соответствии с разрешающей способностью измерительного прибора и известна вероятность попадания величины в верхний и нижний интервал диапазона. Величину берут обычно из отчетных данных. Продолжительность эксперимента определяют по формуле

(3.7)

где интервал съема данных; параметр, определяемый в зависимости от заданной вероятности по формуле . Укажем, что для типичных значений 0,95, 3,68; для 0,99; 5,3.

Формулы (3.6) и (3.7) можно использовать не только для определения временных интервалов, связанных с продолжительностью съема данных, но и для расчета других физических величин, характеризующих объем проводимого пассивного эксперимента.