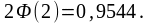- •Конспект лекцій з курсу « Теорія ймовірності та випадкові процеси» Розділ 1 Вступ. Поняття ймовірності.
- •Коротка історична довідка.
- •Непарні
- •Властивості ймовірності подій
- •2. Основні формули комбінаторики.
- •Статистичне визначення ймовірності подій
- •1. Для лінійного випадку
- •2. Для плоского випадку
- •1.Умовна ймовірність.
- •Л) незалежні події. Теорема множення незалежних подій.
- •Часто ймовірність події ā позначають
- •0) Наслідки із додавання і множення.
- •1)Теорема додавання ймовірностей сумісних подій.
- •Р(в) – ймовірність попадання другого.
- •Розділ 2: послідовності незалежних випробовувань. Формула бернуллі
- •Вивід формули Бернуллі:
- •Б) Локальна теорема Лапласа (без доведення)
- •Розділ 3. Основні поняття математичної статистики. Випадкові величини та їх числові характеристики. А. Поняття випадкової величини. Дискретні та неперервні випадкові величини.
- •В. Приклади: біноміальний закон розподілу. Закон розподілу Пуассона.
- •1) Біноміальний закон.
- •2) Розподіл Пуассона.
- •Г. Інтегральна та диференціальна функції розподілу випадкової величини, їх властивості та функція розподілу (крива розподілу).
- •Математичне сподівання та дисперсія випадкових величин.
- •Математичне сподівання має властивості:
- •Властивості дисперсії.
- •Сталий множник можна виключити
- •Якщо ξ: η- незалежні випадкові величини, то
- •Моменти к-того порядку.
- •Є. Ймовірність попадання випадкової величини в заданий інтервал. Нормальний закон розподілу неперервної випадкової величини
- •Правило трьох „σ”.
- •Ж. Поняття про функції випадкового аргументу і її закон розподілу.
- •Дискретна випадкова величина.
- •Неперервні випадкові величини
- •З. Закон великих чисел. Нерівність Чебишева , теореми Чебишева та Бернулі. Поняття про теорему Ляпунова.
- •Теорема Бернулі.
- •Теорема Ляпунова. (Поняття).
- •Теореми Чебишева, Бернулі. Та теорема Ляпунова складають закон великих чисел.
- •Вибірка з генеральної сукупності. Розподіл вибірки. Вибіркові характеристики. Загальні поняття математичної статистики.
- •Надійний інтервал для математичного сподівання ознаки γ нормальним законом розподілу і відомим середньоквадратичним відхиленням.
- •Приклад.
- •Інтервал надійності для оцінки математичного сподівання з нормальним розподілом випадкової величини та не відомим значенням σ.
- •Довірчий інтервал, інтервал надійності оцінки середньоквадратичного відхилення з нормальним законом розподілу.
- •В) .Поняття про умовні варіанти. Метод добутків для знаходження вибіркових середніх і дисперсії.
- •Дисперсія вибірки , де
- •Складаємо наступну розрахункову таблицю
- •Г)Багатовимірні випадкові величини.
- •Розділ 5. Елементи теорії кореляції. А. Функціональна та статистична залежності.
- •Б) Знаходження кореляційного зв‘язку між випадковими величинами у вигляді рівняння лінії регресії.
- •В. Додавання дисперсій
- •Перевірка статистичних гіпотез.
Б) Локальна теорема Лапласа (без доведення)
Зрозуміло, що при великому числі спроб біноміальна функція розподілу обчислюється досить складно,через необхідність обчислення факторіалів великих чисел. Тому часто використовують для обчислення ймовірностей наближені формули. Спробуємо знайти можливість обчислювати ймовірності незалежних спроб, якщо їх число велике.
У
1730 р. Муавр для випадку коли
 ,
а Лаплас узагальнив на довільні
,
а Лаплас узагальнив на довільні довели наступну теорему (теорема
Муавра – Лапласа):
довели наступну теорему (теорема
Муавра – Лапласа):
Нехай
в кожному з «п»
незалежних випробувань ймовірність
настання події А
однакова і рівна p
де (
),
тоді
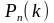 - ймовірність того, що в «п»
спробах подія А
настане «к»
раз визначається виразом:
- ймовірність того, що в «п»
спробах подія А
настане «к»
раз визначається виразом:
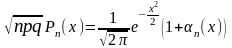
Де:

 для усіх «х»
які знаходяться на певному скінченному
проміжку, рівномірно. Доведення
проводиться з використанням для
обчислення факторіалів формули Стірлінга
для усіх «х»
які знаходяться на певному скінченному
проміжку, рівномірно. Доведення
проводиться з використанням для
обчислення факторіалів формули Стірлінга
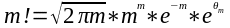
Де
параметр
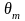 задовольняє нерівності
задовольняє нерівності
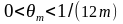 ,
тобто є числом з заданого інтервалу.
,
тобто є числом з заданого інтервалу.
Якщо замість усіх факторіалів в біномному розподілі підставити формулу Стірлінга то отримаємо розподіл Муавра-Лапласа. Слід відмітити, що коли або р або q близькі до нуля то ймовірність можна обчислити або з допомогою формули Муавра-Лапласа, або з допомогою формули Пуассона.
В) Інтегральна теорема Лапласа та її застосування. Функція Лапласа
Часто,
при оцінці рівня сигналу, прийнятого
системою зв'язку, необхідно знати
ймовірність його попадання в заданий
інтервал. Тобто обчислити ймовірність
того, що випадкова подія в п
спробах появиться не менше
 раз і не більше
раз і не більше
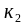 раз. Тобто, обчислити ймовірність
раз. Тобто, обчислити ймовірність
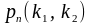 .
Ця ймовірність обчислюється за допомогою
інтегральної
теореми Лапласа.
.
Ця ймовірність обчислюється за допомогою
інтегральної
теореми Лапласа.
Теорема: якщо ймовірність р появи події А в довільній спробі постійна з інтервалу , то ймовірність того, що випадкова подія А в n спробах появиться не менше раз і не більше раз вичислюється з допомогою інтегралу

де,
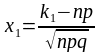 ,
,
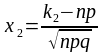 .
.
Зрозуміло, що даний інтеграл аналітично не вичислюється, але може бути обчислений за допомогою функції Лапласа
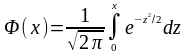 ,
,
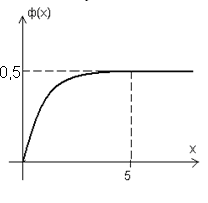
Дана функція табульована, і має наступні властивості:
1.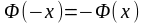 ,
,
2.
В таблицях, як правило, приводяться
значення даної функції лише на інтервалі
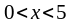 ,
оскільки при
,
оскільки при
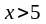
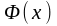
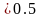 .
Характерний графік залежності
.
Характерний графік залежності
 приведено
на малюнку
приведено
на малюнку
Тоді:
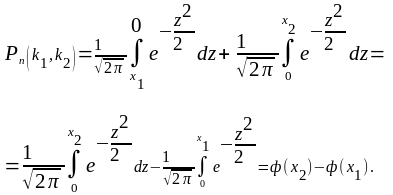
Отже, інтегральну теорему Лапласа можна записати так:
де,
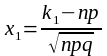 ;
;
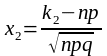 ,
m
– змінна
випадкова величина з інтервалу
,
m
– змінна
випадкова величина з інтервалу
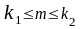
Г) Ймовірність відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях
Нехай
виконується п
незалежних дослідів, в кожному із яких
ймовірність появи події А
однакова і рівна р
Поставимо
задачу знайти ймовірність того, що
відхилення відносної частоти
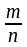 від постійної ймовірності р
по
абсолютній величині не перевищить малу
величину
від постійної ймовірності р
по
абсолютній величині не перевищить малу
величину
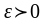 .
Іншими словами знайдемо ймовірність
виконання висловлювання:
.
Іншими словами знайдемо ймовірність
виконання висловлювання:

Цю
ймовірність запишемо як .
Вираз (1) перепишемо наступним чином
.
Вираз (1) перепишемо наступним чином
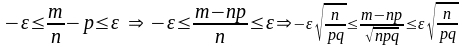
Тоді, шукану ймовірність можна записати у виді

Для обчислення ймовірності застосуємо інтегральну теорему Лапласа, ввівши попередньо позначення
 ,
,
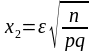
Тоді
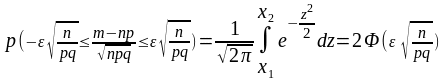 ;
;
Здійснивши зворотне позначення отримаємо
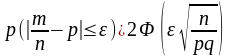 .
.
Отриманий вираз і є оцінкою відхилення відносної частоти від постійної ймовірності.
Приклад.
Нехай ймовірність не стандартної деталі
в партії
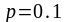 .
Знайти ймовірність того, що серед 400
випадково відібраних деталей відносна
частота появи нестандартної деталі
відрізняється від 0.1 на величину, не
більшу за 0,03.
.
Знайти ймовірність того, що серед 400
випадково відібраних деталей відносна
частота появи нестандартної деталі
відрізняється від 0.1 на величину, не
більшу за 0,03.
Розв'язок. Обчислимо
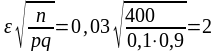 .
.
Тоді шукана ймовірність відхилення відносної частоти від 0.1 становитиме