
- •Конспект лекцій з курсу « Теорія ймовірності та випадкові процеси» Розділ 1 Вступ. Поняття ймовірності.
- •Коротка історична довідка.
- •Непарні
- •Властивості ймовірності подій
- •2. Основні формули комбінаторики.
- •Статистичне визначення ймовірності подій
- •1. Для лінійного випадку
- •2. Для плоского випадку
- •1.Умовна ймовірність.
- •Л) незалежні події. Теорема множення незалежних подій.
- •Часто ймовірність події ā позначають
- •0) Наслідки із додавання і множення.
- •1)Теорема додавання ймовірностей сумісних подій.
- •Р(в) – ймовірність попадання другого.
- •Розділ 2: послідовності незалежних випробовувань. Формула бернуллі
- •Вивід формули Бернуллі:
- •Б) Локальна теорема Лапласа (без доведення)
- •Розділ 3. Основні поняття математичної статистики. Випадкові величини та їх числові характеристики. А. Поняття випадкової величини. Дискретні та неперервні випадкові величини.
- •В. Приклади: біноміальний закон розподілу. Закон розподілу Пуассона.
- •1) Біноміальний закон.
- •2) Розподіл Пуассона.
- •Г. Інтегральна та диференціальна функції розподілу випадкової величини, їх властивості та функція розподілу (крива розподілу).
- •Математичне сподівання та дисперсія випадкових величин.
- •Математичне сподівання має властивості:
- •Властивості дисперсії.
- •Сталий множник можна виключити
- •Якщо ξ: η- незалежні випадкові величини, то
- •Моменти к-того порядку.
- •Є. Ймовірність попадання випадкової величини в заданий інтервал. Нормальний закон розподілу неперервної випадкової величини
- •Правило трьох „σ”.
- •Ж. Поняття про функції випадкового аргументу і її закон розподілу.
- •Дискретна випадкова величина.
- •Неперервні випадкові величини
- •З. Закон великих чисел. Нерівність Чебишева , теореми Чебишева та Бернулі. Поняття про теорему Ляпунова.
- •Теорема Бернулі.
- •Теорема Ляпунова. (Поняття).
- •Теореми Чебишева, Бернулі. Та теорема Ляпунова складають закон великих чисел.
- •Вибірка з генеральної сукупності. Розподіл вибірки. Вибіркові характеристики. Загальні поняття математичної статистики.
- •Надійний інтервал для математичного сподівання ознаки γ нормальним законом розподілу і відомим середньоквадратичним відхиленням.
- •Приклад.
- •Інтервал надійності для оцінки математичного сподівання з нормальним розподілом випадкової величини та не відомим значенням σ.
- •Довірчий інтервал, інтервал надійності оцінки середньоквадратичного відхилення з нормальним законом розподілу.
- •В) .Поняття про умовні варіанти. Метод добутків для знаходження вибіркових середніх і дисперсії.
- •Дисперсія вибірки , де
- •Складаємо наступну розрахункову таблицю
- •Г)Багатовимірні випадкові величини.
- •Розділ 5. Елементи теорії кореляції. А. Функціональна та статистична залежності.
- •Б) Знаходження кореляційного зв‘язку між випадковими величинами у вигляді рівняння лінії регресії.
- •В. Додавання дисперсій
- •Перевірка статистичних гіпотез.
В. Додавання дисперсій
Теорема. Якщо деяка сукупність визначених величин розбита (повністю) на групи, то загальна дисперсія рівна сумі внутрігрупової та між групової дисперсій
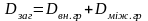
Нехай у нас є дві групи
група 1 група 2
значення
признаку 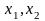
Частоти
появи


Об’єм,
потужність
групи


Групове середнє
значення


Групова
дисперсія

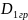
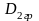
Повний
об’єм всіх випадкових величин

Тоді :
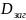

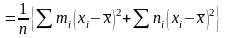
Розглянемо
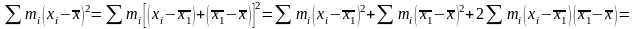

бо

Аналогічно для другого виразу
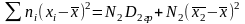
Тоді


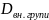



Міра кореляційного зв’язку.
Зрозуміло,
що
при функціональній залежності зв'язок
між X та Y дуже тісний. Адже дисперсія

 для заданого Х.
для заданого Х.
В принципі, при не тісному зв’язку кожному “Х” відповідає ціла сукупність множин значень Y.
Для функціонального зв’язку Для кореляційного зв’язку
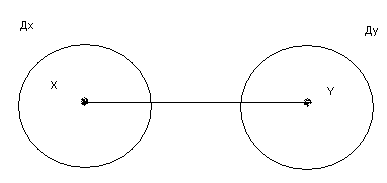
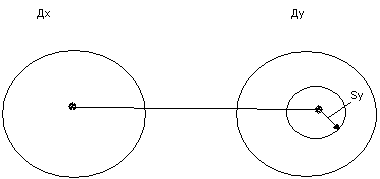
Зв'язок
тісний
 Зв'язок
не тісний
Зв'язок
не тісний

Як же можна оцінити тісноту довільного кореляційного зв’язку?
Нехай результати дослідів приведено в кореляційну таблицю:
-
Y
X
3
9
3
4
13
5
6
7

10
20
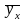
4.2
3.7
Ми маємо дві групи, що відповідають різним значенням Х=3 та Х=9.
В 1 групі 4 рази мали Y=9 та 6 разів Y=5
В 2 групі при (Х=9) мали 13 раз Y=3 та 7 раз Y=5
Можна обчислити умовні групові середні


Оскільки усі значення признаку Y розбито на групи, то загальну дисперсію признака можна представити у вигляді суми внутрігрупової та між групової дисперсій.
Покажемо справедливість таких тверджень:
1)Якщо
зв'язок між X та Y функціональний, то:
2)Якщо
зв'язок кореляційний, то:

Дов. 1 Якщо зв’язок між Х та Y функціональний, то кожному Х відповідає певне значення Y. Тому група виразиться в одне число по Y. Тому групова дисперсія буде рівна 0 і твердження доведене, бо

 ,
звідки очевидно, що
.
,
звідки очевидно, що
.
Дов.
2 Якщо

 при наявності кореляційного зв’язку,
то
, а отже відношення
.
при наявності кореляційного зв’язку,
то
, а отже відношення
.
Ясно,
що таке відношення дисперсій
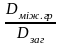
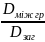 як і власне
як і власне

 може служити мірою
щільності кореляційного зв’язку.
може служити мірою
щільності кореляційного зв’язку.
Переваги та недоліки введення кореляційного зв’язку.
Переваги:
Ясно,
що коли
 зв’язку між Х таY немає зовсім. Якщо ж
зв’язку між Х таY немає зовсім. Якщо ж
 то зв'язок функціональний.
то зв'язок функціональний.
Тому
зростання щільності, зменшення радіуса
кільця біля значення
 ,
супроводжує наближення кореляційного
зв‘язку між випадковими змінними до
функціонального.
,
супроводжує наближення кореляційного
зв‘язку між випадковими змінними до
функціонального.
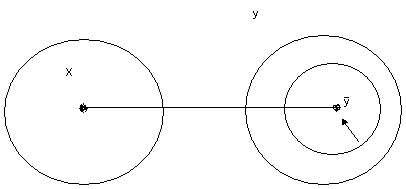
Відмітимо, що даний параметр характеризує довільний функціональний зв'язок, не обов’язково лінійний.
Недоліки:
Недолік полягає в тому, що даний параметр зовсім не вказує який саме функціональний зв'язок є між Х та Y в дійсності, тобто чи є пряма лінія, чи парабола, чи інша функція.
Найпростіші випадки криволінійної кореляції.
Зрозуміло, що зв'язок між Х таY не завжди лінійний. Як це встановити вид функціонального зв’язку?
Краще всього провести, якщо це можливо, теоретичні дослідження опираючись на ряд аксіом та законів фізики, і встановити вид функціональної залежності. При цьому, зрозуміло, випливає ряд параметрів, які встановлюються по експериментальних даних за допомогою методу найменших квадратів.
Так, якщо у нас наявна параболічна залежність (кореляційна) Y від X
Тобто

Де А, В, С, - невідомі постійні, то, користуючись методом найменших квадратів легко отримати сукупність рівнянь.

Розв’язки яких дають шукані значення параметрів А, В, С, і дають опис кореляційного зв’язку.
