Розділ 5. Елементи теорії кореляції. А. Функціональна та статистична залежності.

Оскільки випадкова подія то з‘являється в даних умовах, то вона відсутня, то дуже важко однозначно встановити зв‘язок між заданою однією або декількома умова і власне подією. У цьому розділі будуть розглядатися методи, що дозволяють це зробити.

Функціональний зв‘язок між X та Y існує тоді, коли можна вказати закон або правило згідно якого кожному значенню “ X” із області визначення функції існує одне або кілька значень із області значень функції Y.

Строга функціональна залежність реалізується рідко, так як обидві змінні величини, або одна з них, залежить від дії випадкових неконтрольованих факторів, причому ці фактори можуть впливати як на Y так і на X.

В останньому випадку виникає статистична залежність.

Наприклад, якщо Y залежить від випадкових факторів Z1,Z2,U1,U2, а відповідна X залежить від Z1,Z2, V1,V2 то між X і Y існує статистична залежність.

Статистичною називають залежність, при який зміна однієї із величини приводить до зміни розподілу іншої.

Якщо при зміні однієї із величин змінюється середнє значення іншої то в цьому випадку статистичну залежність називають кореляційною.

Наприклад. Нехай змінною X назвемо кількість внесених добрив ( в рамках розумної міри ) а Y – урожай зерна.

З однакових по розміру ділянок землі при внесенні рівних кількостей добрив знімають різну кількість зерна. Тобто такий зв‘язок є завідомо не функціональним. Однак якщо розглянути середній врожай то, як показує дослід, то він залежить від кількості внесених добрив. Тобто X та Y зв‘язані кореляційно.

Б) Знаходження кореляційного зв‘язку між випадковими величинами у вигляді рівняння лінії регресії.

Розглянемо двомірну величину (X і Y), де X і Y – залежні випадкові величини. Представимо одну із них як функцію іншої. Оскільки точний зв‘язок між ними встановити неможливо, то, наближено, опишемо Y як лінійну функцію X.

Y ≈ g(X) = + x

Зрозуміло, що , - параметри, які підлягають визначенню. Визначити дані величини ( , ) можна різними способами, але найбільш вживаним є метод найменших квадратів.

Функцію називається найкращим наближенням Y в розумінні методу найменших квадратів, якщо математичне сподівання приймає найменше значення.

Отриману функцію називають середньо квадратичною регресією У на "Х".

Теорема. Лінійна середньоквадратична регресія У на Х має вид

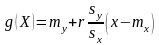
де ; ;

;

- коефіцієнт кореляції величин X та Y, величина - називається коефіцієнтом регресії Yна X, .

Доведення. Нехай є дві випадкові величини X, Y які зв‘язані між собою, і цей зв‘язок необхідно визначити.

У результаті “n” випробувань було отримано “n” впорядкованих пар ; …. .

По даним випадковим значеннях вибірки можна встановити

; а також та а отже і та 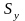. Ми уже говорили, що якщо випадкові величини X та Y незалежні то . Якщо ж вони зв'язані, хоча б якось, то дана рівність не виконується і власне різниця буде в якісь мірі, характеризувати рівень зв‘язку.

Згідно з означенням коефіцієнта кореляції

,

він безрозмірний, і це є основною причиною появи і в знаменнику.

Розглянемо двомірну функцію

Ясно, що

- вказує зв‘язок. - вказує вірно розмірність. Тобто

Тоді

Дослідимо функцію 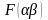на екстремум. Для цього обчислимо перші похідні по параметрах та прирівняємо їх до 0.

.

Тому

Отже

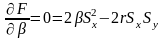
Звідси оптимальні значення параметрів ; .

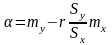При цих значеннях функція має найменше значення.

Тоді

- це рівняння прямої середньоквадратичної регресії Y на X. Якщо підставити отримані та у отримаємо мінімальне, залишкове значення функції:

Величину називають залишковою дисперсією випадкової величини Y відносно випадкової величини Х, вона вказує на величину помилки, що виникає при розрахунку Y як функцію .

При r = ±1; F(x, y)=0.

Іншими словами, якщо то при цих, крайніх значеннях коефіцієнта кореляції не виникає помилки, тобто зв'язок між Y та X є функціональним причому "Y" є лінійною функцією Х.

Аналогічно можна отримати пряму середньоквадратичної регресії X на Y у вигляді:

Залишкова дисперсія величини Х відносно Y.

Як бачимо, при обидві прямі співпадають.

Зауваження 1. Рівняння прямих регресії доцільно знаходити лише в тому випадку, коли впорядковані пари розміщаються поблизу прямої лінії.

Зауваження 2. Якщо число випробувань “n” (об’єм вибірки) дуже великий, то, для спрощення розрахунків, дані можна згрупувати і використати метод умовних варіант.

Вважаємо, що дані уже згруповані і що пари чисел спостерігались раз.

Тоді ці дані записують у формі кореляційної таблиці

У цій таблиці ; ; .

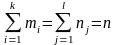n –кількість усіх спостережень.

Тоді формула для розрахунку коефіцієнту кореляції набуде вигляду

Нехай крок розбиття даних по Х буде . Тобто для довільних “i” (варіаційний ряд будується до побудови таблиці).

Нехай крок розбиття даних по Y буде , тобто

Тоді

Де за та - вибираємо номери варіанту що знаходяться приблизно посередині варіаційних рядів по Х та Y відповідно.

Тоді:

Де

; ;

;

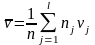Визначений коефіцієнт кореляції, сумісно з відповідними середніми значеннями , та середньоквадратичних значень та , задають рівняння кореляції.

Приклад розрахунку коефіцієнта кореляції, коефіцієнта регресії.

Дані про кількість внесених добрив «Х» і врожайність «У» на 100 га орної землі задамо у таблиці

Х/ У	10	12	14	16	18	20
10	9	4	1
30	1	10	9	3
50		2	6	14	6
70			1	10	18	6

Необхідно знайти рівняння прямих регресії Y на X та X на Y.

Як бачимо обидві змінні і X і Y складають варіаційні ряди. Крок по Y рівний 2, крок по Х буде 20.

1. Складемо кореляційну таблицю в умовних варіантах взявши за умовні нулі

		1	2	3	4	5	6	7
	x\y	-3	-2	-1	0	1	2
1	-2	9	4	1				14
2	-1	1	10	9	3			23
3	0		2	6	14	6		28
4	1			1	10	18	6	35
5		10	16	17	27	24	6	100

Обчислимо і :

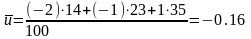
Обчислимо допоміжні величини та :

Обчислимо і :

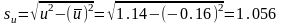
Обчислимо добуток:

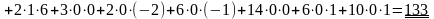
Розраховуємо:

Тоді:

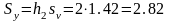
Отже шукане рівняння прямої регресії Y на X буде

або симетризоване

Остаточно:

Аналогічно знаходимо рівняння прямої регресії X на Y:

Значення r однакове в обох рівняннях! Або ж після обчислень .

Слід відмітити, що в останньому виразі під «х» слід розуміти його середнє значення при зміні «y», точно так же і у виразі рівняння прямої регресії Y на X під «у» слід розуміти його середнє значення при зміні «x». Саме тому, внаслідок здійснення тотожних перетворень, рівняння регресії не переходять одне в інше.