
- •Матрицы
- •Направленные отрезки
- •Определение множества векторов
- •1. Коммутативности
- •2. Ассоциативности
- •3. Дистрибутивности
- •Линейная зависимость векторов
- •Базис. Координаты вектора в базисе
- •Действия с векторами в координатном представлении
- •(Сравнение векторов). Два вектора
- •(Сложение векторов). Координатное представление суммы двух векторов
- •(Умножение векторов на число). Координатное представление произведения вектора
- •Декартова система координат
- •1.8 Изменение координат при замене базиса и смещения начала координат
- •Ортогональные проекции
- •2.2. Скалярное произведение векторов и его свойства
- •2.3. Выражение скалярного произведения в координатах
- •2.4. Векторное произведение векторов и его свойства
- •2.5. Выражение векторного произведения в координатах
- •2.6. Смешанное произведение
- •2.7. Выражение смешанного произведения в координатах
- •2.8. Двойное векторное произведение
2.4. Векторное произведение векторов и его свойства
Определение
2.5. Упорядоченная
тройка некомпланарных
векторов
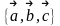 называется правой,
если (после
совмещения их начал) кратчайший поворот
от вектора
к вектору
называется правой,
если (после
совмещения их начал) кратчайший поворот
от вектора
к вектору
 виден из конца вектора
виден из конца вектора
 совершающимся против часовой стрелки.
В противном случае упорядоченная тройка
некомпланарных векторов
называется левой.
совершающимся против часовой стрелки.
В противном случае упорядоченная тройка
некомпланарных векторов
называется левой.
Определение
2.6. Векторным
произведением
неколлинеарных векторов
и
называется вектор
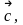 такой, что
такой, что
1.
 ,
где
–
угол
между
векторами
и
,
где
–
угол
между
векторами
и
2. Вектор ортогонален вектору и вектору .
3. Тройка векторов правая.
В случае, когда сомножители коллинеарны (в том числе, когда хотя бы один из сомножителей есть нулевой вектор), векторное произведение считается равным нулевому вектору.
Векторное
произведение векторов
и
обозначается как
 .
Из определения 2.6 следует, что
.
Из определения 2.6 следует, что
1.
 есть площадь параллелограмма, построенного
на векторах
и
.
есть площадь параллелограмма, построенного
на векторах
и
.
2. Для коллинеарности ненулевых векторов и необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.
Свойства векторного произведения
1.  (антикоммутативность, следует из
определения 2.6 и нечетности функции
(антикоммутативность, следует из
определения 2.6 и нечетности функции
 ).
).
2. 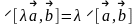 (следует из определения векторного
произведения и того факта, что векторы
(следует из определения векторного
произведения и того факта, что векторы
 и
и
 ортогональны одной и той же плоскости
при неколлинеарных
и
и
ортогональны одной и той же плоскости
при неколлинеарных
и
и
 ).
).
3.  (дистрибутивность).
(дистрибутивность).
2.5. Выражение векторного произведения в координатах
Пусть задан правый базис , то есть, такой, что векторы образуют правую тройку, и два вектора и , координатные разложения которых в этом базисе имеют вид
и .
По свойствам 2 и 3 векторного произведения

Обозначим
через
 и
и
 попарные векторные произведения базисных
векторов
попарные векторные произведения базисных
векторов
 следующим образом:
следующим образом:

Подставив
эти обозначения в выражение для
 и использовав формулу, связывающую
определители квадратных матриц 2-го и
3-го порядков (см. теорему 1.1), получим
и использовав формулу, связывающую
определители квадратных матриц 2-го и
3-го порядков (см. теорему 1.1), получим

Случай ортонормированного базиса
Пусть
исходный базис
 ортонормированный,
образующий правую
тройку
векторов, тогда по определению 2.6,
ортонормированный,
образующий правую
тройку
векторов, тогда по определению 2.6,
 .
.
Тогда формула для векторного произведения векторов в ортонормированном базисе упростится:

Из вышеприведенных формул вытекают полезные следствия.
Следствие 1. Для того чтобы векторы и были коллинеарные, необходимо и достаточно, чтобы в любом базисе
 ,
,
или же
 .
.
Следствие
2. В ортонормированном базисе площадь
параллелограмма, построенного на
векторах
и
 вычисляется по формуле
вычисляется по формуле
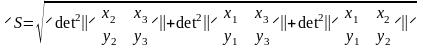 ,
,
причем для случая базиса на плоскости
 .
.
2.6. Смешанное произведение
Определение
2.7 Смешанным
произведением векторов
,
и
обозначаемым как
 ,
называется число
,
называется число
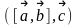 .
.
Теорема 2.1 Абсолютная величина смешанного произведения векторов равна объему параллелепипеда, построенного на векторах , и . При этом если тройка векторов , , некомпланарная и правая, то их смешанное произведение положительно, а если тройка левая, то – отрицательно.
Доказательство.
Если
коллинеарен
 то утверждение теоремы очевидно. Пусть
неколлинеарен
тогда по определению скалярного
произведения
то утверждение теоремы очевидно. Пусть
неколлинеарен
тогда по определению скалярного
произведения
 ,
,
Р Теорема доказана. |
где
S
=
| [
– высота параллелепипеда с основанием S, откуда (см. рис. 2.6.1)
Наконец,
что и позволяет сделать заключение о знаке смешанного произведения. |
Свойства смешанного произведения
Для смешанного произведения справедливы тождества:
1.

 ;
;
2.
 ;
;
3.
 ,
,
справедливость которых следует из определения смешанного произведения и теоремы 2.1.
Отметим, что смешанное произведение равно нулю, если среди сомножителей имеется хотя бы одна пара коллинеарных векторов.


 ис.
2.3
ис.
2.3 ]
| есть площадь параллелограмма,
построенного на векторах
и
,
а
]
| есть площадь параллелограмма,
построенного на векторах
и
,
а
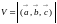 .
.