Ортогональные проекции
Определение 2.1. Прямая l с расположенным на ней ненулевым вектором называется осью. Вектор называется направляющим вектором оси l.
M
l M*
Рис. 2.1 |
Прямую l, с расположенным на ней ненулевым вектором будем называть осью. Вектор называется направляющим вектором оси l. Пусть дана точка M, не лежащая на оси l, тогда основание перпендикуляра, опущенного из M на ось l – точку M*, будем называть ортогональной проекцией точки M на ось. |
Определение
2.2. Ортогональной
проекцией вектора
на ось l
называется вектор
лежащий на оси l,
начало которого есть ортогональная
проекция начала
вектора
на ось l,
а конец – ортогональная проекция конца
вектора
Выполним
нормировку направляющего вектора
,
то есть заменим его на вектор
и рассмотрим нормированный базис
на оси l
(рис. 2.1).
Определение 2.3. Углом между ненулевыми векторами и называется величина наименьшего из двух углов, образуемых этими векторами при совмещении их начал.
Численное
значение ортогональной проекции вектора
на ось l
обозначим
.
Из рис. 2.2 видно, что
,
где
есть угол между
и
.
φ
Рис. 2.2
2.2. Скалярное произведение векторов и его свойства
Определение 2.4. Скалярным произведением ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.
В случае, когда хотя бы один из сомножителей есть нулевой вектор, скалярное произведение считается равным нулю.
Скалярное
произведение векторов
и
обозначается как
.
Таким образом, для ненулевых векторов
и
:
где
– угол между векторами-сомножителями.
При этом, согласно определению 2.3,
.
Заметим
также, что, если
,
то справедливо равенство
.
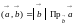Свойства скалярного произведения
1. 
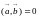при
и
тогда и только тогда, когда
и
взаимно
ортогональны;
2. 
следует из определения скалярного
произведения и свойств косинуса
(коммутативность).
3. 
(дистрибутивность).
4. 
;
5. 
;
(заметим
также, что условия
и
равносильны);
6. При
и
,
где
– угол меду векторами
и
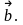
2.3. Выражение скалярного произведения в координатах
Пусть
задан базис
и два вектора
и
координатные разложения которых в этом
базисе имеют вид
и
.
По свойствам 3 и 4 скалярного произведения
В случае ортонормированного базиса эта формула упрощается, поскольку для попарных скалярных произведений базисных векторов справедливо равенство
где
– так называемый символ
Кронекера.
Откуда для скалярного произведения
векторов в ортонормированном базисе
получаем формулу
,
из которой следуют полезные соотношения:
и
для
и
.
Отметим,
что последнее равенство в сочетании с
условием
приводит к неравенству
Коши–Буняковского:
Задача 3. Найти расстояние между двумя точками в ортонормированной системе координат, если известны радиусы-векторы этих точек.
Решение.
Пусть
задана ортонормированная система
координат
и радиусы-векторы точек
и
в ней. Тогда, используя решение задачи 1, из равенства
и свойств скалярного произведения получаем
.