
- •Матрицы
- •Направленные отрезки
- •Определение множества векторов
- •1. Коммутативности
- •2. Ассоциативности
- •3. Дистрибутивности
- •Линейная зависимость векторов
- •Базис. Координаты вектора в базисе
- •Действия с векторами в координатном представлении
- •(Сравнение векторов). Два вектора
- •(Сложение векторов). Координатное представление суммы двух векторов
- •(Умножение векторов на число). Координатное представление произведения вектора
- •Декартова система координат
- •1.8 Изменение координат при замене базиса и смещения начала координат
- •Ортогональные проекции
- •2.2. Скалярное произведение векторов и его свойства
- •2.3. Выражение скалярного произведения в координатах
- •2.4. Векторное произведение векторов и его свойства
- •2.5. Выражение векторного произведения в координатах
- •2.6. Смешанное произведение
- •2.7. Выражение смешанного произведения в координатах
- •2.8. Двойное векторное произведение
Действия с векторами в координатном представлении
Поскольку в конкретном базисе каждый вектор находится во взаимно однозначном соответствии с упорядоченной тройкой чисел – своим координатным представлением, то естественно возникает вопрос о том, как выполняются операции с векторами в координатном представлении.
Оказывается, что возможно не только записывать векторы при помощи матриц (столбцов), но и оперировать с ними в матричной форме, поскольку правила действий с векторами в координатной форме совпадают с правилами соответствующих операций с матрицами.
Теорема 1.9 В координатном представлении операции с векторами выполняются следующим образом:
(Сравнение векторов). Два вектора

равны тогда и только тогда, когда равны их координатные представления:
 или
или
 .
.
(Сложение векторов). Координатное представление суммы двух векторов
равно сумме координатных представлений слагаемых

(Умножение векторов на число). Координатное представление произведения вектора
на число равно произведению координатного представления вектора на это число :

Доказательство.
Поскольку рассуждения для всех трех пунктов аналогично, рассмотрим лишь правило сложения векторов в координатной форме.
По свойствам операций сложения и умножения на вещественное число векторов (теорема 1.3.1) имеем


Теорема доказана
Рассмотрим теперь, как в координатном представлении записываются условия линейной зависимости и независимости векторов.
Теорема
1.10. Для
того чтобы два вектора
и
на плоскости были линейно зависимы,
необходимо и достаточно, чтобы их
координаты
 и
и
 в некотором базисе удовлетворяли условию
в некотором базисе удовлетворяли условию

Доказательство.
Докажем
необходимость.
Пусть векторы
и
линейно зависимы, тогда в силу леммы 1
имеет место равенство
 или в координатной форме
или в координатной форме
 .
Исключив
из этих двух скалярных соотношений,
получим
.
Исключив
из этих двух скалярных соотношений,
получим
 но
это и означает, что
но
это и означает, что

Докажем
достаточность.
Пусть
 тогда имеем, что
тогда имеем, что
 при
при
 ,
то есть соответствующие координаты
векторов
и
пропорциональны, что и доказывает
линейную зависимость этих векторов.
,
то есть соответствующие координаты
векторов
и
пропорциональны, что и доказывает
линейную зависимость этих векторов.
Случай
 предлагается рассмотреть самостоятельно.
предлагается рассмотреть самостоятельно.
Теорема доказана.
Теорема
1.11. Для
того чтобы три вектора
 с координатными представлениями в
некотором базисе
с координатными представлениями в
некотором базисе
 ,
,
 и
и

в пространстве были линейно зависимы, необходимо и достаточно, чтобы их координаты удовлетворяли условию

Доказательство.
Пусть
линейная комбинация векторов
 равна нулевому, то есть
равна нулевому, то есть
 или, в координатном представлении,
или, в координатном представлении,
 .
.
Данное матричное равенство очевидно равносильно системе линейных уравнений

основная матрица которой - согласно теореме Крамера - невырождена тогда и только тогда, когда эта система имеет единственное решение.
Но также очевидно, что эта система всегда имеет нулевое (тривиальное) решение. А значит, условие

равносильно
равенству
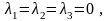 что и доказывает утверждение теоремы.
что и доказывает утверждение теоремы.
Теорема доказана.
Декартова система координат
Определение
1.25.
Совокупность
базиса
 и точки O,
в которую помещены начала всех базисных
векторов, называется общей
декартовой системой координат
и обозначается
и точки O,
в которую помещены начала всех базисных
векторов, называется общей
декартовой системой координат
и обозначается
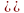
Определение
1.26. Система
координат
 ,
порождаемая ортонормированным базисом,
называется нормальной
прямоугольной
(или ортонормированной)
системой координат.
,
порождаемая ортонормированным базисом,
называется нормальной
прямоугольной
(или ортонормированной)
системой координат.
Если
задана система координат
,
то произвольной точке M
в пространстве можно поставить во
взаимно однозначное соответствие вектор
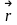 ,
начало которого находится в точке O,
а конец – в точке M.
,
начало которого находится в точке O,
а конец – в точке M.
Определение
1.27. Вектор
 называется радиусом-вектором
точки M
в системе координат
называется радиусом-вектором
точки M
в системе координат
Определение 1.28. Координаты радиуса-вектора точки M называются координатами точки M в системе координат
Особенности использования векторно-координатного описания геометрических объектов рассмотрим на примере решения следующих задач.
Задача
1. В
некоторой общей декартовой системе
координат
заданы координаты радиусов-векторов
точек M
и N,
которые являются началом и концом
вектора
 Требуется найти координаты вектора
Требуется найти координаты вектора
Решение.
N
O
Рис. 1.8 |
Решение очевидно из рис. 1.8 и свойств координат векторов. Пусть
Тогда
имеем
|
Задача
2.
В
некоторой общей декартовой системе
координат
заданы координаты несовпадающих точек
 и
и
 ,
для которых соответственно
,
для которых соответственно
 и
и
 .
.
Требуется
найти точку M,
такую, что

Решение.
Заметим, что
может принимать любое значение, кроме
 ,
при котором точка M
уходит в бесконечность (рис. 1.7.2). Найдем
радиус-вектор точки M.
Из соотношений в треугольниках
,
при котором точка M
уходит в бесконечность (рис. 1.7.2). Найдем
радиус-вектор точки M.
Из соотношений в треугольниках
 и
и
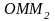 получаем
получаем

M
O
Рис. 1.9 |
но,
так как
и окончательно,
Откуда радиус-вектор точки M равен
|
 в силу теоремы 1.9.
в силу теоремы 1.9.

 M
M и
и
 .
. и
и
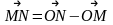 .
Окончательно
.
Окончательно .
.
 то
то
