
- •Матрицы
- •Направленные отрезки
- •Определение множества векторов
- •1. Коммутативности
- •2. Ассоциативности
- •3. Дистрибутивности
- •Линейная зависимость векторов
- •Базис. Координаты вектора в базисе
- •Действия с векторами в координатном представлении
- •(Сравнение векторов). Два вектора
- •(Сложение векторов). Координатное представление суммы двух векторов
- •(Умножение векторов на число). Координатное представление произведения вектора
- •Декартова система координат
- •1.8 Изменение координат при замене базиса и смещения начала координат
- •Ортогональные проекции
- •2.2. Скалярное произведение векторов и его свойства
- •2.3. Выражение скалярного произведения в координатах
- •2.4. Векторное произведение векторов и его свойства
- •2.5. Выражение векторного произведения в координатах
- •2.6. Смешанное произведение
- •2.7. Выражение смешанного произведения в координатах
- •2.8. Двойное векторное произведение
ВЕКТОРЫ
И ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД НИМИ
Лекция 1
Матрицы
Аналитическое описание геометрических фигур можно значительно упростить, используя специальный математический объект – матрица.
Определение
1.1.
Матрицей размера
 называется прямоугольная таблица чисел,
содержащая m
строк
и n
столбцов.
называется прямоугольная таблица чисел,
содержащая m
строк
и n
столбцов.
Числа,
составляющие матрицу, называются ее
элементами или компонентами. Они
характеризуются как своими значениями,
так и номерами строк и столбцов. Будем
обозначать элемент матрицы, расположенный
в
 -й
строке и
-й
строке и
 -м
столбце, как
-м
столбце, как

Определение 1.2. Числа m и n называют размерами матрицы.
Матрицы обозначаются и записываются перечислением их элементов

из
которых чаще будем использовать
последнюю. Если развернутое представление
матрицы не требуется, то будут
использоваться записи
 ,
,
 или
или
 и А.
и А.
Матрицы принято классифицировать по количеству их строк и столбцов.
Определение
1.3.
Если
 ,
то матрица называется квадратной,
порядка
n.
Матрица размера
,
то матрица называется квадратной,
порядка
n.
Матрица размера
 называется m-мерным
столбцом.
Матрица размера
называется m-мерным
столбцом.
Матрица размера
 называется n-мерной
строкой.
называется n-мерной
строкой.
Формально
для обозначения строк или столбцов
следует использовать двухиндексные
записи
 или
или
 ,
однако, неменяющиеся индексы принято
опускать, в результате чего обозначения
строк или столбцов принимают вид
,
однако, неменяющиеся индексы принято
опускать, в результате чего обозначения
строк или столбцов принимают вид
 или соответственно
или соответственно
 .
В этих случаях, разумеется, необходимо
явно указывать, о чем идет речь: о строке
или о столбце.
.
В этих случаях, разумеется, необходимо
явно указывать, о чем идет речь: о строке
или о столбце.
Некоторые матрицы с особыми свойствами элементов имеют особые названия и обозначения.
Определение
1.4.
Квадратная матрица
 ,
для которой
,
для которой
 называется симметричной.
называется симметричной.
Матрица,
все элементы которой равны нулю,
называется нулевой.
Нулевую матрицу будем обозначать
 или О.
или О.
Квадратная матрица порядка n вида

называется
единичной
матрицей.
Единичную матрицу принято обозначать
 или E.
или E.
Операции с матрицами
Определение
1.5. Две
матрицы
и
 называются равными
(обозначается:
называются равными
(обозначается:
 или
или
 ),
если они одинаковых размеров и если их
соответствующие компоненты равны, то
есть
),
если они одинаковых размеров и если их
соответствующие компоненты равны, то
есть
 и
и
 .
.
Определение
1.6. Матрица
 называется суммой
матриц
и
(обозначается:
называется суммой
матриц
и
(обозначается:
 или
или ),
если матрицы
,
,
одинаковых размеров и
),
если матрицы
,
,
одинаковых размеров и
 ,
где числа
,
где числа

 являются соответствующими компонентами
матрицы
.
являются соответствующими компонентами
матрицы
.
Определение
1.7. Матрица
 называется произведением
числа
называется произведением
числа
 на матрицу
на матрицу
 (обозначается:
(обозначается:
 или
или
 ),
если матрицы
и
одинаковых размеров и
),
если матрицы
и
одинаковых размеров и
 .
.
Замечание. Умножать на число можно матрицу любого размера.
Определение 1.8. Транспонированием матрицы называется операция, в результате которой образуется новая матрица, где строками служат столбцы исходной матрицы, записанные с сохранением порядка их следования.
Матрица,
получающаяся в результате транспонирования
матрицы А,
обозначается
 при этом
при этом

то
есть для элементов транспонированной
матрицы
при
 верно равенство:
верно равенство:
 .
.
Операция
транспонирования, например, не изменяет
симметричную матрицу, но переводит
строку размера
 в столбец размера
и наоборот.
в столбец размера
и наоборот.
Детерминанты (определители) квадратных матриц
2-го и 3-го порядка
Для
квадратных матриц существует специальная
числовая характеристика, называемая
детерминантом (или определителем),
которая обозначается как
 или
или .
Изучение свойств определителей квадратных
матриц n-го
порядка будет выполнено позже, здесь
же ограничимся рассмотрением определителей
квадратных матриц 2-го и 3-го порядков.
.
Изучение свойств определителей квадратных
матриц n-го
порядка будет выполнено позже, здесь
же ограничимся рассмотрением определителей
квадратных матриц 2-го и 3-го порядков.
Определение 1.9. Детерминантом (определителем) квадратной матрицы 2-го порядка

называется число

 .
.
Определение 1.10. Детерминантом (определителем) квадратной матрицы 3-го порядка

называется число


Для определителей квадратных матриц справедливы следующие теоремы:
Теорема 1.1. Определитель матрицы 3-го порядка может быть выражен через определители 2-го порядка формулой следующего вида:

называемой разложением определителя по первой строке.
Доказательство.
Данная формула проверяется непосредственно при помощи определений 1.9 и 1.10.
Замечание. Формулы, аналогичные приведенной в формулировке теоремы 1.1, могут быть получены как для каждой из остальных строк матрицы, так и для любого из ее столбцов.

Рис. 1.1.
Замечание. Иногда подсчет значения определителя матрицы 3-го порядка удобнее выполнить по следующему правилу: каждое слагаемое в определении 1.10 есть произведение некоторой тройки элементов матрицы, причем элементы, входящие в произведения, берущиеся со знаком "плюс", соединены на рис. 1.1. сплошными линиями, элементы, входящие в произведения, берущиеся со знаком "минус", - утолщенным пунктиром.
Из определений 1.9 и 1.10 непосредственной проверкой можно получить следствие:
Следствие. При транспонировании квадратных матриц 2-го или 3-го порядка их определители не меняются.
С помощью определителей матриц второго порядка удобно формулируется условие однозначной разрешимости системы двух линейных уравнений с двумя неизвестными.
Теорема 1.2.(Крамера) Для того чтобы система линейных уравнений

имела единственное решение, необходимо и достаточно, чтобы

Доказательство.
Докажем
необходимость.
Пусть данная система линейных уравнений
имеет единственное решение – упорядоченную
пару чисел
 ,
тогда должны быть справедливыми следующие
из ее уравнений соотношения:
,
тогда должны быть справедливыми следующие
из ее уравнений соотношения:

или
 где
где
 ,
а
,
а
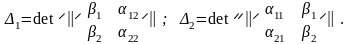
Равенства
 не верны при
не верны при
 или при
или при
 .
.
В
то же время (проверьте это самостоятельно)
при
 коэффициенты уравнений исходной системы
обязаны быть пропорциональными, и тогда
у нее имеется бесчисленное множество
решений – пар чисел
,
таких, что
коэффициенты уравнений исходной системы
обязаны быть пропорциональными, и тогда
у нее имеется бесчисленное множество
решений – пар чисел
,
таких, что
 .
.
Поэтому
из условия существования и единственности
решения следует, что

Докажем
достаточность.
Если
 ,
то исходная система линейных уравнений
имеет решение
,
то исходная система линейных уравнений
имеет решение
 ,
однозначно определяется значениями
параметров
,
однозначно определяется значениями
параметров


 и формулами
и формулами
 и
и
 .
.
Теорема доказана.
Лекция 2
