1.3 Линейная и квадратичная регрессия

Найдем приближающую функцию в виде:

F(x, a, b) = ax + b (11)

Частные производные по параметрам:

∂F/∂а = x; ∂F/∂b = 1 (12)

Составим систему вида (6-8):

∑ (y_i - ax_i - b)x_i = 0; ∑ (y_i - ax_i - b) = 0 (13)

Сумма здесь и далее берется по параметру i в пределах от 1 до n . Далее имеем:

∑ x_i y_i - a∑ x²_i - b∑x_i = 0; ∑ y_i - a∑ x²_i - nb = 0 (14)

или, деля каждое уравнение на n:

(n^-1 ∑ x²_i) · a +(n^-1 ∑x_i) · b = n^-1 ∑ x_i y_i (15)

(n^-1∑x_i) · a + b = n^-1 ∑ y_i (16)

Введем обозначения:

M_x = n^-1∑x_i ; M_y = n^-1 ∑ y_i ; M_xy = n^-1 ∑ x_i y_i ; M_x² = n^-1 ∑ x²_i; (17)

Тогда система будет иметь вид:

M_x²a + M b = M_xy ; M_x a + b = M_y (18)

Коэффициенты этой системы M_x, M_y, M_xy, M_xy, - числа, которые в каждой конкретной задаче приближения могут быть легко вычислены по формулам (17). Решив систему (18), получим значения параметров a и b, а следовательно, и конкретный вид линейной функции (11).

Для квадратичной приближающей функции:

F(x, a, b ,c) = ax² + bx + c (19)

Частные производные:

∂F/∂а = x²; ∂F/∂b = x, ∂F/∂c = 1 (20)

Находим систему вида (6) - (8):

∑ (y_i - ax²_i - bx_i - c)x²_i = 0; ∑ (y_i - ax²_i - bx_i - c)x_i = 0 (21)

∑ (y_i - ax²_i - bx_i - c) = 0 (22)

После несложных преобразований получается система трех линейных уравнений с тремя неизвестными a, b и с. Коэффициенты системы, так же как и в случае линейной функции, выражаются через неизвестные данные из таблицы 1:

M_x⁴ a + M _x³ b + M _x² c = M _x²_y ;

M_x³ a + M _x² b + M _x c = M _xy ; (23)

M_x² a + M _x b + c = M _y ;

Здесь использованы следующие обозначения:

M_x⁴ = n^-1 ∑x⁴_i ; M_x³ = n^-1 ∑x³_i ; M _x²_y = n^-1 ∑x²_iy_i (24)

Решение системы (23) дает значения параметров a, b и с для приближающей функции (19). Примеры нахождения приближающих функций в виде других элементарных функций представлены в работе [2].

2. Задание на расчет

Cоставить алгоритм и программу аналитической аппроксимации функции, заданной таблично. Найти такие значения δ₁ и δ₂, входящие в уравнение (25), при которых погрешность аппроксимации табличной функции с помощью соотношения (25) минимальна. Внести предложения по модификации соотношения (25) с целью снижения величины абсолютной погрешности.

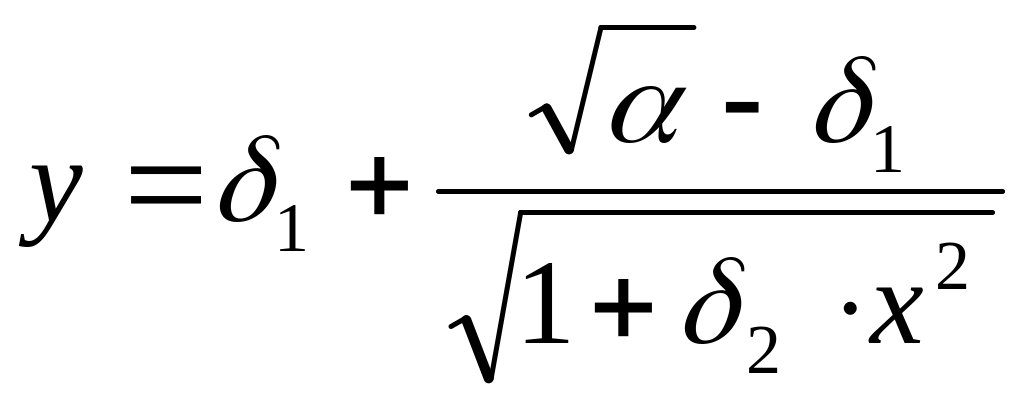(25)

Ниже приведены примеры программ в системе MathCad и MatLab для решения данного задания.

Варианты заданий:

Таблица 2

α = 4

№	Y = 1	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
1	1.212	0.896	0.637	0.477	0.373	0.296	0.234	0.181	0.132	0.082
2	1.679	1.438	1.187	0.944	0.746	0.592	0.468	0.361	0.263	0.163
3	2.014	1.809	1.589	1.347	1.105	0.887	0.702	0.542	0.394	0.245
4	2.274	2.096	1.896	1.67	1.423	1.171	0.935	0.722	0.525	0.327
5	2.501	2.329	2.143	1.931	1.692	1.431	1.161	0.902	0.656	0.408
6	2.636	2.522	2.347	2.146	1.916	1.657	1.374	1.079	0.787	0.49
7	2.828	2.684	2.517	2.325	2.104	1.852	1.656	1.249	0.918	0.571
8	2.927	2.821	2.66	2.475	2.262	2.016	1.733	1.407	1.046	0.653
9	3.076	2.937	2.781	2.601	2.394	2.156	1.877	1.55	1.17	0.734
10	3.166	3.035	2.882	2.706	2.505	2.272	1.999	1.675	1.286	0.815

Таблица 3

α = 9

№	Y =1	1.15	1.3	1.45	1.6	1.75	1.9	2.05	2.2	2.35	2.5
11	1.851	1.671	1.358	1.079	0.872	0.719	0.6	0.503	0.419	0.345	0.276
12	2.682	2.507	2.26	1.984	1.698	1.43	1.199	1.005	0.837	0.689	0.552
13	3.175	3.091	2.88	2.637	2.364	2.072	1.779	1.503	1.256	1.033	0.828
14	3.543	3.545	3.355	3.135	2.884	2.602	2.297	1.979	1.669	1.376	1.104
15	4.201	3.916	3.74	3.536	3.301	3.034	2.736	2.408	2.063	1.716	1.379
16	4.254	4.225	4.059	3.866	3.644	3.391	3.103	2.779	2.423	2.042	1.652
17	4.482	4.486	4.327	4.142	3.93	3.688	3.41	3.095	2.739	2.344	1.917
18	4.895	4.706	4.553	4.375	4.171	3.937	3.669	3.363	3.013	2.615	2.167
19	5.068	4.892	4.743	4.571	4.373	4.146	3.886	3.588	3.246	2.852	2.396
20	5.273	5.049	4.903	4.735	4.542	4.32	4.067	3.777	3.443	3.055	2.6

Таблица 4

α = 16

№	1.1	1.3	1.5	1.7	1.9	2.1	2.3	2.5	2.7	2.9	3.1
21	2.544	2.232	1.885	1.553	1.284	1.076	0.912	0.775	0.659	0.556	0.463
22	3.623	3.392	3.117	2.802	2.463	2.126	1.818	1.549	1.317	1.111	0.924
23	4.394	4.197	3.962	3.687	3.374	3.029	2.666	2.307	1.972	1.666	1.386
24	5	4.823	4.611	4.363	4.076	3.751	3.39	3	2.604	2.215	1.847
25	5.497	5.333	5.136	4.906	4.639	4.334	3.988	3.602	3.183	2.744	2.303
26	5.913	5.757	5.572	5.355	5.103	4.813	4.482	4.108	3.69	3.231	2.743
27	6.264	6.116	5.938	5.731	5.49	5.212	4.895	4.534	4.124	3.663	3.154
28	6.562	6.418	6.247	6.047	5.815	5.548	5.242	4.892	4.493	4.039	3.523
29	6.814	6.674	6.508	6.314	6.088	5.829	5.532	5.193	4.805	4.359	3.847
30	7.025	6.889	6.727	6.537	6.317	6.065	5.775	5.445	5.066	4.63	4.126

3. ПРИМЕР ПРОГРАММНОЙ РЕАЛИЗАЦИИ

3.1. Программа поиска эмпирических коэффициентов по МНК в системе MathCad:

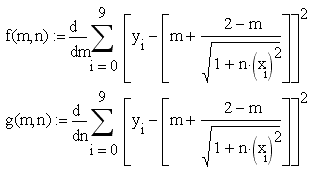
4. СОДЕРЖАНИЕ ОТЧЕТА

4.1 Наименование и цель работы.

4.2 Теоретическая часть.

4.3 Задание на расчет.

4.4 Результаты расчета и выводы.

4.5 Источники информации.

Литература

1. Алексеев А.П. Информатика 2003 / А.П. Алексеев. М.: Солон-Пресс, 2003. 464 с.

2. Заварыкин В.М. Численные методы / В.М. Заварыкин, В.Г. Житомирский, М.П. Лапчик. М.: Просвещение, 1991. 176 с.

ОБРАБОТКА ЧИСЛОВЫХ ДАННЫХ

Методическое указание

к лабораторной работе

Составил КОМАРОВ Вячеслав Вячеславович

Рецензент А.А. Димитрюк

Корректор Д.А.Козлова

Подписано в печать Формат 60х84 ^1/16

Бум. тип. Усл. печ. л. Уч. – изд. л.