4.2.4. Властивості ланцюгів Маркова.

Відзначимо тепер деякі властивості марковських ланцюгів, які стосуватимуться лише ергодичних та поглинаючих скінченних ланцюгів Маркова. Доведення сформульованих нижче тверджень опускаємо (їх можна знайти, наприклад, в [4], а також в додатковій літературі, яка наведена в кінці даного розділу).

Ергодична властивість. За деяких умов у ланцюгу Маркова із зростанням (номера кроку) встановлюється стаціонарний режим, в якому система продовжує блукати по станах, проте ймовірності цих станів вже не залежать ні від номера кроку, ні від початкового розподілу ймовірностей. Такі ймовірності називаються граничними (або фінальними) ланцюга Маркова. Надалі фінальні ймовірності позначатимемо через , а вектор , координатами яких є граничні ймовірності будемо називати граничним (або фінальним) вектором.

Наступна теорема описує широкий клас марковських ланцюгів, які володіють наступною властивістю: граничні ймовірності , , не тільки існують, утворюють розподіл ймовірностей , але і такі, що для всіх і (такі розподіли називаються ергодичними).

Теорема (ергодична теорема). Нехай – матриця перехідних ймовірностей ланцюга Маркова зі скінченною множиною станів . Тоді, якщо ланцюг Маркова ергодичний, то існують числа такі, що

(4.69)

i для будь-якого

(4.70)

Навпаки, якщо існують числа , що задовольняють умови (4.69), (4.70), то ланцюг Маркова ергодичний.

Числа є єдиним розв’язком системи рівнянь

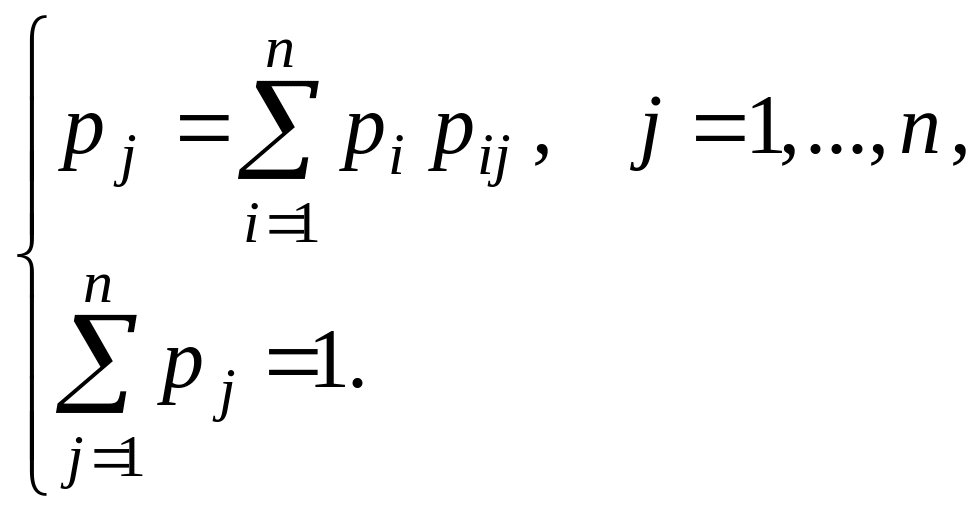(4.71)

Система рівнянь (4.71) відіграє важливу роль в теорії ланцюгів Маркова. Кожний її невід’ємний розв’язок прийнято називати стаціонарним або інваріантним розподілом ймовірностей для марковського ланцюга з матрицею перехідних ймовірностей . Пояснення цієї назви полягає в наступному.

Візьмемо розподіл в якості початкового, Тоді

і взагалі . Іншими словами, якщо в якості початкового розподілу взяти , то цей розподіл не буде змінюватися зі зміною числа кроків (з часом), тобто для будь-якого

Відзначимо, що стаціонарний розподіл ймовірностей ( і до того ж єдиний) може існувати і для неергодичних ланцюгів. Справді (див. приклад 4.10), якщо

,

то

і, отже, границі не існують. У той же час система рівнянь (4.71) перетворюється в систему

,

єдиним розв’язком якої є

Приклад 4.11. Поведінка ринку цінних паперів виявляє наступну тенденцію: операції, в яких ціни зростають, змінюються операціями, в яких ціни падають. Спостереження показали, що умовна ймовірність зростання цін після попереднього періоду їх падіння дорівнює 0,65, а умовна ймовірність спадання цін після попереднього періоду їх зростання дорівнює 0,6.

Визначити відповідні стани, побудувати їх розмічений граф, виписати матрицю перехідних ймовірностей і знайти граничні ймовірності станів.

Розв’язання. В якості системи будемо розглядати ринок цінних паперів. Тоді система може знаходитися лише в двох станах: – падіння цін, і – зростання цін, а отже, процес, що відбувається в системі є дискретним.

Майбутній стан, в який перейде система , залежить (істотно) від стану, в якому вона знаходиться в даний момент часу, тому цей процес є марковським.

Будемо припускати, що моменти часу настільки близькі один до одного, що між ними система не змінює свого стану і, як наслідок, процес, який відбувається в системі , з певною похибкою можна вважати процесом з дискретним часом.

Умовні ймовірності 0,65 і 0,6, що задані в умові прикладу, є очевидно ймовірностями і .

Тоді, використовуючи нормуючу умову (4.52), при для одержимо: ; .

Розмічений граф станів системи матиме наступний вигляд (див. рис. 4.8):

Матриця перехідних ймовірностей

. (4.72)

Оскільки всі елементи матриці додатні, то ланцюг Маркова ергодичний і тому існують граничні ймовірності та відповідно станів та . Із системи рівнянь (4.71) при з матрицею , яка визначається формулою (4.72), одержуємо:

або

Якщо замінити, наприклад, друге рівняння нормуючою умовою, одержимо систему

розв’язуючи яку, знаходимо: ; .

Отже, за умови тривалого функціонування ринку цінних паперів граничні ймовірності падіння та росту цін дорівнюють відповідно 0,48 та 0,52. При цьому вони не залежать від початкового стану ринку.

Властивості поглинаючих ланцюгів Маркова. Такого типу ланцюги були визначені в п.4.2.3 як такі, що складаються лише з незворотних та поглинаючих станів. Система, що описується подібним ланцюгом Маркова, поступово переходить з незворотних станів у поглинаючі, знаходячись у незворотних станах деякий випадковий час. Очевидно, що коли такий ланцюг містить всього станів, з яких – поглинаючих, то при відповідній нумерації станів його матриця перехідних ймовірностей може бути зображена у вигляді

, (4.73)

де – одинична матриця з порядком ; - матриця з порядком , що складається з нулів; - матриця з порядком , яка задає ймовірності переходу з незворотних станів у поглинаючі; матриця з порядком , що складається з ймовірностей переходу між незворотними станами. Припустимо, що нас цікавлять характеристики:

• - середнє значення числа кроків , протягом яких система, яка вийшла з незворотного стану , перебуває в незворотному стані

• - середнє число кроків, протягом яких ланцюг Маркова перебуває в незворотних станах, якщо вихідним є незворотний стан

• - ймовірність того, що система, яка вийшла з незворотного стану попаде в поглинаючий стан .

Для поглинаючих ланцюгів Маркова, що задаються матрицями перехідних ймовірностей вигляду (4.73), справедливі наступні властивості:

1) значення визначаються як відповідні елементи матриці

, (4.74)

де - одинична матриця з порядком ; а - матриця ймовірностей переходу між незворотними станами з (4.73);

2) значення визначаються як відповідні компоненти вектора-стовпця

, (4.75)

де – вектор-стовпчик з порядком , компоненти якого дорівнюють одиниці, а - матриця, визначена співвідношенням (4.74):

Наслідок. Якщо початково ланцюг Маркова знаходиться в незворотному стані з ймовірністю , так що початковий розподіл ймовірностей незворотних станів ланцюга Маркова задається вектором , то середнє число кроків до поглинання визначається за формулою

; (4.76)

3) значення ймовірностей визначаються як відповідні елементи матриці

, (4.77)

де – матриця, визначена співвідношенням (4.74), а – матриця з (4.73), яка задає ймовірності переходу з незворотних станів у поглинаючі.

Властивості ланцюга Маркова, який містить множину незворотних станів J і замкнену (поглинаючу) множину зворотних станів . При аналізі такого типу ланцюгів нас можуть цікавити наступні питання:

• яка ймовірність того, що система, розпочинаючи блукання з незворотного стану, весь час буде знаходитися в множині незворотних станів ?

• як обчислити ймовірність того, що система, яка виходить з незворотного стану , коли-небудь досягне поглинаючу множину зворотних станів ?

Відповіді на ці питання містяться в наступних твердженнях:

Твердження 1. У скінченому ланцюгу Маркова ймовірність того, що система весь час буде знаходитися в множині незворотних станів дорівнює нулю.

Твердження 2. Ймовірність визначається як єдиний розв’язок системи лінійних рівнянь

. (4.78)

У цій системі сумування відбувається по всіх незворотних станах ланцюга, а – це ймовірність перейти з у будь-який зі станів множини за один крок.

Приклад 4.8а. Задача про розорення гравця: випадкове блукання з поглинанням. Граф переходів ланцюга Маркова має вигляд, зображений на рис. 4.6. Нагадаємо, що стани тут нумеруються, починаючи з нульового: . Очевидно, перед тим, як погоджуватися на той чи інший регламент гри, наш учасник (нехай це буде перший гравець) хотів би в першу чергу визначити ймовірність свого розорення (при грі до розорення).

Займемося розв’язанням цієї задачі. На мові ланцюга Маркова розорення нашого учасника означає його “поглинання” станом (він відповідає нульовому наявному капіталу гравця, тобто розоренню). Нескладний аналіз станів ланцюга показує, що він складається з незворотних станів (стани 1,2,…,N-1) і двох поглинаючих станів (стани 0 i ). Отже, розглядувана схема відноситься до категорії маpковських ланцюгів, які містять множину незворотних станів і замкнену (поглинаючу) множину зворотних станів . У нашому випадку ми маємо дві такі вироджені замкнені множини, кожна з яких складається з єдиного поглинаючого стану. Нас цікавитиме стан 0.

Розглянемо спочатку детальніше випадок п’яти станів . У цьому випадку матриця перехідних ймовірностей має вигляд

(4.79)

Для того, щоб записати матрицю у формі (4.73) перенумеруємо стани, залишивши нульовий стан нульовим, і зробивши четвертий стан першим, перший стан – другим і т.д. Тоді

(4.80)

Співставлення (4.80) з (4.73) показує, що

, .

Звідси одержуємо, що

і, як наслідок, матриця матиме вигляд

Пригадуючи інтерпретацію елементів матриці , бачимо, що середнє число кроків, на протязі яких ланцюг Маркова, відправляючись, наприклад, з третього стану, перебуває в четвертому стані, дорівнює .

Далі, на підставі формули (4.77) визначаємо матрицю :

.

Компоненти першого та другого векторів-стовпців матриці і будуть ймовірностями поглинання відповідно в нульовому та першому станах.

Дамо ігрову інтерпретацію отриманих результатів. Загальний капітал обох гравців дорівнює 4. Нехай кожний гравець на початку мав по 2 грошові одиниці. Це відповідає другому рядку матриці . Ймовірність розорення першого гравця – це перший елемент цього рядка, тобто вона дорівнює

Зауважимо тепер, що компоненти векторів ймовірностей поглинання можна визначити із системи рівнянь (4.78). Обчислимо на підставі цієї системи рівнянь ймовірності розорення першого гравця при різних значеннях його початкового капіталу. При цьому, виписуючи рівняння (4.78), будемо використовувати вихідні припущення щодо позначення станів розглядуваного ланцюга Маркова та зображення його матриці перехідних ймовірностей . У даному випадку маємо

Із врахуванням останніх співвідношень та (4.79) система (4.78) запишеться у вигляді

Розв’язуючи цю систему рівнянь відносно , знаходимо

Як бачимо отримані ймовірності збігаються з відповідними елементами першого стовпця матриці . Зрозуміло, що використовуючи систему рівнянь (4.78), можна обчислити ймовірності виграшу ( ) нашого учасника, які збігатимуться з відповідними елементами другого стовпця матриці .

Повертаємося до загального випадку нашої задачі. Для визначення ймовірності розорення першого гравця ( - початковий капітал цього гравця) складемо та розв’яжемо систему рівнянь (4.78). Очевидно, в даному випадку

так що система (4.78) має вигляд:

Розв’язуючи цю систему рівнянь відносно одержуємо:

Зауваження. У п.4.2. поза нашою увагою залишилися такі важливі розділи теорії марковських процесів як процеси з дискретними станами та неперервним часом і процеси з неперервними станами та неперервним часом. Такі процеси також знаходять широке застосування в економічній практиці. Зокрема, марковські процеси з дискретними станами та неперервним часом використовуються при моделюванні систем масового обслуговування. Далі, важливий клас марковських процесів з неперервними станами та неперервним часом становлять дифузійні процеси, які використовуються при побудові економіко-математичних моделей для задач, що зустрічаються у фінансовій та страховій математиці. Деякі з відзначених розділів читач може знайти в [4]. З іншими питаннями можна ознайомитися, зокрема, в такій літературі:

1. Феллер В. Введение в теорию вероятностей и ее приложения. Том 1, 2. – М.: Мир, 1984.

2. Леоненко М.М., Мішура Ю.С., Пархоменко В.M., Ядренко М.Я. Теоретико-ймовірнісні та статистичні методи в економетриці та фінансовій математиці. - К.: Інформтехніка, 1995. – 380 с.

3. Экономико-математическое моделирование: Учебник для студентов вузов / Под общ. ред. И.Н.Дрогобыцкого. – М.: Издательство “Экзамен”, 2004. – 800 с.

Рекомендована література: [4, c.183-201; 5, c.380-385].

Завдання для самоконтролю

Основні поняття, означення і відношення

Замість крапок запишіть таке продовження (доповнення) тексту, щоб отримати означення або твердження.

1. Випадковий процес з дискретними станами називається марковським, якщо … .

2. Випадкова послідовність називається ланцюгом Маркова, якщо для кожного кроку … .

3. Основними вихідними характеристиками ланцюгів Маркова є ймовірності … .

4. Початковим розподілом ймовірностей ланцюга Маркова називається розподіл ймовірностей … .

5. Ймовірністю переходу ланцюга Маркова називається … .

6. Якщо перехідні ймовірності ланцюга Маркова не залежать від номера кроку, то відповідний ланцюг Маркова називається … .

7. Якщо хоч би одна перехідна ймовірність ланцюга Маркова змінюється зі зміною кроку, то ланцюг Маркова називається … .

8. Елементи кожного рядка матриці переходу ланцюга Маркова невід’ємні та задовольняють умову … .

9. Квадратна матриця називається стохастичною, якщо її елементи задовольняють умови … .

10. Якщо для однорідного ланцюга Маркова задана матриця перехідних ймовірностей , то матриця , яка складається з ймовірностей переходу за кроків, виражається через матрицю рівністю … .

11. Якщо для однорідного ланцюга Маркова задані матриця перехідних ймовірностей та початковий розподіл ймовірностей, то абсолютні ймовірності станів на –му кроці визначаються за допомогою рекурентної формули … .

12. Ймовірність першого досягнення стану ланцюга Маркова при його виході зі стану можуть бути обчислені через ймовірності переходу внаслідок рекуррентного застосування формул … .

13. Ймовірність того, що, починаючи зі стану , ланцюг Маркова коли-небудь досягне стану визначається за формулою … .

14. Середнє число кроків до першого досягнення ланцюгом Маркова стану при виході зі стану виражається формулою … .

15. Кажуть, що стан ланцюга Маркова досягається зі стану , якщо … .

16. Деяка підмножина станів ланцюга Маркова називається замкненою (або поглинаючою), якщо … .

17. Деякий стан ланцюга Маркова називається зворотним, якщо ймовірність повернення для нього дорівнює … , і незворотним, якщо ця ймовірність … .

18. Стан ланцюга Маркова називається періодичним з періодом , якщо … .

19. Деякий стан ланцюга Маркова називається ергодичним, якщо … .

20. Ланцюг Маркова називається незвідним, якщо … .

21. Ланцюг Маркова називається ергодичним, якщо … .

22. Ланцюг Маркова називається поглинаючим, якщо … .

23. Якщо скінченний однорідний ланцюг Маркова ергодичний, то існують … ймовірності.

24. Якщо граничні ймовірності ланцюга Маркова існують, то вони визначаються з наступної системи рівнянь … .

25. Ймовірності того, що ланцюг Маркова, який виходить з незворотного стану, коли-небудь досягне поглинаючу множину зворотних станів визначається як єдиний розв’язок системи лінійних рівнянь … .

Тести

Запишіть на бланку відповідей номер завдання і коди (порядкові номери або літери), що відповідають тим варіантам відповідей, які вважаєте правильними.

1. Розмічений граф станів системи , в якій відбувається марковський процес з дискретними станами та дискретним часом, зображено на рисунку 4.9.

Записати матрицю перехідних ймовірностей для розглядуваного ланцюга Маркова.

Варіанти відповідей: 1. . 2. . 3.

2. Для якого значення наведена нижче матриця є стохастичною?

Варіанти відповідей: 1. 0,1; 2. 0,2; 3. -0,2.

3. Припустимо, що в умовах тесту 1, початковий розподіл ймовірностей має вигляд:

.

Обчислити абсолютну ймовірність стану ланцюга Маркова після 1-го кроку.

Варіанти відповідей: 1. 0,5; 2. 0,65; 3. 0,35.

4. Розглянемо матрицю перехідних ймовірностей ланцюга Маркова

Чи існує для ланцюга Маркова стаціонарний розподіл.

Варіанти відповідей: 1. так. 2. ні.

5. Розглянемо ланцюг Маркова з трьома станами та матрицю перехідних ймовірностей

.

Чи є всі три стани даного ланцюга Маркова періодичними ? Якщо так, то яким є період цих станів ?

Варіанти відповідей: 1. ні. 2. так і 3. так і