Методичні вказівки до рішення завдання № 4.1

Результати розрахунків задачі треба подати у формі табл. 4.5. У даній таблиці наведено приклад, коли число n=10, число експертів m=3, систему оцінки в балах у прикладі взято рівною п’яти.

Таблиця 4.5

Результати розрахунків

№ рядка	Експерт	Номери об’єктів
		1	2	3	4	5	6	7	8	9	10
1	Експерт 1	3	5	4	5	4	5	2	2	5	1
2	Експерт 2	3	2	3	3	4	4	1	2	2	2
3	Експерт 3	2	4	5	5	5	4	2	1	4	2
4	Експерт 1	7	1-4	5-6	1-4	5-6	1-4	8-9	8-9	1-4	10
5	Експерт 2	3-5	6-9	3-5	3-5	1-2	1-2	10	6-9	6-9	6-9
6	Експерт 3	7-9	4-6	1-3	1-3	1-3	4-6	7-9	10	4-6	7-9
7	Експерт 1	7	2,5	5,5	2,5	5,5	2,5	8,5	8,5	2,5	10
8	Експерт 2	4	7,5	4	4	1,5	1,5	10	7,5	7,5	7,5
9	Експерт 3	8	5	2	2	2	5	8	10	5	8
10		19	15	11,5	8,5	9	9	26,5	26	15	25,5
11		2,5	-1,5	-5	-8	-7,5	-7,5	10	9,5	-1,5	9
12		6,25	2,25	25	64	56,25	56,25	100	90,25	2,25	81

У табл. 4.5 в перших трьох рядках подано оцінки об’єктів у балах (в п’ятибальній системі), виставлені експертами.

Так, наприклад, перший експерт виставив п’ять балів об’єктам 2, 4, 6, 9, чотири бали – об’єктам 3 та 5 і т. д.

Рядки 4...6 табл. 4.5 містять інформацію про місце кожного об’єкта в ряді інших.

Так, в рядку 4 об’єкти – 2, 4, 6, 9 – розділили місця з першого по четверте, об’єкти 3 та 5 – місця п’яте та шосте, об’єкт 1 зайняв сьоме місце, об’єкти 7 та 8 – розділили восьме та дев’яте місця і, нарешті, об’єкт 10 зайняв десяте місце. Теж саме зроблено у рядках 5 та 6.

Очевидно, що кількість місць об’єктів дорівнює числу n (в даному разі – 10).

У наступних рядках 7...9 містяться стандартизовані ранги . Стандартизовані ранги з’являються у тому разі, коли декілька об’єктів мають однакові оцінки в балах. Так, в четвертому рядку вони мають з’явитися у об’єктів 2, 4, 6, 9, потім у об’єктів 3 та 5, далі у об’єктів 7 та 8. Об’єкти 1 та 10 не мають стандартизованих рангів, їхній ранг співпадає із займаним місцем.

розраховується як середнє значення місця, займаного об’єктами з однаковими оцінками, отримане як сума місць, займаних об’єктами, поділена на кількість об’єктів з однаковими оцінками. Так, у сьомому рядку для об’єктів 2, 4, 6 та 9, що займають місця 1...4:

Для об’єктів 3 та 5, що займають місця 5 та 6:

Для об’єктів 7 та 8, що займають місця 8 та 9:

Аналогічно виконуються розрахунки для другого та третього експертів (рядки 8 та 9 табл. 4.5).

Сума рангів кожного -го експерта, отримана усіма n об’єктами, дорівнює сумі чисел натурального ряду від 1 до n:

.

Тут – ранг і-го об’єкта, отриманий j-м експертом.

Рядок 10 містить суми рангів , виставлених усіма m експертами по кожному і-му об’єкту:

.

У прикладі m = 3.

Далі розраховується квадрат відхилення суми рангів від середнього значення сум по кожному об’єкту:

(4.1)

Тут

.

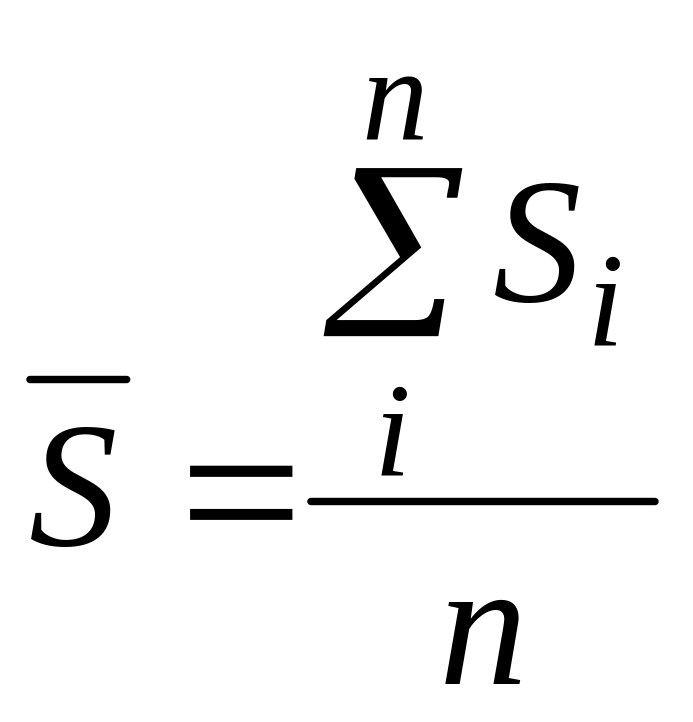В рядку 11 подано значення , а в рядку 12 – значення .

У прикладі .

Значення можна розрахувати за формулою (4.2):

(4.2)

.

Рядок 12 містить значення , отримані за виразом (4.1).

Після отримання табл. 4.5 розраховується коефіцієнт конкордації за формулою (4.3):

(4.3)

де .

У нашому прикладі .

Формулою (4.3) можна користуватися лише в разі, якщо немає стандартизованих рангів . За їх наявності належить використовувати формулу (4.4):

(4.4)

де

, (4.5)

– число повторень однакових рангів у j-го експерта,

– номер (індекс) рангів, що повторюються.

Для розглядуваного в табл. 4.5 прикладу стандартизовані ранги існують, отже, скористуємося формулою (4.4).

Обчислимо , , .

Для першого експерта розглядаємо рядок 7. Маємо чотири повторення рангу , два повторення рангу , два повторення рангу . Отже, в сумі буде три доданки (маємо три групи рангів, що повторюються):

.

Для другого експерта (рядок 8) маємо два повторення рангу , три повторення рангу , чотири повторення рангу . Отже,

.

Аналогічно для третього експерта:

.

.

Критерій визначимо за формулою (4.6):

, (4.6)

.

Звертаючись до табл. 4.4, знайдемо при n = 10 в рядку n–1 = 9 значення ймовірності того, що думки експертів погоджені. Ця ймовірність складає понад 95 %.