Завдання № 3

Завдання розраховано на виконання протягом одного практичного заняття – 2 години.

Мета роботи: визначення показників роботи системи обслуговування (відновлення роботи обладнання, яке потребує ремонту) як системи масового обслуговування, визначення параметрів системи аварійного відновлення.

Таблиця 3.1

Вихідні дані

Остання цифра № студентського квитка	0	1	2	3	4	5	6	7	8	9
Число одиниць устаткування,	6	5	5	6	7	6	5	6	7	5
Число каналів обслуговування,	3	4	3	4	5	3	2	3	4	3
Передостання цифра № студентського квитка	0	1	2	3	4	5	6	7	8	9
Інтенсивність відмов, , 1/год	0,03	0,04	0,07	0,02	0,06	0,04	0,05	0,03	0,04	0,05
Інтенсивність відновлення, , 1/год	0,06	0,09	0,18	0,05	0,15	0,1	0,13	0,07	0,12	0,2

Методичні вказівки до рішення завдання №3

Під аварійним відновленням будемо розуміти ремонт (відновлення) устаткування після виникнення відмови.

Розглянемо наступну модель аварійного відновлення.

Об'єкт має m одиниць однотипного устаткування. У процесі експлуатації кожна з них утворить потік вимог на відновлення з інтенсивністю відмов . Т – середній час наробітку на відмову.

Є n ремонтних бригад. При виході з ладу будь-якої одиниці устаткування вона приймається на обслуговування кожною з вільних ремонтних бригад і повністю відновлюється після кожного ремонту.

Час відновлення:

, (3.1)

де – інтенсивність відновлення .

Після ремонту устаткування повертається в лад і знову стає джерелом відмов.

Кожна бригада ремонтує тільки одну одиницю устаткування. Будемо вважати, що кожна бригада є каналом обслуговування. Вся система має n каналів обслуговування. При зайнятості всіх каналів обслуговування надходжувані заявки на ремонт утворять чергу. Перша бригада, що звільнилася, приймає на відновлення перше устаткування, що прийшло у чергу.

Для розрахунку показників системи масового обслуговування необхідно визначити всі можливі стани системи й імовірності перебування системи в цих станах.

Можливі стани системи представлені в табл. 3.2.

Таблиця 3.2

Можливі стани системи і їхні характеристики

Стан	Характеристика станів	Імовірність стану	Кількість
			Устаткування			Рем. бригади
			що працює	що простоює		що працюють	що простоюють
				в ремонті	в черзі
	Все устаткування справне			0	0	0
	1 од. устаткування відмовила, черги немає			1	0	1
	2 од. устаткування відмовили, черги немає			2	0	2
-	---	---	---	---	---	---	---
	од. устаткування відмовили, черги немає				0		0
	од. устаткування відмовили, 1 од. в черзі				1		0
-	---	---	---	---	---	---	---
	од. устаткування відмовили, од. в черзі		0				0

Тут використані позначення:

– k-ий можливий стан системи;

– імовірність перебування системи в k-му стані.

Імовірність деякого k-го стану може бути знайдена по рекурентній формулі:

(3.2)

Формула (3.2) показує, що ймовірність переходу системи зі стану k-1 у наступний k-ий дорівнює ймовірності попереднього (k-1)-го стану , помноженої на інтенсивність переходу з попереднього стану в наступний і діленої на інтенсивність повернення з наступного стану в попередній.

Всі ймовірності , що цікавлять, виражають через з використанням співвідношень (3.3) і (3.4).

У вираженні (3.3) обчислюється ймовірність знаходження системи в стані , коли поступило k заявок на обслуговування (k одиниць устаткування відмовило), причому , тобто немає черги.

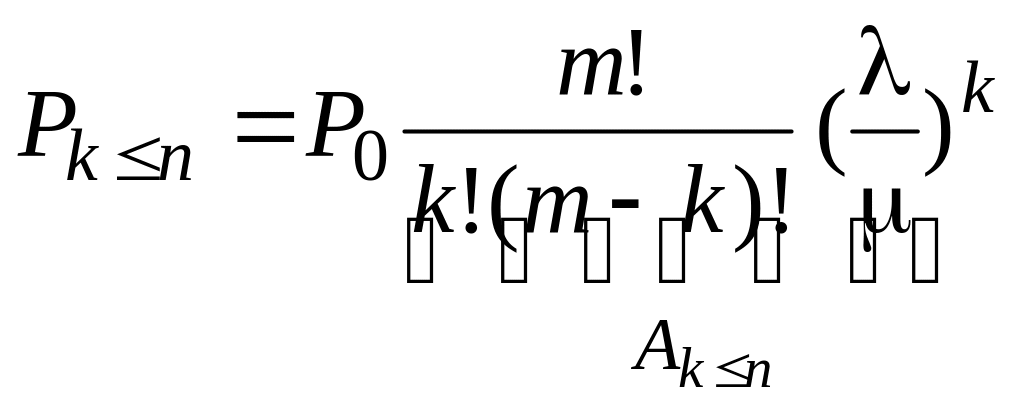(3.3)

У випадку, коли в системі організується черга з l одиниць, , тобто коли , використовується вираз 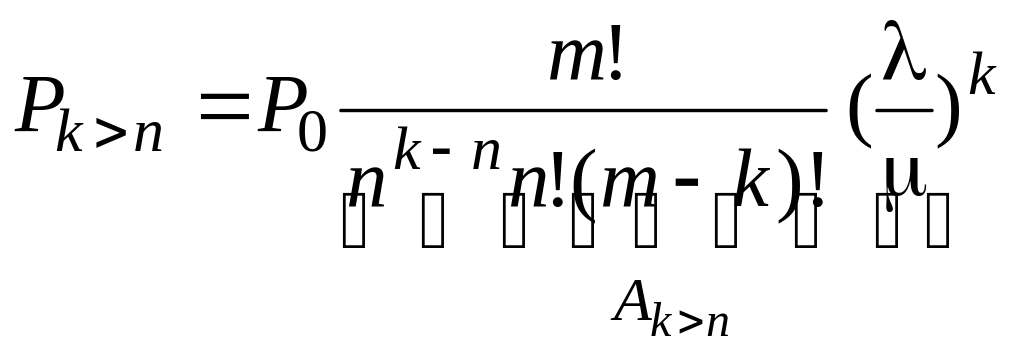(3.4):

(3.4)

Для визначення значення користуються нормувальною умовою (3.5):

(3.5)

Позначивши у формулі (3.3) через другий співмножник у правій частині, а у формулі (3.4) другий співмножник позначивши через , отримаємо вираз (3.6) для розрахунку ймовірності :

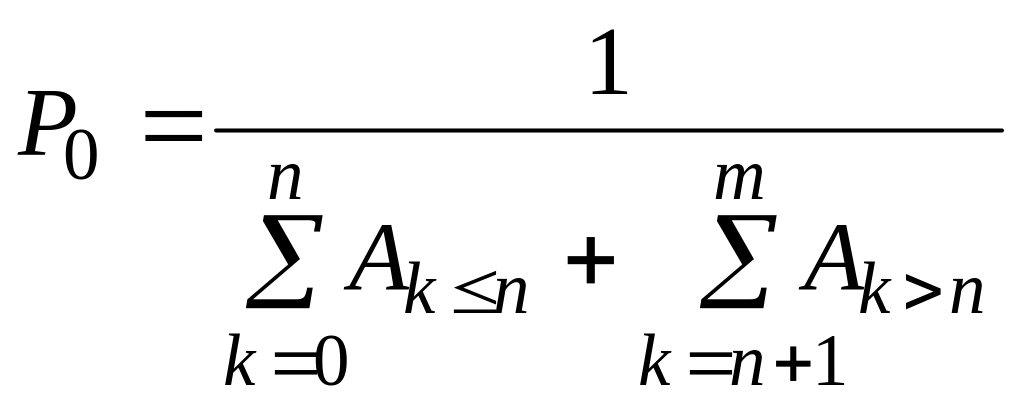(3.6)

Вираз (3.6) можна представити у вигляді:

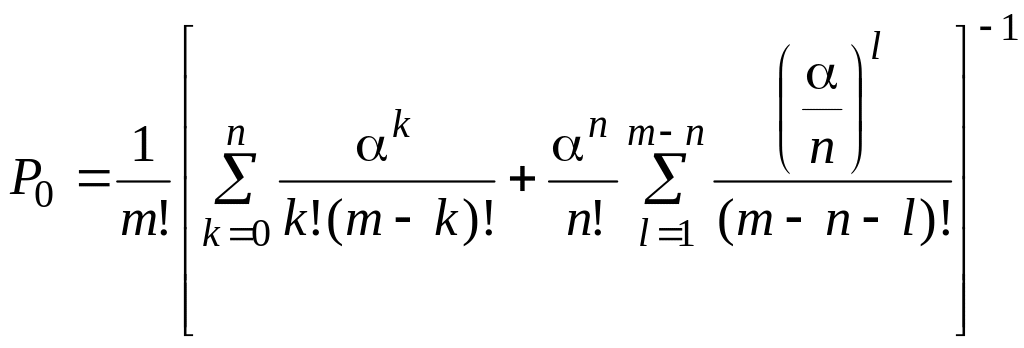, (3.7)

Крім розрахунку ймовірностей стану системи обслуговування, інтерес представляють також наступні показники:

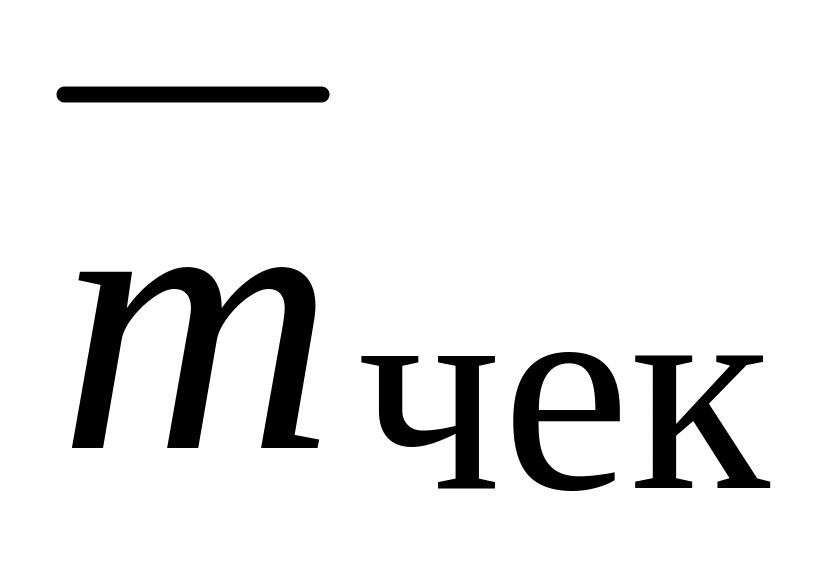• – середнє число вимог (одиниць устаткування), що очікують ремонту (відновлення):

(3.8)

• – середнє число вимог, що перебувають на обслуговуванні, або кількість працюючих ремонтних бригад (засобів) :

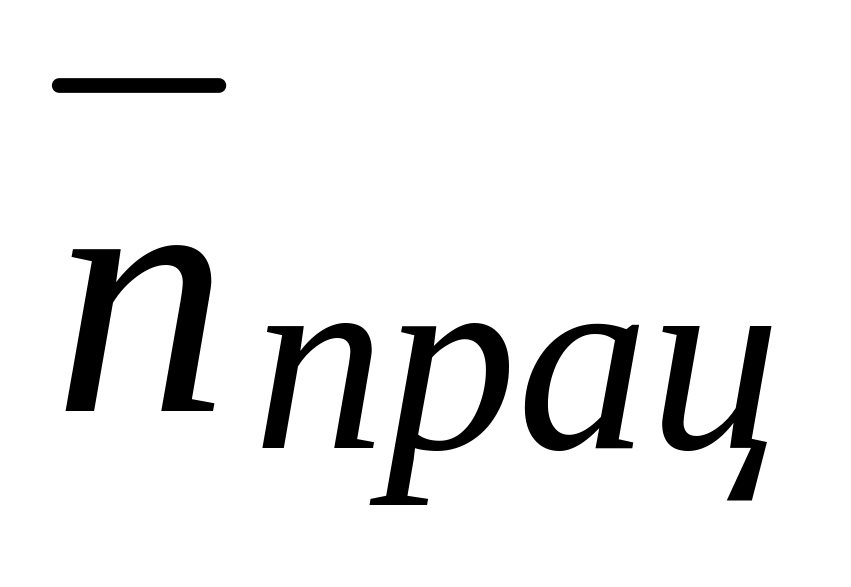(3.9)

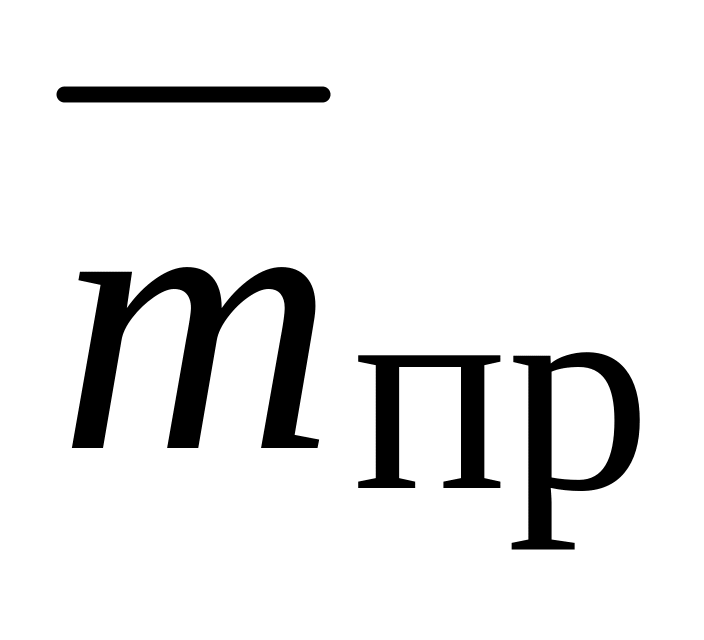• – середнє число устаткування, що простоює:

(3.10)

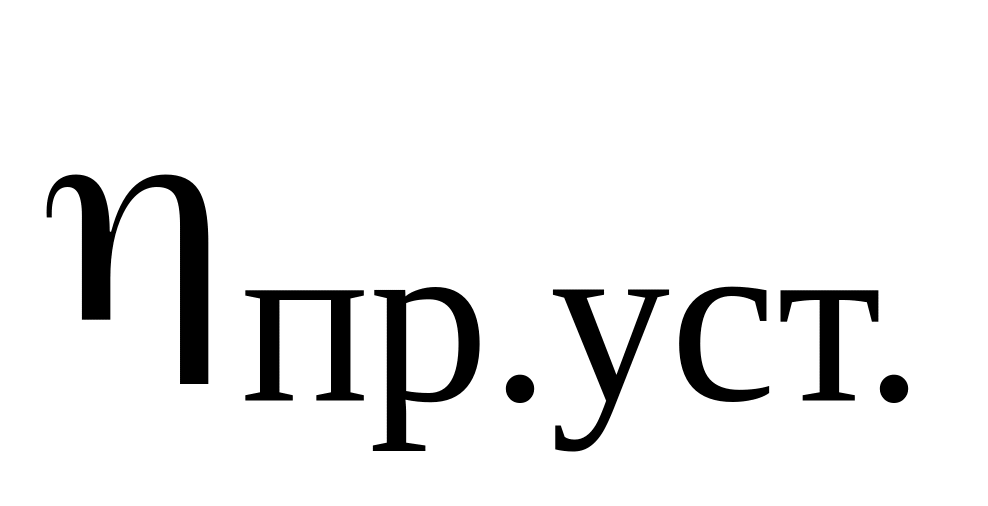• – коефіцієнт простою устаткування:

(3.11)

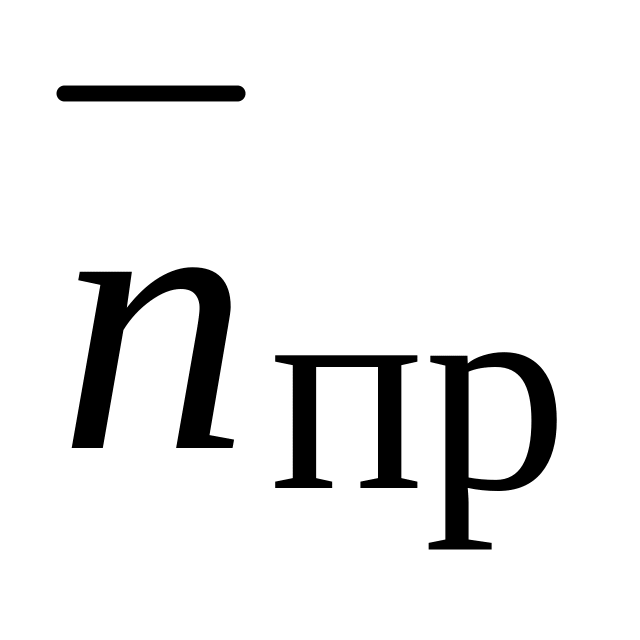• – середнє число бригад, що простоюють:

(3.12)

• – коефіцієнт простою ремонтних засобів:

(3.13)

Таким чином, розрахунки по формулах (3.3) ... (3.13) надають можливість повністю оцінити ситуацію, що характеризує працездатність системи й прийняти необхідні управлінські рішення, пов'язані з поліпшенням показників ефективності функціонування розглянутої системи масового обслуговування й показників якості обслуговування споживачів.

Приклад розрахунку

Задано =5; =3; =0,04 ; =0,08 .

Визначити значення всіх , k = 0-5, а також , , , , ,

Для розрахунку , , користуємося формулою (3.3), а для розрахунку , - формулою (3.4).

Розрахуємо

Запишемо вираз для всіх , k = 1-5:

k = 1;

k = 2;

k = 3;

k = 4;

k = 5;

Значення розраховуємо по формулі (3.3): k = 0;

Розрахунок значення виконаємо за формулою (3.6):

Тепер можна отримати значення :

.

Для перевірки правильності отриманого рішення скористаємося умовою (3.5):

.

Розрахуємо інші характеристики системи.

Тут k = 4,5.

.

Таким чином, отримані результати є основою для визначення рівня якості надаваних послуг й обслуговування.

Як бачимо, маємо ненадійне устаткування ( ). Крім того, за отриманим значенням , , , , можна зробити висновок про досить неефективне використання як устаткування, так й обслуговуючих бригад.