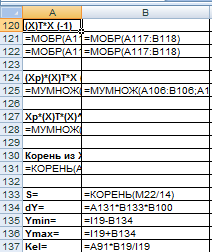
- •Ход работы:
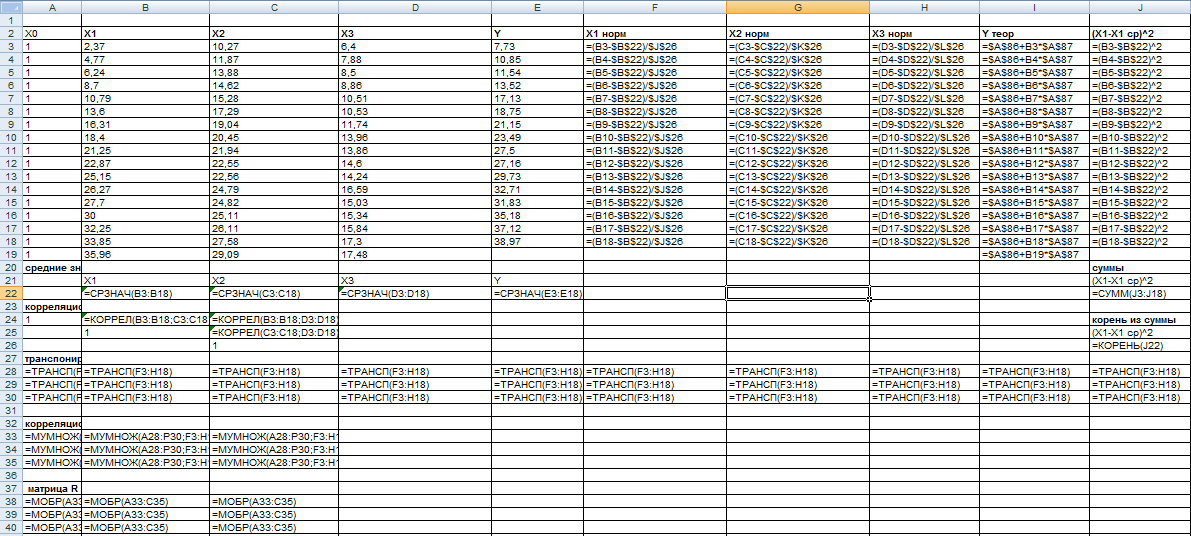
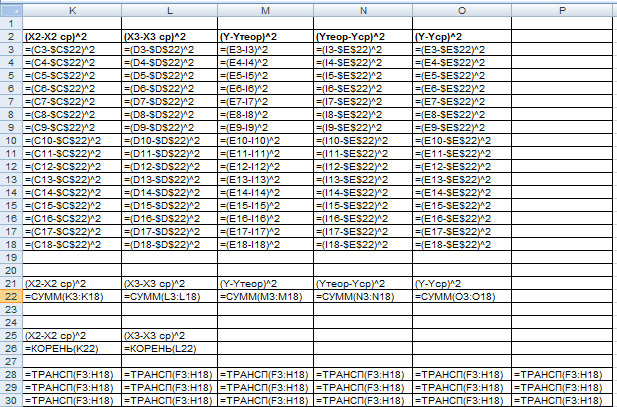
- •Исходные данные
- •Построение корреляционной матрицы
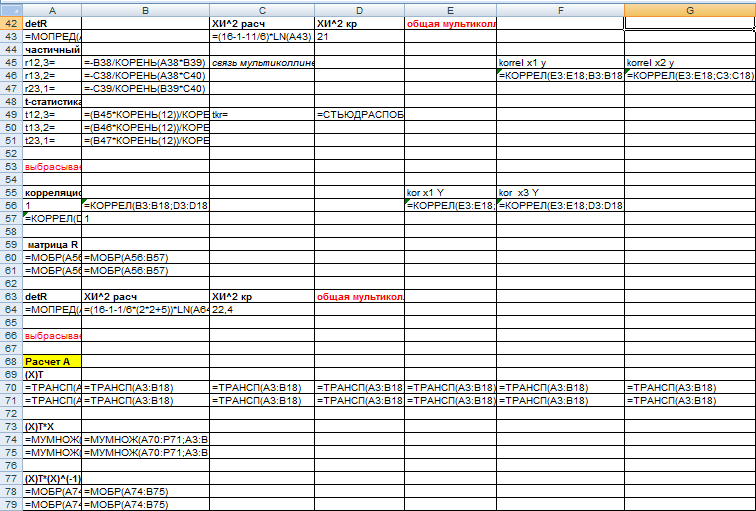
- •Тест на наличие мультиколлинеарности
- •Проверяется наличие или отсутствие общей мультиколлинеарности в модели при помощи χ2-критерия Пирсона.
- •Так как в модели имеет место мультиколлинеарность, необходимо выяснить между какими факторами она присутствует
- •Второй этап теста на мультиколлинеарность
- •Оценок параметров модели
Оценок параметров модели
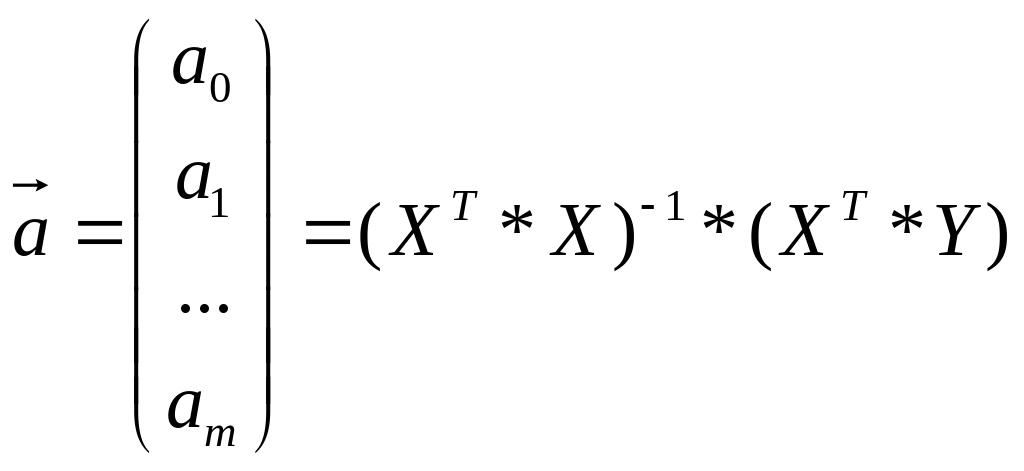
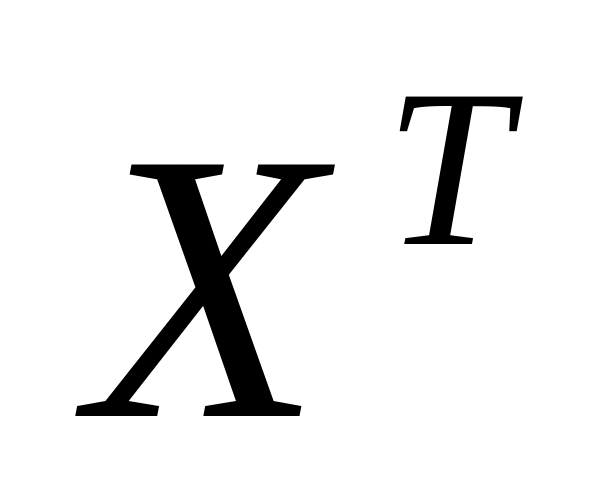 - транспонирование матрицы
Х;
- транспонирование матрицы
Х;
Матрицу рассчитываем в блоке А70:Р71. =ТРАНСП(A3:B18)
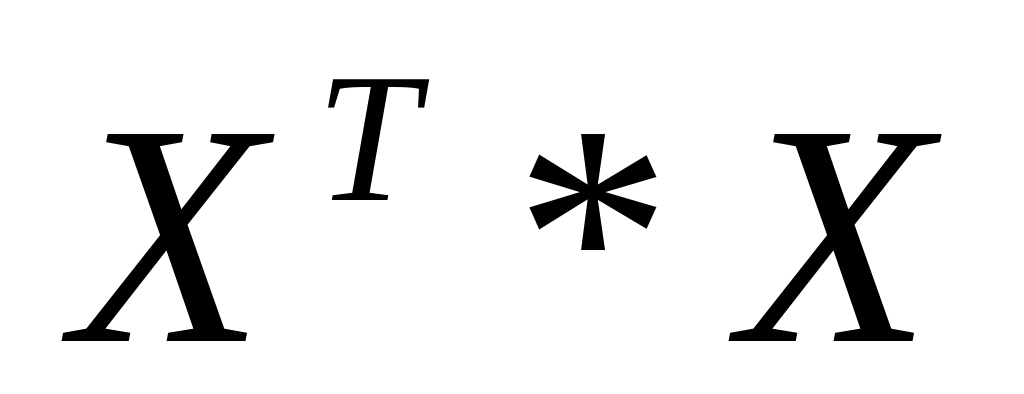 -
результат (1) умножить на матрицу Х;
-
результат (1) умножить на матрицу Х;
Матрицу рассчитываем в блоке А74:В75.
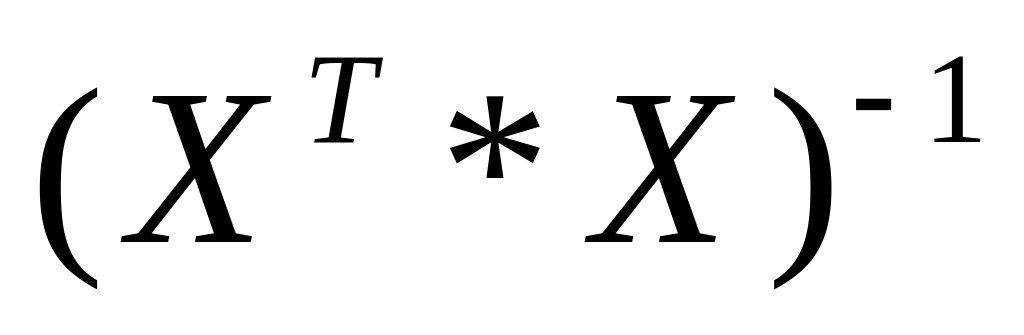 -
найти обратную матрицу к результату
(2);
-
найти обратную матрицу к результату
(2);
Матрицу рассчитываем в блоке А78:В79.
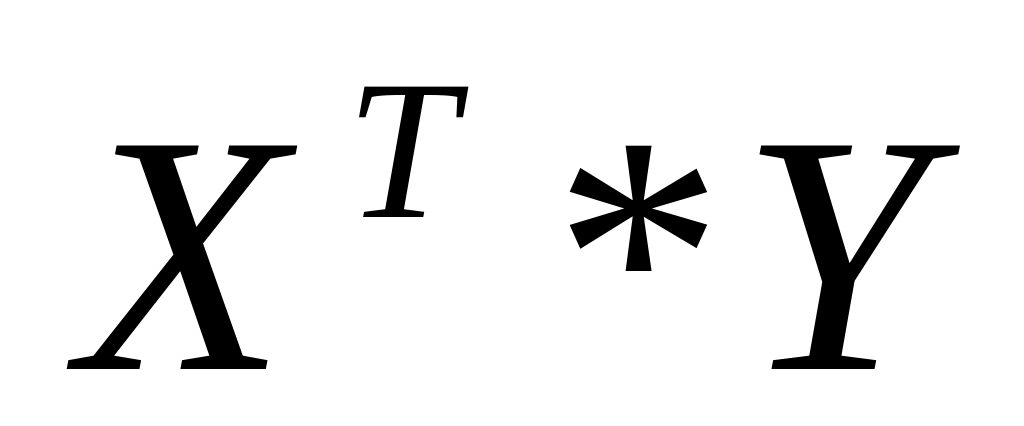 -
результат (1) умножить на матрицу У;
-
результат (1) умножить на матрицу У;
Матрицу рассчитываем в блоке А82:А83.
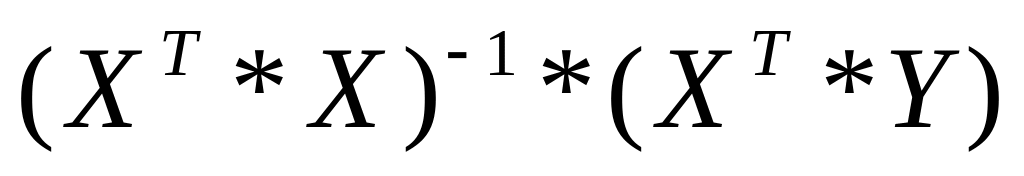 - перемножить результаты (3) и (4);
- перемножить результаты (3) и (4);
Матрицу рассчитываем в блоке А86:А87.
А |
|
5,620613526 |
a0 |
0,979735737 |
a1 |
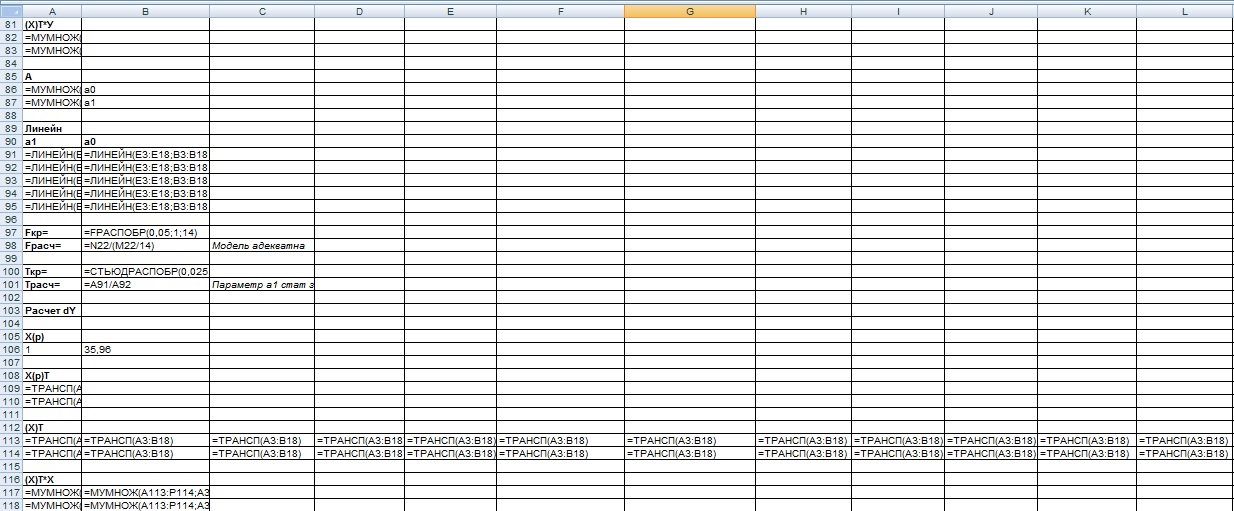
Запустим функцию ЛИНЕЙН
Таблица 6
Результат работы функции ЛИНЕЙН
0,986214348 |
5,563223849 |
0,017806658 |
0,373705586 |
0,995456687 |
0,699129177 |
3067,452088 |
14 |
1499,314158 |
6,842942483 |
Проверка параметра на значимость
Проверяется только коэффициенты при Х.
Если
![]() ,
параметр ai
статистически значимый
,
параметр ai
статистически значимый
tкр находят при помощи функции СТЬДРАСПРОБР:
- уровень значимости – 0,05/2;
- степени свободы – n-m-1=16-1-1=14
tкр= 2,509569405.
![]() ,
,
где Sa-стандартная ошибка по модулю
![]() =
55,24043794
=
55,24043794
Так как , параметр a1 статистически значимый.
теоретические значения показателя
В ячейку I3 вводим формулу =$A$86+B3*$A$87 и копируем ее.
F-статистика Фишера проверки модели на адекватность
Если Fрасч>Fкр, то модель адекватна статистическим данным (хотя бы один из параметров при Х не равен нулю).
- F-расчетное:
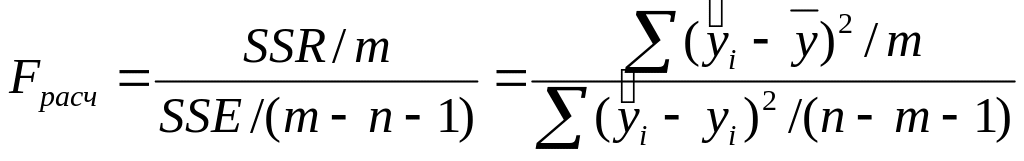
![]() находим в ячейке B98 по
формуле =N22/(M22/14)
находим в ячейке B98 по
формуле =N22/(M22/14)
= 3051,505984
- F-критическое
Fкр находится с помощью функции FРАСПОБР
уровень значимости – 0,05;
степень свободы 1 – m=1;
степень свободы 2 – n-m-1=16-1-1=14
Fкр находим в ячейке В97.
Fкр= 4,600109908
Так как Fрасч>Fкр, то модель адекватна статистическим данным.
Точечный прогноз:
![]() .
.
В ячейку І19 вводим формулу =$A$86+B19*$A$87
Расчет доверительного интервала
![]() ,
где
,
где
![]()
Найдем![]()
1. - транспонирование матрицы Х;
2. - результат (1) умножить на матрицу Х;
3. - найти обратную матрицу к результату (2);
4.
![]() -
-
![]() умножить на результат (3)
умножить на результат (3)
![]()
5. Расчитываем
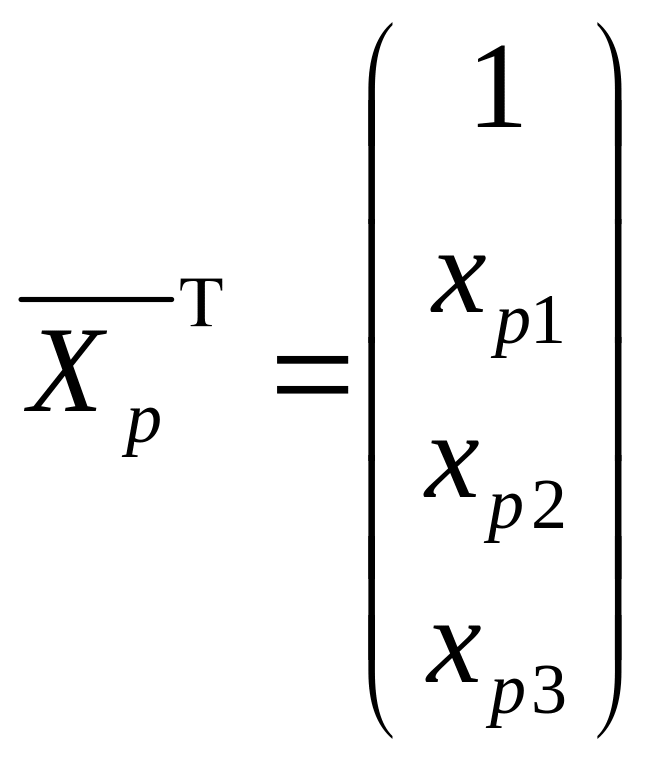 .
.
6.
![]() -
результат (4) умножить на
-
результат (4) умножить на
![]()
7.
![]() .
.
8. Рассчитываем
![]() .
В ячейку В133 вводим формулу =КОРЕНЬ(M22/14)
.
В ячейку В133 вводим формулу =КОРЕНЬ(M22/14)
9.
![]() .
В ячейку В134 вводим формулу =A131*B133*B100
.
В ячейку В134 вводим формулу =A131*B133*B100
Доверительный интервал:
Ymin= 39,9703959
Ymax = 41,73342534
Частичный коэффициент эластичности рассчитываем по формуле:
![]()
Частичный коэффициент эластичности показывает на сколько процентов изменится показатель Y при неизмененных значениях других факторов, если X1 изменится на 1%.
![]()
Выводы:
Между факторами Х1, Х2 и Х3 существует мультиколлинеарность. Выбросим факторы Х2, Х3, так как они менее всего влияют на показательУ.
Так как Fрасч>Fкр, то с надежностью 0,95 можна считать модель
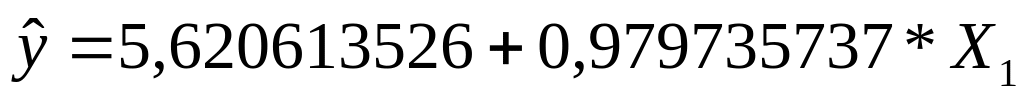 адекватной статистическим данным. На
основании этой модели можно делать
экономические выводы.
адекватной статистическим данным. На
основании этой модели можно делать
экономические выводы.С надежностью 0,95 можно считать, что влияние фактора Х1 на показатель У значительное.
4. Прогнозное значение показателя с надежностью 0,95 будет находится в промежутке [39,9703959; 41,73342534]
5. При изменении факторов в точке пргноза Х1р на 1 % показатель У изменится на 0,862414917 %.
Приложение
Таблица 1
Множественная линейная регрессия
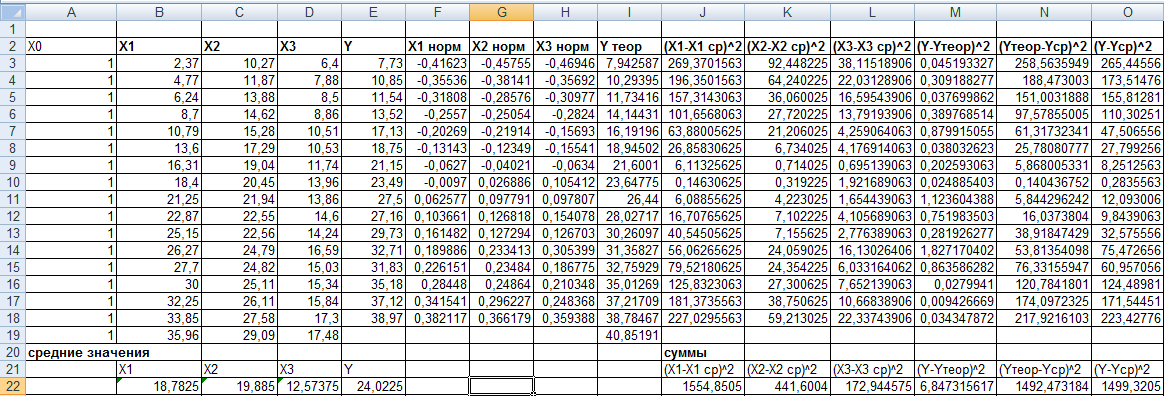
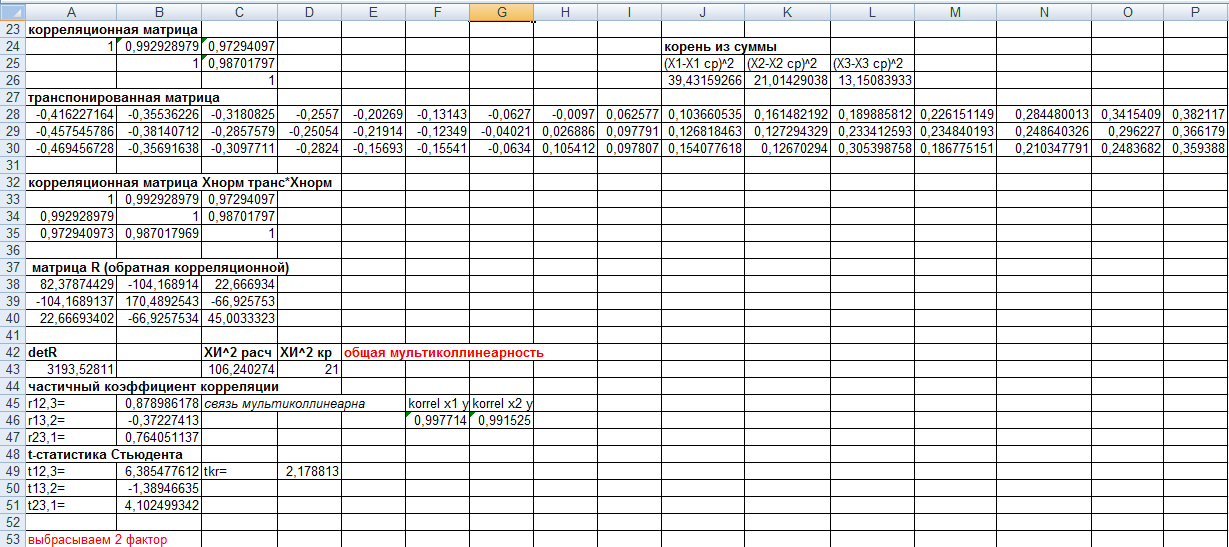
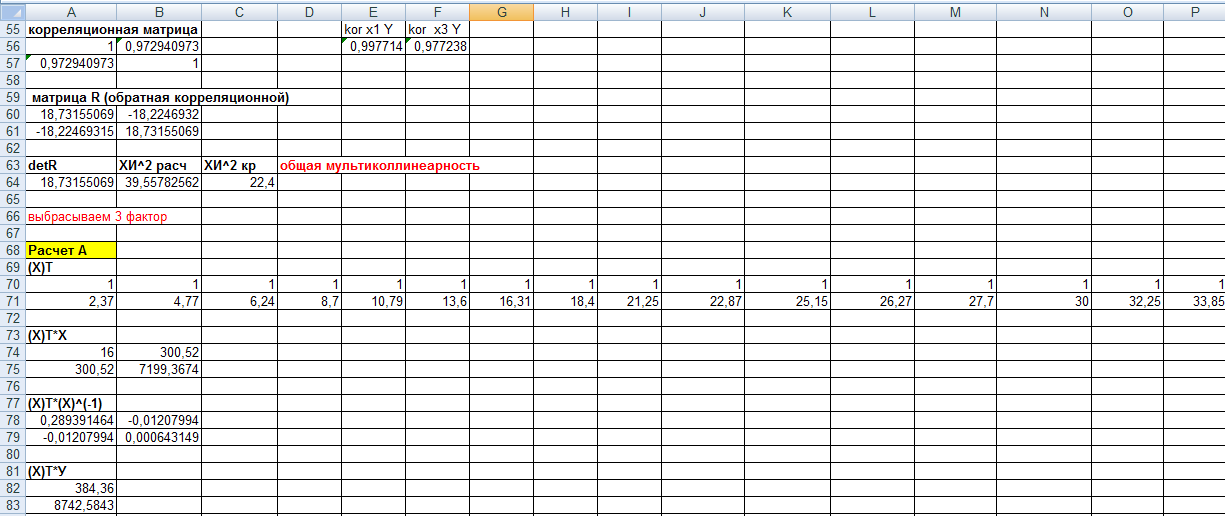
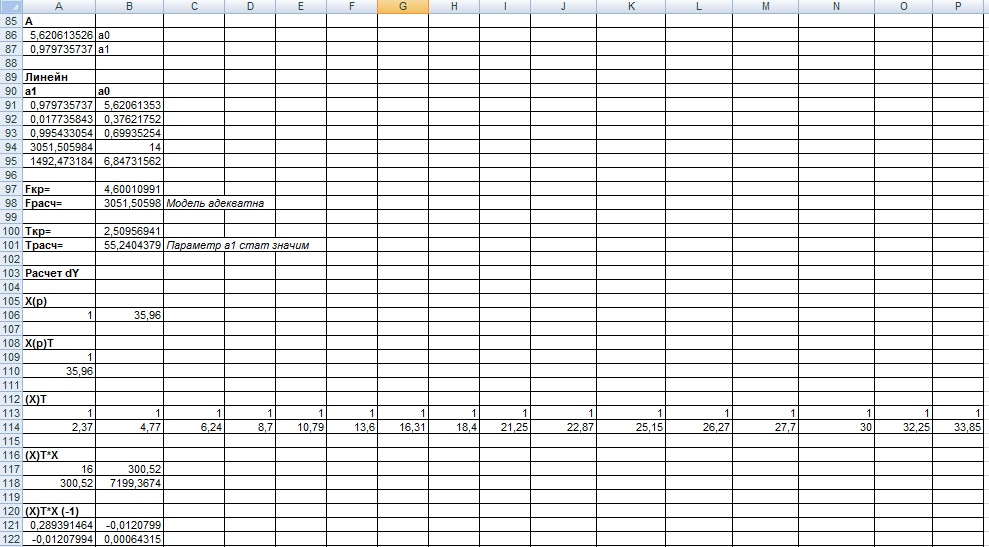

Таблица 2
Режим формул