2. Геометрическое распределение.

Случайная величина Х имеет геометрическое распределение, если

, k=0,1,2,…, 0<p<1, q=1-p (4.26)

Геометрическое распределение имеет случайная величина Х, равная числу испытаний до первого успеха с вероятностью успеха в единичном испытании р.

Математическое ожидание геометрического распределения .

Дисперсия дискретной случайной величины, распределенной по геометрическому закону равна .

Стандартное отклонение .

4. Биномиальное распределение.

Целочисленная случайная величина Х, принимающая значения от 0 до n, имеет биномиальное распределение, если задаются формулой Бернулли.

Х	0		k		n
Р					

.

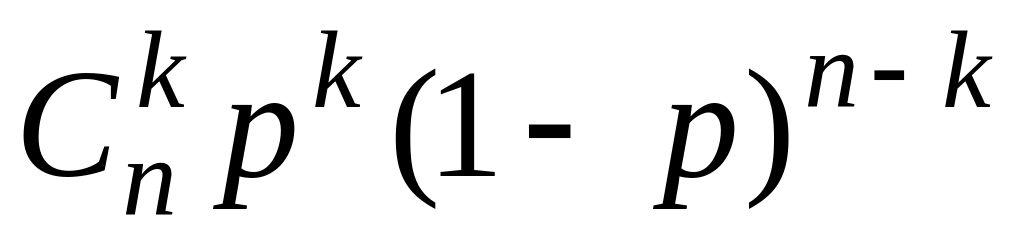
Математическое ожидание биномиального распределения .

Дисперсия дискретной случайной величины, распределенной по биномиальному закону равна .

Стандартное отклонение .

5. Распределение Пуассона.

При больших значениях n вычисление вероятностей по формуле Бернулли становится затруднительным. Если формулу Бернулли заменяют приближенной асимптотической формулой Пуассона.

(4.27)

Математическое ожидание распределения Пуассона: .

Дисперсия дискретной случайной величины, распределенной по закону Пуассона равна .

Стандартное отклонение .

Примеры решения задач

4.1. Найти математическое ожидание дискретной слу­чайной величины X, заданной законом распределения:

а) Х –4 6 10 . б) X 0,21 0,54 0,61

р 0,2 0,3 0,5 р 0,1 0,5 0,4.

Решение: а) Математическое ожидание равно сумме произ­ведений всех возможных значений Х на их вероятности:

М(Х)=-4 ^. 0,2 +6 ^. 0,3+10 ^. 0,5=6.

4.2. Найти математическое ожидание и дисперсию случайной вели­чины Z, если известны математические ожидания и дисперсии Х и Y: Z=X-2Y, M(X)=5, M(Y)=3, D(X)=2, D(Y)=4.

Решение: Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожи­даний слагаемых, постоянный множитель можно вынести за знак математического ожидания), получим

М (Z)= М (X -2Y) = М (X) - М (2Y) = М (X) - 2M(Y) = =5-2^.3=-1.

Используя свойства дисперсии (дисперсия разности независимых случайных величин равна сумме дисперсий слагаемых, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат), получим

D(Z)=D(X-2Y)=D(X)+4D(Y)=2+4^.4=18.

4.3. Охранное устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

Решение: Возможные значения случайной величины Х={0,1,2,3}. Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, p=0,1, следовательно q=1-p=0,9, получим:

Контроль: 0,729+0,243+0,027+0,001=1.

Напишем биномиальный закон распределения:

Х	0	1	2	3
р	0,729	0,243	0,027	0,001

4.4. Учебник по теории вероятностей издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Составить первые 3 члена закона распределения дискретной случайной величины Х – числа бракованных книг в тираже.

Решение: Возможные значения Х равны {0, 1, 2, 3, …, k}. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность р мала, поэтому воспользуемся распределением Пуассона (4.32):

По условию, n=100000, p=0,0001, следовательно, q=0,9999 (npq=9,999). Найдем . Вероятности возможных значений будут равны:

Закон распределения запишется в следующем виде:

Х	0	1	2	…
р	0,000045	0,00045	0,00225	…

4.5. Производится 3 выстрела с вероятностями попадания в цель, равными р₁=0,4; р₂=0,3 и р₃=0,6. Найти математическое ожидание общего числа попаданий.

Решение: Число попаданий при одном выстреле есть случайная величина Х₁, возможные значения которой 1 (попадание) с вероятностью р₁=0,4 и 0 (промах) с вероятностью q₁=1-0,4=0,6. Математическое ожидание М(Х₁)=0,4. Аналогично найдем математические ожидания М(Х₂)=0,3 и М(Х₃)=0,6.

Общее число попаданий есть также случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов: Х=Х₁+Х₂+Х₃. Тогда математическое ожидание общего числа попаданий равно

М(Х)=М(Х₁+Х₂+Х₃ )=М(Х₁)+М(Х₂)+М(Х₃)=0,4+0,3+0,6=1,3 (попаданий).

4.6. Дискретная случайная величина Х задана зако­ном распределения:

Х 1 2 4

р 0,1 0,3 0,6

Найти центральные моменты первого, второго, третьего и четвертого порядков.

Решение: Центральный момент первого порядка равен нулю =0.

Для вычисления центральных моментов удобно воспользоваться формулами, выражающими центральные моменты через начальные, поэтому предварительно найдем начальные моменты

₁=М(Х) =1 ^. 0,1+ 2 ^. 0,3- 4 ^. 0,6=3,1.

₂=M(X²)=1 ^. 0,1+ 4 ^. 0.3+ 16 ^. 0,6=10,9;

₃=М(X^З)=l ^. 0,1+ 8 ^. 0,3+64 ^. 0,6=40,9;

₄=M(X⁴)=1 ^. 0,1 +16 ^. 0,3+256 ^. 0,6=158,5.

Найдем центральные моменты.

=10,9 - 3,1²= 1,29;

= 40,9 – 3 ^. 3,1 ^. 10,9 +2 ^. 3,1³= -0,888;

=

=158,5 – 4 ^. 40,9 ^. 3,1+6 ^. 10,9 ^. 3,1² – 3 ^. 3,1⁴=2,7777.