
- •Глава 1. Основные понятия теории вероятностей
- •1.1 Классификация событий. Действия над событиями
- •1.2. Относительная частота
- •1.3. Классическое определение вероятности
- •1.4. Элементы комбинаторики
- •Примеры решения задач
- •Глава 2. Основные теоремы теории вероятностей
- •2.1 Сложение и умножение вероятностей
- •Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло:
- •Свойства:
- •1. Вероятность произведения n событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
- •2.2 Формула полной вероятности. Формула Байеса
- •Примеры решения задач
- •Глава 3. Повторные испытания
- •3.1 Формула Бернулли
- •3.2 Предельные теоремы Лапласа и Пуассона
- •Примеры решения задач
- •Глава 4. Дискретные случайные величины
- •4.1. Дискретные случайные величины.
- •4.2. Числовые характеристики дискретных случайных величин.
- •1. Математическое ожидание.
- •2. Дисперсия случайной величины.
- •3. Среднее квадратическое (стандартное) отклонение.
- •4. Моменты случайных величин.
- •5. Характеристики формы распределения.
- •4.3. Числовые характеристики меры связи случайных величин.
- •1. Ковариация.
- •2. Корреляция.
- •4.4. Распределения дискретных случайных величин.
- •1. Равномерное распределение.
- •2. Геометрическое распределение.
- •4. Биномиальное распределение.
- •5. Распределение Пуассона.
- •Примеры решения задач
- •Глава 5. Непрерывные случайные величины.
- •5.1. Функция распределения случайной величины
- •5.2. Плотность распределения вероятностей.
- •Связь между функцией распределения и плотностью распределения вероятностей.
- •5.3. Числовые характеристики непрерывных случайных величин
- •Примеры решения задач
- •Глава 6. Распределения непрерывных случайных величин
- •6.1. Равномерное распределение.
- •6.2. Показательное (экспоненциальное) распределение.
- •6.3. Нормальное распределение
- •Примеры решения задач
3. Среднее квадратическое (стандартное) отклонение.
Средним квадратическим отклонением случайной величины X называется арифметический корень из дисперсии:
![]() (4.16)
(4.16)
Из свойств дисперсии вытекают свойства стандартного отклонения.
Свойства стандартного отклонения.
Стандартное отклонение от постоянной величины равно 0:
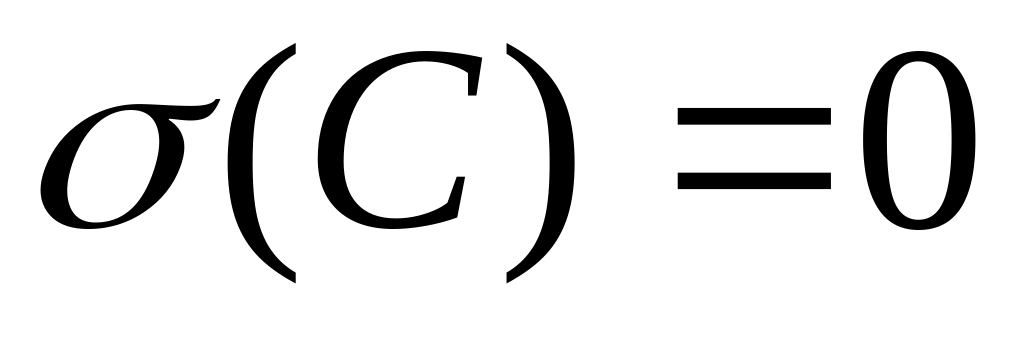 .
.Среднее квадратическое отклонение произведения случайной величины Х на постоянную равно произведению среднеквадратического отклонения случайной величины Х на модуль постоянной:
![]() (4.17)
(4.17)
Если X и Y – независимые случайные величины, то среднее квадратическое отклонение от суммы случайных величин равно:
![]() (4.18)
(4.18)
4. Моменты случайных величин.
Начальным
теоретическим моментом k-ого
порядка
![]() называют математическое ожидание
случайной величины
называют математическое ожидание
случайной величины
![]() :
:
![]() (4.19)
(4.19)
Центральным
теоретическим моментом k-го
порядка
![]() называется математическое ожидание
k-ой степени отклонения
называется математическое ожидание
k-ой степени отклонения
![]() :
:
![]() (4.20)
(4.20)
Если распределение
вероятностей случайной величины
симметрично относительно её математического
ожидания, то все центральные моменты
нечетного порядка равны нулю:![]() .
.
5. Характеристики формы распределения.
Коэффициентом
асимметрии случайной величины Х
называется число
![]() ,
равное отношению третьего центрального
момента к кубу среднеквадратического
отклонения случайной величины Х:
,
равное отношению третьего центрального
момента к кубу среднеквадратического
отклонения случайной величины Х:
![]() (4.21)
(4.21)
Коэффициент асимметрии случайной величины, закон распределения которой симметричен относительно математического ожидания, равен нулю. Если распределение вероятностей несимметрично, причем «длинная часть» распределения расположена справа от центра группирования, то >0, если же «длинная часть» расположена слева, то <0.
Эксцесс Е(Х) – числовая характеристика островершинности закона распределения, равна разности между отношением четвертого центрального момента к среднему квадратическому отклонению в четвертой степени случайной величины Х и цифрой 3:
![]() (4.22)
(4.22)
4.3. Числовые характеристики меры связи случайных величин.
1. Ковариация.
Ковариацией случайных величин X и Y называется число, равное математическому ожиданию произведения отклонений случайных величин X и Y от своих математических ожиданий:
![]() . (4.23)
. (4.23)
Теорема:
Ковариация
независимых случайных величин равна
0:
![]() .
.
Если
![]() ,
случайные величины X
и
Y
зависимы.
,
случайные величины X
и
Y
зависимы.
2. Корреляция.
Корреляцией случайных величин X и Y называется отношение ковариации случайных величин к их средним квадратическим отклонениям:
![]() (4.24)
(4.24)
Для
независимых X
и Y
![]() ,
так как в этом случае cov(X;
Y)=0.
,
так как в этом случае cov(X;
Y)=0.
Свойства коэффициента корреляции.
–1 XY1
Если XY=1, то
 ,
где a
и b—константы,
a>0.
,
где a
и b—константы,
a>0.Если XY= –1, то , где a<0.
Если , (a0) или
 ,
то XY=1
при a>0;
XY= – 1
при a<0.
,
то XY=1
при a>0;
XY= – 1
при a<0.
4.4. Распределения дискретных случайных величин.
1. Равномерное распределение.
Случайная величина Х, принимающая целочисленные значения от 1 до n, имеет равномерное распределение, если
![]() . (4.25)
. (4.25)
Многоугольник
распределения случайной величины Х
представляет
собой отрезок прямой, параллельной оси
абсцисс. Концы отрезка имеют координаты
![]() и
и
![]() .
.
Математическое
ожидание равномерного распределения
![]() .
.
Дисперсия
дискретной случайной величины,
распределенной по равномерному закону
равна
![]() .
.
Стандартное
отклонение
![]() .
.
