Апериодическое звено

Апериодическому звену соответствует дифференциальное уравнение

Tdx_Bых/dt + xвых=kx_BX

Перейдя к изображениям, имеем ТрХ_вых(р) +Х_вых(р) =kX_BX(p). Передаточная функция звена

W(p)=K/(Tp+1)

Кривые переходных процессов имеют вид экспонент, т. е. время, необходимое для того, чтобы выходная величина х_вых достигла ус­тановившегося значения х_0вых, теоретически бесконечно велико. В связи с этим апериодическое звено часто называют инерционным звеном первого порядка.

Величина Т имеет размерность времени и называется постоянной времени звена. Постоянная времени определяет дина­мические свойства звена. Чем она больше, тем медленнее протекает переходный процесс в звене, и наоборот. В частности, при Т=0 про­цесс протекает в звене мгновенно и инерционное звено превращает­ся в безынерционные усилительное. Следует отметить также, что при t=T значение выходной величины составляет 63% нового устано­вившегося значения.

Графическое определение постоянной времени апериодического звена

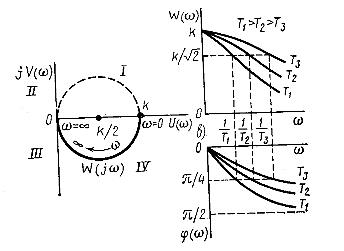
Рисунок 1.8 – Частотные характеристики апериодического звена

Рисунок 1.9– Графическое определение постоянной времени апериодического звена

Колебательное звено

Передаточная функция колебательного звена

W(p)=k/(Tp²+T₁p+1)

Характер переходного процесса звена или соединения, определя­емого дифференциальным уравнением , зависит от располо­жения корней его характеристического уравнения Tp²+Tp+1=0

Передаточная функция и переходные процессы колебательного звена при различных значениях отношения постоянных времени.

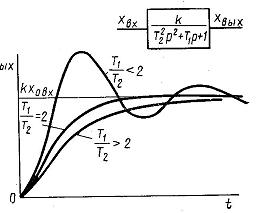
Рисунок 1.10 – Передаточная функция и переходные процессы колебательного звена при различных значениях отношения постоянной времени

Рисунок 1.11 - Комплексные частотные характеристики колебательного звена

Рисунок 1.12 - Амплитудно-частотные и фазочастотные характеристики колебательного звена

Форсирующее звено

Форсирующим называется звено, дифференциальное уравнение которого имеет вид:

его можно представить как сумму пропорционального и дифференцирующего звеньев.

Передаточная функция форсирующего звена,

Записывается в стандартной формуле:

где – коэффициент передачи, – постоянная времени звена.

Определим теперь его переходную характеристику:

h

τ t

Рисунок 1.13 - Переходная характеристика форсирующего звена

Выражения для частотных характеристик:

АФХ:

ВЧХ:

МЧХ:

АЧХ:

ФЧХ:

I

ω ∞

ω 0

R

Рисунок 1.14 – АФХ форсирующего звена