Дифференцирующие звено

Д уравнением

Передаточная функция звена:

Выходная величина дифференцирующего звена пропорциональна производной по времени от входной величины. Коэффициент пропорциональности k называется коэффициентом усиления или коэффициент передачи звена.

Если выходная и входная величина имеют одинаковую размерность, то коэффициент k выражается в секундах, тогда его обозначают T [c]-постоянная времени дифференцирующего звена.

Частотные характеристики:

,

,

,

,

Рисунок 1.1 - Амплитудно-фазовая характеристика

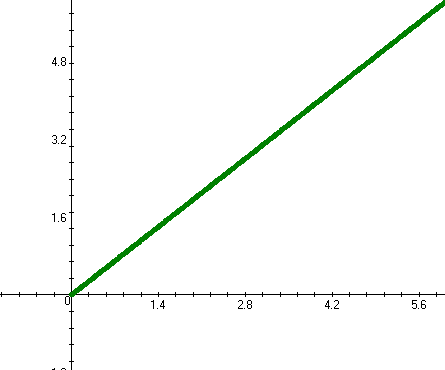
Рисунок 1.2 - Амплитудно-частотная характеристика

Рисунок 1.3 – Фазо-частотная характеристика

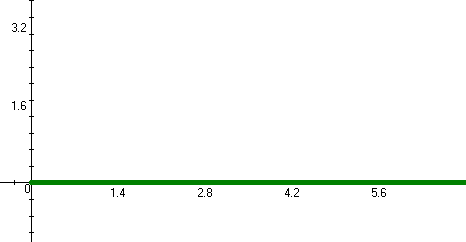
Рисунок 1.4 – Вещественно-частотная характеристика

Усилительное звено

В усилительном звене выходная величина в каждый момент времени пропорциональна входной величине, т. е. х_вых = кх_вх Здесь и в дальнейшем для сокращения записи выражения х_вых(t) и х_BX(t) представ­ляем как х_вых и х_вх. Пе­реходные процессы рас­сматриваются при нуле­вых начальных условиях. Коэффициент пропорцио­нальности k называют ко­эффициентом усиления или коэффициентом передачи звена. Уравнение усилительного звена алгебраическое. Это сви­детельствует о том, что усилительное звено передает сигнал мгновенно, без динамических переходных процессов и искажений.

На рисунке представлен характер изменения по времени выходной величины усилительного звена при подаче на его вход постоян­ной входной величины х_0вх.

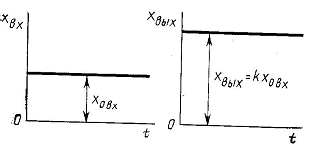
Рисунок 1.5 – Передаточная функция и временная характеристика усилительного звена

Передаточная функция звена имеет вид

W(p) = k

Примерами усилительных звеньев могут служить механические передачи, потенциометрические датчики, безынерционные усилите­ли (например, электронные) и т. п.

Таким образом, КЧХ усилительного звена представляет вектор, совпадающий с положительным направлением оси абсцисс, модуль которого не зависит от частоты и равен коэффициенту передачи звена.

Воздействия любой частоты, поступающие на вход этого звена, усиливаются в одинаковой степени без фазового сдвига. Усилительное (безъинерционное, пропорциональное):механические передачи, потенциометрические датчики, электрические усилители, делитель напряжения, трансформатор.

Интегрирующее звено

Выходная величина интегрирующего звена пропорциональна интегралу входной величины, т. е.

х_вых=k§x_вхdt

Дифференциальное уравнение интегрирующего звена имеет вид

dx_вых/dt = kx_Bх

Коэффициент k называют коэффициентом усиления звена по скорости. Он численно равен скорости изменения выходной величины при единичном значении входной величины.

Рисунок 1.6 – Передаточная функция и временная характеристика интегрирующего звена

Преобразовав дифферен­циальное уравнение звена по Лапласу, получим рХ_вых (р)= kх_вх (p), откуда находим передаточную функцию звена:

W(p)=k/p

Если входная и выходная величины имеют одинаковую размер­ность, то следует, что коэффициент k имеет размерность с^-1. В этом случае дифференциальное уравнение удобнее представить в виде

dx^вых/dt = х_вх/Т

где Т= 1/k.

Рисунок 1.7 – Частотные характеристики интегрирующего звена

При этом передаточная функция звена примет вид

W(p)=1/Tp

Величину Т называют постоянной времени интегрирующего звена звена.

На рисунке представлен характер изменения выходной величины интегрирующего звена при подаче на его вход постоянной входной величины х₀вх.