
- •6 Цепи с распределёнными параметрами
- •6.1.2 Решение телеграфных уравнений для линии с потерями
- •6.2 Коэффициент отражения
- •6.3 Режим бегущих волн
- •6.4 Режим стоячих волн
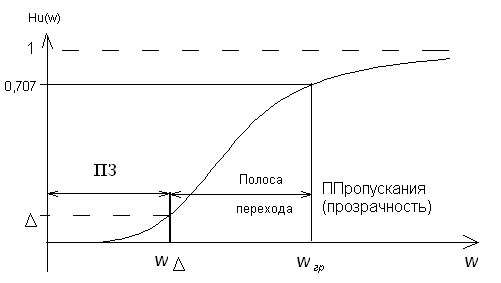
- •6.4.1 Разомкнутая линия
- •6.4.2 Входное сопротивление линии при холостом ходе
- •6.4.3 Короткозамкнутая линия
- •6.5 Применение длинных линий
- •6.5.2 Согласование линии с нагрузкой при помощи четвертьволнового трансформатора
- •6.5.3 Согласование с помощью шлейфа Татаринова
- •6.5.4 Линия как колебательная система
- •Электрические фильтры .
- •1 Виды фильтров.
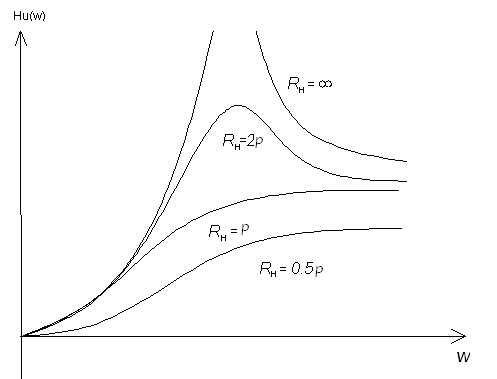
- •Передаточная функция фильтра
- •2.1 Определить комплексную передаточную функцю фильтра низких частот
- •2.2) Фвч ― фильтр верхних частот.
- •Схемы пассивных lc-фильтров.
- •3.2) Фильтр верхних частот (фвч).
- •3.3) Полосовой фильтр
- •1 Уравнения и параметры чп
- •2 Входное и выходное сопротивления чп
- •3 Характеристические параметры чп
- •3.1 Характеристические сопротивления (формулы исправить)
- •3.3 Характеристическая постоянная передачи
- •3.4 Передаточная функция
Передаточная функция фильтра
Нu(j
)= .
.
Представленные выше звенья являются звеньями второго порядка. Комплексная передаточная функция (КПФ) такого звена имеет вид:
Нu(j
)=
Здесь
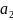 ,
, ,
,
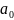 ( т.е.
( т.е.
 при
при
 =
= )
и
)
и
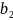 ,
,
 ,
,
 (т.е.
(т.е.
 при
при
 )
― действительные
(вещественные) положительные величины
при разных степенях аргумента
)
― действительные
(вещественные) положительные величины
при разных степенях аргумента
 .
.
Максимальная степень аргумента определяет порядок звена ( звено 2-го порядка ).
Степень
числителя не может быть выше степени
знаменателя. Некоторые коэффициенты
могут быть нулевыми. В отличии от
числителя все коэффициенты знаменателя
ненулевые
 0.
Степень полинома знаменателя равна 2
при наличии в схеме как минимум, двух
реактивных элементов с разным характером
реактивности. Коэффициенты
и
комплексной передаточной функции КПФ
определяются значениями L
и C
и структурой фильтра.
0.
Степень полинома знаменателя равна 2
при наличии в схеме как минимум, двух
реактивных элементов с разным характером
реактивности. Коэффициенты
и
комплексной передаточной функции КПФ
определяются значениями L
и C
и структурой фильтра.
2.1 Определить комплексную передаточную функцю фильтра низких частот
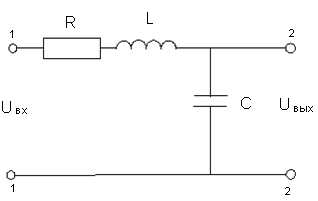
Нu(j )= .
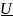 вых=
вых= );
вх=
);
вх=

Значение КПФ принимает вид:
Нu(j
)= =
=
В этом выражении КПФ В числителе а2=а1=0; а0=1; в знаменателе =LC; =RC; =1.
Таким образом, звено второго порядка является фильтром низких частот при условии а2=а1=0:
Нu(j
)=
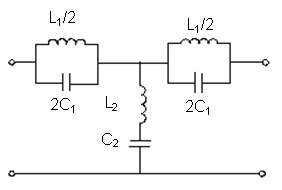
Тогда АЧХ ФНЧ определяется выражением | Нu(j )|
Нu(
)=
С помощью этого выражения можно рассчитать коэффициент передачи на любой частоте.
Значение
Нu(
)
на нулевой частоте Нu(
=0)= =1
=1
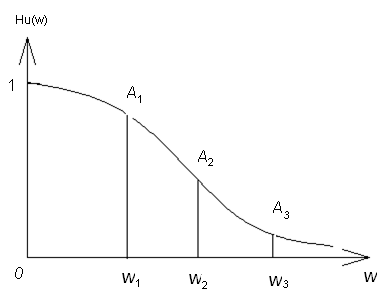
H( )=Н1
;
H(
)=Н1
;
H( )=H2
H(
)=H2
H(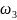 )=H3
)=H3
Нu(j
)=
2.2) Фвч ― фильтр верхних частот.
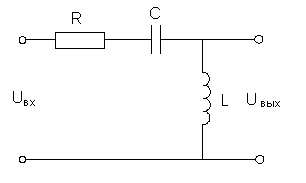
Нu(j
)=
=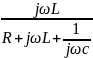 =
=
или
Нu(j
)= .
.
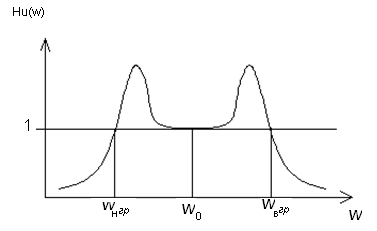
AЧХ описывается выражением
Нu(
)= .
.
При

Нu( =
= =
= =1
=1
2.3) Для произвольного фильтра в виде звена n-го порядка КПФ имеет следующий вид:
 j
j =
=
Причем n ≥ m.
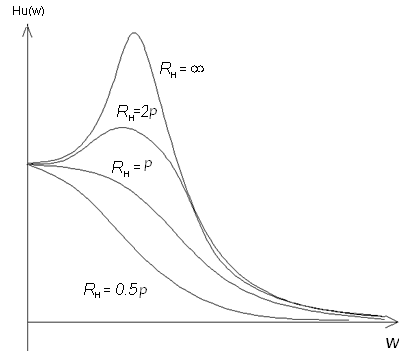
В
зависимости от того, какие из коэффициентов
равны нулю, модуль КПФ
 по разному зависит от частоты на разных
участках частотного диапазона. Формируют
АЧХ различного вида, которые соответствуют
различным видом фильтров.
по разному зависит от частоты на разных
участках частотного диапазона. Формируют
АЧХ различного вида, которые соответствуют
различным видом фильтров.
Схемы пассивных lc-фильтров.
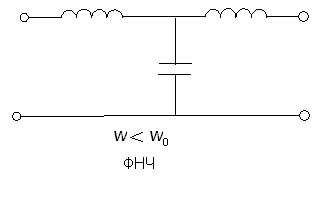
3.1) ФНЧ
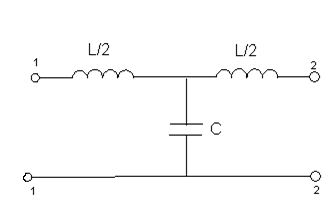
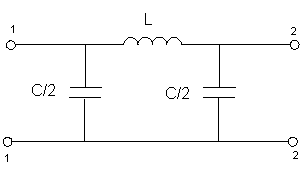
Т-образная схема П-образная схема
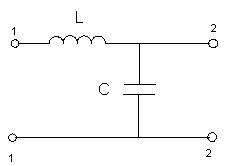
Г-образная
 ;
;
C=
;
;
C= ;
L=
;
L=
Для
расчета параметров фильтра заданным
являются граничная частота
 и сопротивление нагрузки. Наилучших
частотных свойств можно застичь в режиме
согласования. Приближение к этому режиму
и сопротивление нагрузки. Наилучших
частотных свойств можно застичь в режиме
согласования. Приближение к этому режиму
 .
.
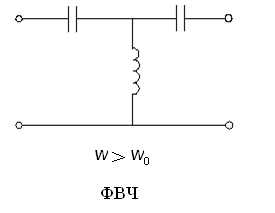
3.2) Фильтр верхних частот (фвч).
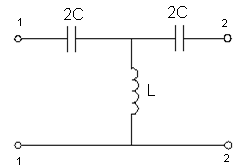
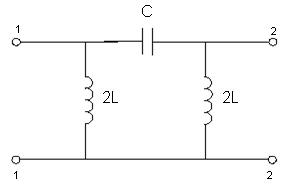
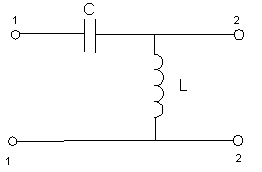
 ;
;
 C=
C= ;
L=
;
L= .
.
3.3) Полосовой фильтр
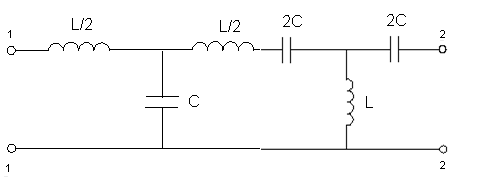
Каскадные соединение ФНЧ и ФВЧ
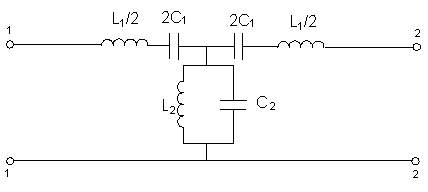
Более практична в настройке последовательном и параллельном КК настроено на одну частоту.
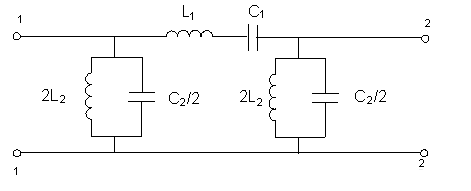
П-образная схема.
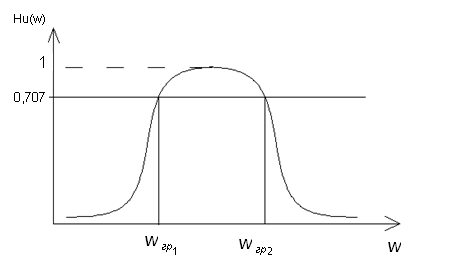
Комплексное
сопротивление последовательного
идеального колебательного контура,
который включается в продольную ветвь
 ,
на частоте
,
на частоте
 ;
;
 ;
а параллельного, который включается в
поперечную ветвь
;
а параллельного, который включается в
поперечную ветвь
 .
.
Эквивалентные схемы полосового Т-образного фильтра имеют следующий вид :
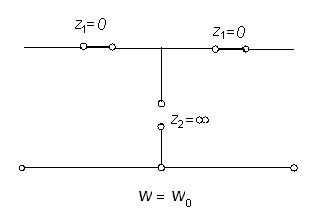
На
частотах
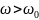 последовательные контуры ведут себя
как индуктивное сопротивление, а
параллельного контура, как емкостное
сопротивление. Эквивалентная схема
приобретает вид рис.2. Она подобна ФНЧ.
последовательные контуры ведут себя
как индуктивное сопротивление, а
параллельного контура, как емкостное
сопротивление. Эквивалентная схема
приобретает вид рис.2. Она подобна ФНЧ.
При
частоте ниже резонансной ( )
последовательные ветви ведут себя
емкостные, а параллельные ― как
индуктивные. Эквивалентная схема ФВЧ
. Для расчета задают
)
последовательные ветви ведут себя
емкостные, а параллельные ― как
индуктивные. Эквивалентная схема ФВЧ
. Для расчета задают
 :
:
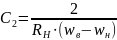 ;
;
 ;
;
 ;
;
 .
ZZZ///
.
ZZZ///
ЧЕТЫРЁХПОЛЮСНИКИ
Ч етырёхполюсником
называется часть электрической цепи,
имеющей два входных и два выходных
зажима. К входным зажимам присоединяется
источник, а к выходным – приёмник
энергии. Примерами четырёх-полюсников
(ЧП)
является усилитель,
етырёхполюсником
называется часть электрической цепи,
имеющей два входных и два выходных
зажима. К входным зажимам присоединяется
источник, а к выходным – приёмник
энергии. Примерами четырёх-полюсников
(ЧП)
является усилитель,
Рисунок 1-Схемное обозначение ЧП
трансформатор, электрический фильтр, линия связи и т.д. Эти устройства, не похожие по внутреннему содержанию, можно описать общим набором параметров ЧП.
Ч
1′
R
етырёхполюсники могут быть пассивные и активные, линейные и нелинейные, симметричные и несимметричные.ЧП называется симметричным, если при взаимной замене первичных 1-1′ и вторичных 2-2′ выводов токи и напряжение на входе и выходе ЧП не поменяются.
Режим работы ЧП
полностью
определён, если известны
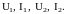 Основной задачей теории ЧП
является установление соотношений
между этими величинами. Уравнения,
которые дают зависимость между
Основной задачей теории ЧП
является установление соотношений
между этими величинами. Уравнения,
которые дают зависимость между
 называются уравнениями передачи
четырёхполюсника
называются уравнениями передачи
четырёхполюсника
