6.3 Режим бегущих волн

Этот режим может быть получен, если линия нагружена на сопротивле­ние z_н=z₀ : отраженные волны отсутствуют, есть только падающая или бегущая волна.

Характер изменения амплитуды напряжения и тока вдоль линии в режиме бегущих волн определяется выражениями (6.18) и (6.19),

полученными для прямой волны линии с потерям:

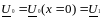
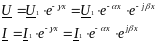
Видно, что амплитуды напряжения и тока убывают по экспоненциальному

закону 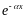, а начальные фазы колебаний изменяются линейно

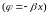
Входное сопротивление линии в режиме бегущих волн равно волновому сопротивлению.

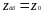
Мгновенные значения напряжения и тока равны:

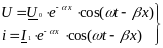(6.25)

Мгновенное значение мощности, передаваемой по линии р =U • i или

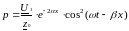(6.26)

Видно, что при любом t и при х <= I всегда р => 0 , то есть мощность передается от генератора к нагрузке, часть мощности теряется в нагрузке.

6.4 Режим стоячих волн

Если прямая волна встречает на своем пути электрическую неоднород­ность, то в линии возникают обратные или отраженные волны. Отражения возникают:

1. В точке соединения двух отрезков линии с различными параметрами

2. На конце линии, нагруженной на сопротивление, не равное волновому При сложении падающей и отраженной волн равных амплитуд в линии устанавливается режим стоячих волн (линии без потерь).

Для полного отражения падающей волны необходимо, чтобы нагрузка не потребляла энергию. Это возможно при:

а) линия, разомкнутая на конце (z_H = z₂ = °°);

б) линия, замкнутая на конце (z₂ = О );

в) линия, нагруженная на реактивное сопротивление ( )

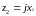6.4.1 Разомкнутая линия

В режиме холостого хода

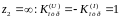
В разомкнутой линии падающая и отраженная волны имеют одинаковые амплитуды колебаний, причем напряжение падающей и отраженной волн совпадают по фазе, а токи сдвинуты на 180 градусов. Поэтому напряжение в точке отражения достигает максимума (увеличение в два раза), а ток равен нулю.

Найдем комплексные амплитуды напряжения и тока в линии. Для линии без потерь:

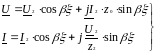(6.27)

Где ξ - расстояние от конца линии до рассматриваемой точки линии. При ξ= 0 (на конце линии) 1₂ = 0 (режим холостого хода).

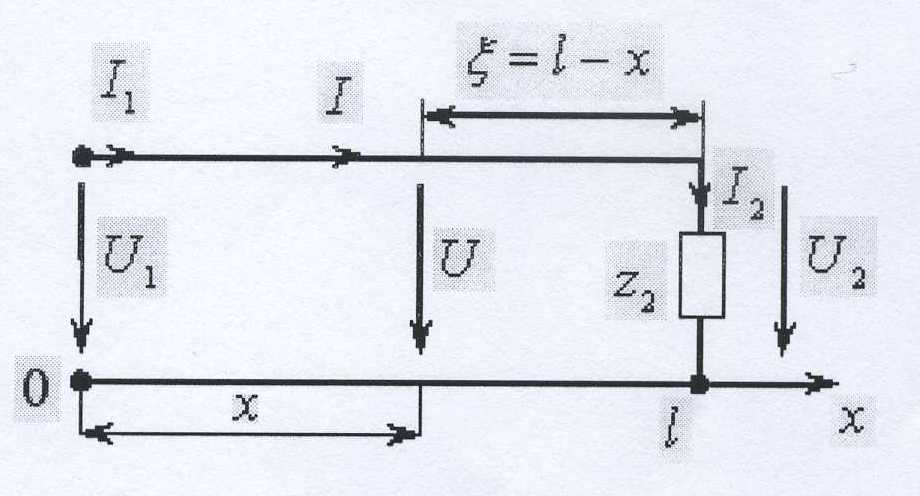
В общем случае с произвольной нагрузкой z₂

Тогда комплексные амплитуды вдоль линии изменяются по закону:

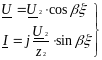(6.28)

Мгновенные значения тока и напряжения в линии имеют вид:

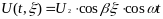
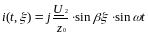
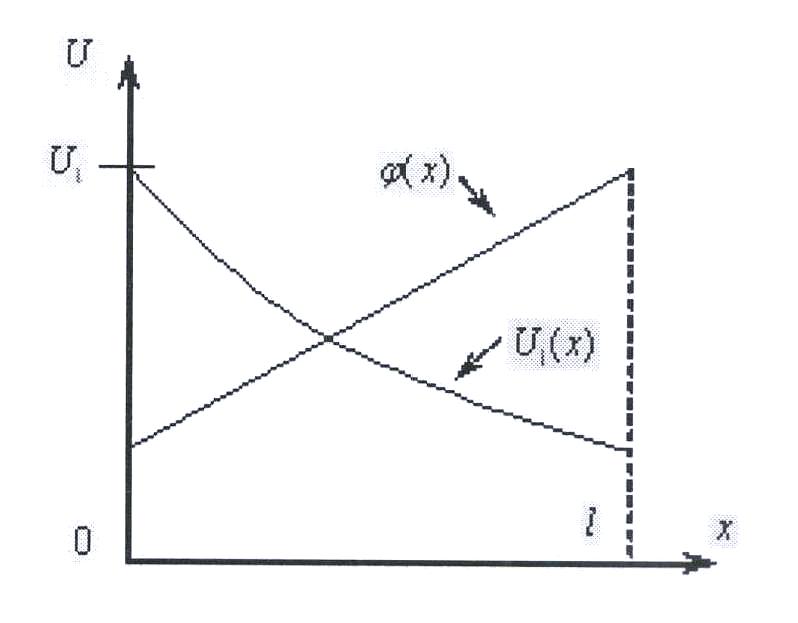
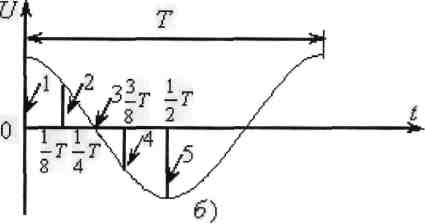
Графики пространственного изменения напряжения (вдоль линии) представлены на рисунке: U = f(x) . Каждая из кривых соответствует своему мгновенному значению.(Рисунок б)

£ = 0

х=1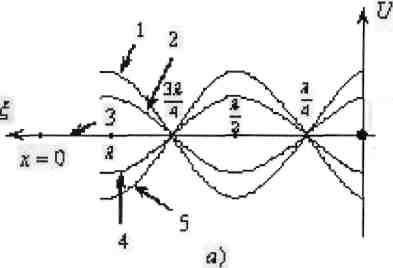

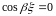Из рисунка (а) видно, что напряжение в отдельных точках линии равно нулю. Эти точки называются узлами напряжения. Положение узлов определяется из условия , откуда 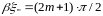или 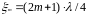, где ξ_т - координата т - го узла.

В конце линии и между узлами расположены точки, где амплитуды напряжения имеют максимальные значения. Эти точки называются

пучностями напряжения. Их координаты 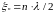, где п - 0,1,2,3... Аналогичный вид имеют распределение тока вдоль линии, однако они сдвинуты относительно напряжения на λ/4 ; (рисунок)

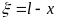
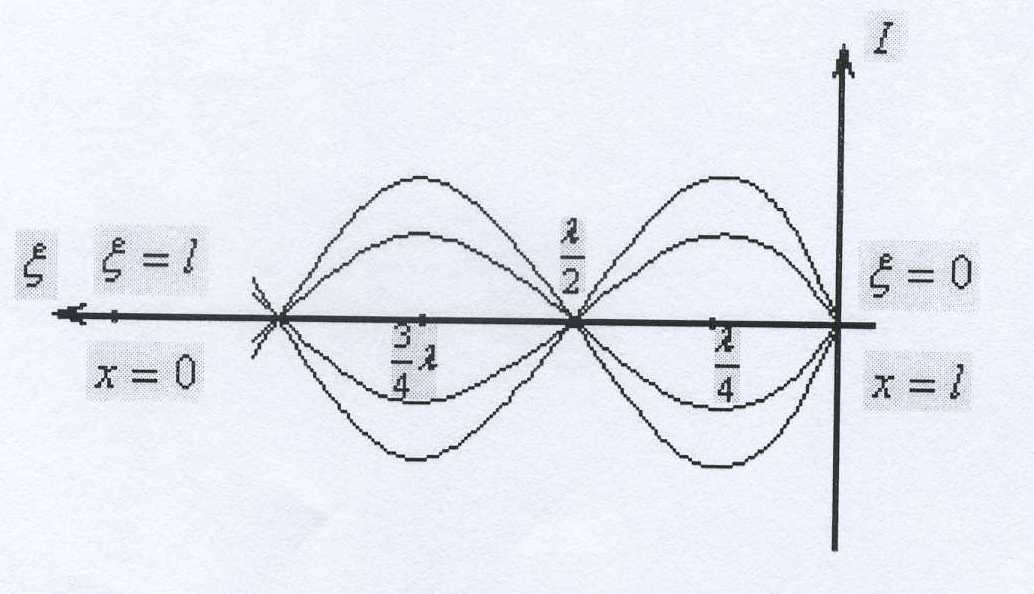
Пучности напряжения (или тока) имеют место в тех точках линии, где напряжения (или токи) падающей и отраженной волн имеют одинаковые фазы, а узлы - в точках, где эти волны находятся в противофазе.