6.1.2 Решение телеграфных уравнений для линии с потерями

На входе длинной линии действует гармоническая ЭДС. В этом случае для мгновенных значений комплексных величин напряжения и тока запишем:

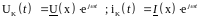
где U(x), I(x) - комплексные амплитуды напряжения и тока.

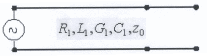
Телеграфные уравнения (6.1) для комплексных амплитуд запишем так:

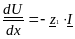
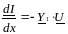(6.12)

где z₁=R₁+jωL₁ - полное сопротивление линии на единицу длины. Y₁=G+jωC₁ - полная проводимость линии на единицу длины. Продифференцируем по X уравнения (6.12), получим:

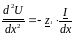
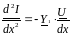(6.13)

(6.13) Подставляя в уравнения (6.13) значения производных из (6.12), получим:

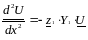
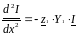(6.14)

Решение дифференциального уравнения второго порядка для комплексной амплитуды напряжения имеет вид:

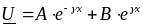
(6.15)

Здесь А и В - постоянные коэффициенты интегрирования.

γ =α+ jβ - постоянная распространения, которая является комплексной величиной, где а - коэффициент затухания; J3 - коэффициент фазы.

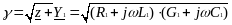(6.16)

В линии без потерь

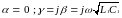
Ток в линии

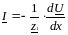
Так как

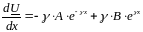
То 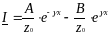(6.17)

Здесь 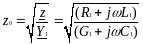волновое сопротивление линии с потерями.

Для линии без потерь: R=0; G=0;

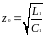
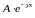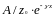В выражениях (6.15) и (6.17) первые слагаемые и определяют комплексные амплитуды напряжения и тока прямой

волны, вторые слагаемые - комплексные амплитуды напряжения и тока отраженной волны.

Выясним физический смысл коэффициентов α и β. Для этого рассмотрим выражение для напряжения и тока прямой волны:

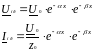(6.18)

где U₀ = А - комплексная амплитуда напряжения прямой волны в начале линии при х = О. Мгновенное значение напряжения:

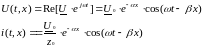(6.19)

х=0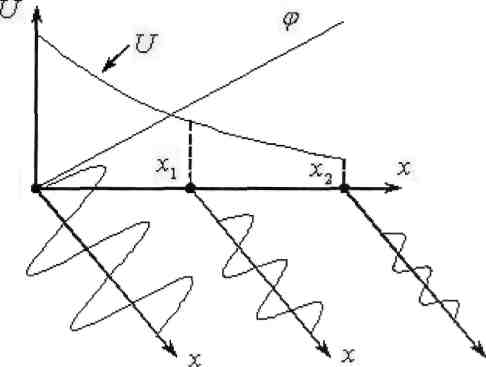

Таким образом, распространение волны вдоль линии с потерями сопровождается затуханием амплитуды по экспоненте e^-αx и изменением фазы (-βx).

6.2 Коэффициент отражения

Определим значение прямой и отраженной волны в линии с потерями, что даст возможность проанализировать условия возникновения отражений в данной линии.

Решения дифференциального уравнения второго порядка для U и I содержат коэффициенты интегрирования А и В. Определим эти коэффициенты из граничных условий.

Пусть линия длиной / нагружена на сопротивление нагрузки Z ₂ . Тогда граничные условия принимают вид:

при х=l:

известны z₂, U₂,

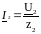
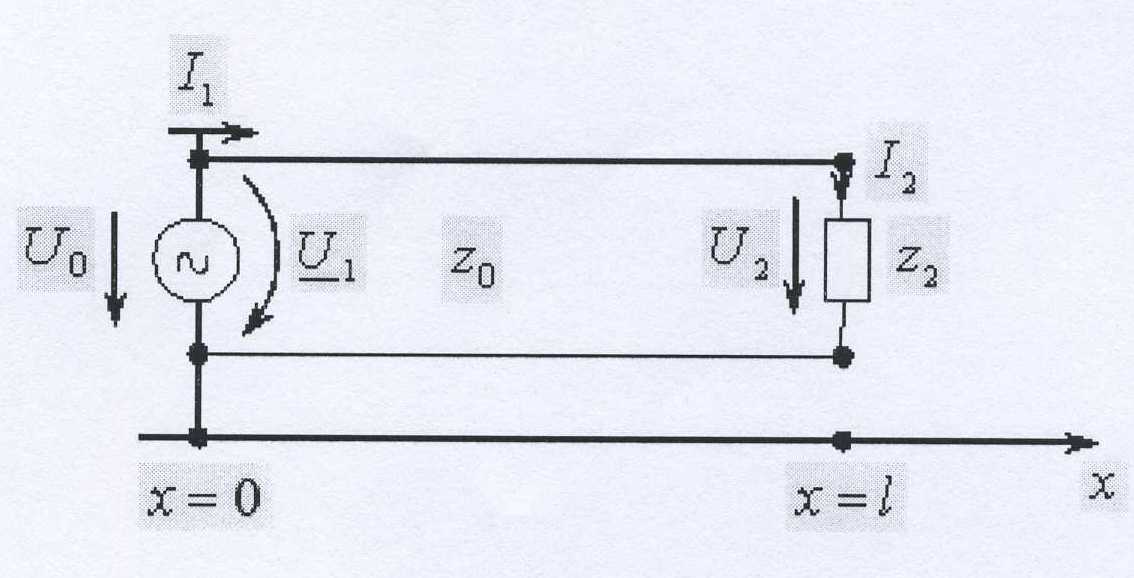
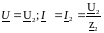
Применив эти условия к решению дифференциальных уравнений (6.15) и (6.17), будем иметь: (при х = l)

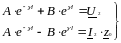(6.20)

Для получения А сложим эти уравнения:

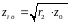
Для получения В из первого вычтем второе:

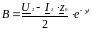
Из решения данной системы уравнений находим:

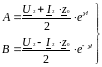(6.21)

Подставляя А и В в исходные решения (6.15) и (6.17), получим выражения для расчета напряжения и тока в любой точке линии:

U_пр=A-e^-γx U_отр=B-e^-γx

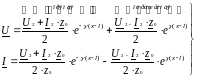(6.22)

Первые слагаемые - комплексные амплитуды напряжения и тока падающей (прямой) волны, а вторые слагаемые - обратной или отраженной волны.

Прямая или падающая волна распространяется от генератора к нагрузке, а отраженная - от нагрузки к генератору.

Отношение комплексной амплитуды напряжения отраженной волны к комплексной амплитуде падающей волны в точке х = I называется коэффициентом отражения:

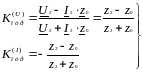(6.23)

Величина коэффициентом отражения зависит от соотношения между сопротивлением нагрузки и волновым сопротивлением.

Рассмотрим значения коэффициентом отражения в зависимости от величины и характера нагрузки.

1) При сопротивлении нагрузки, равном волновому сопротивлению z ₂ = z₀ :

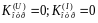
Следовательно, если к отрезку длинной линии подключено сопротивле­ние, равное волновому, то он ведет себя как бесконечно длинная линия - в линии отсутствуют отраженные волны.

2) Нагрузка является реактивной: 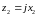. В этом случае коэффициентом отражения равен:

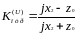
Модуль коэффициента отражения волны напряжения и тока равен еди­нице, то есть при чисто реактивной нагрузке любой величины падающая волна полностью отражается.

3) Линия, разомкнутая на конце ( Z₂ = °° ).

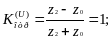
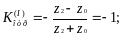
Следовательно, от разомкнутого конца линии волна напряжения полностью отражается с тем же знаком, а волна тока отражается с противоположным знаком. Напряжение на конце линии удваивается, а ток на конце линии равен нулю.

4) Линия, замкнутая на конце. В этом случае z₂ = 0 .

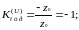
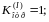
Следовательно, от замкнутого конца линии волна напряжения полностью отражается с противоположным знаком. В результате напряжение на конце линии равно нулю, а ток - удваивается.