Преобразование нелинейной цепью суммы двух гармонических колебаний
Свойство нелинейной цепи обогащать спектр входного сигнала наиболее ярко проявляется при воздействие на нее суммы нескольких гармонических колебаний с различными частотами. Рассмотрим простейший случай, когда вольт-амперная характеристика нелинейного элемента в окрестностях рабочей точки описывается полиномом второй степени:
(6. 14)
На вход этого элемента полается бигармоническое колебание вида
. (6. 15)
Ток через нелинейный элемент определим, подставляя (6. 15) в (6. 14):
Использую тригонометрические формулы:
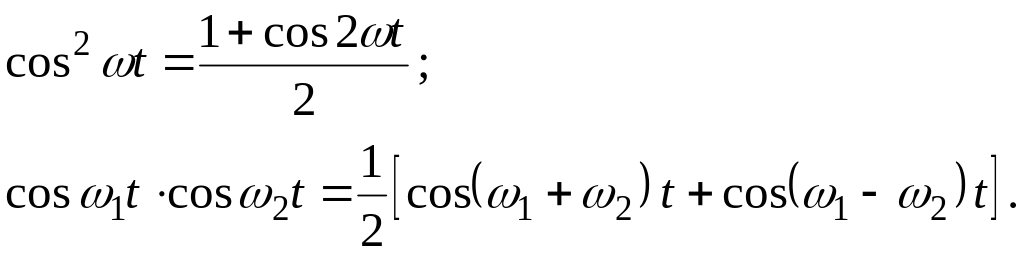
получим значения
тока в следующим виде: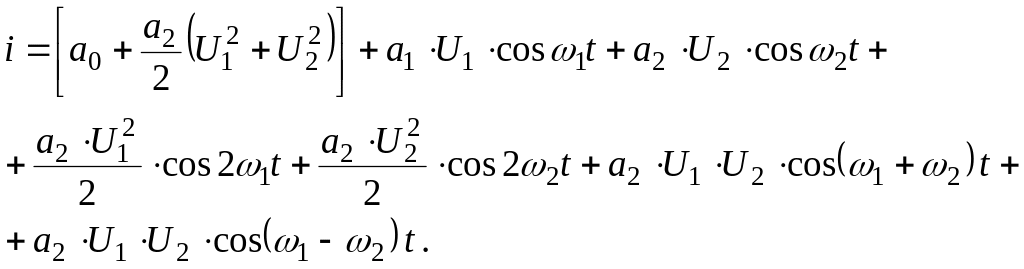 
(6. 16)
Спектральная диаграмма тока в соответствие с (6. 16) показана на рисунке 6.10.
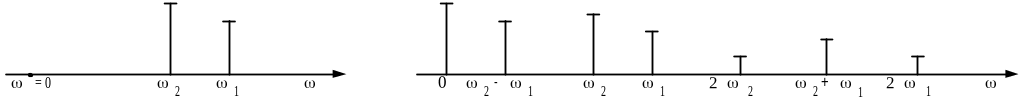
Рисунок 6. 10
Принципиально
новым результатом по сравнению с
воздействием на нелинейный элемент
одного гармонического колебания является
появление спектральных составляющих
с частотами
и
,
которые называются комбинационными
частотами.
В более общем случае ВАХ нелинейного элемента аппроксимируется полиномом n-ой степени в соответствие с выражением
(6. 17)
Подставляя значение бигармонического сигнала (6. 15) в (6. 7) , получим:
(6. 18)
Чтобы найти
спектральный состав тока в соответствии
с (6. 18) надо для каждого значения
составить развернутое выражение k-ой
составляющей
,
выразив его слагаемые через гармонические
функции. Расчеты показывают, что
составляющие высших степеней приводят
к появлению колебаний кратных частот
и
,
а также комбинационных частот вида
где m и n –– целые положительные числа, значения которых определяются видом ВАХ нелинейного элемента.
Эффект обогащения спектра нелинейным элементом при воздействие на него суммы гармонических колебаний лежит в основе работе многих радиотехнических устройств.