6. 4 Преобразование гармонического сигнала в нелинейной цепи

На нелинейное сопротивление с ВАХ подается напряжение сигнала , спектр которого известен. Определить спектральный состав тока , протекающего в цепи с нелинейным элементом (Н. Э.). Пусть в цепь включено также постоянное смещение (рисунок 6. 7, а). Вследствие нелинейности вольт-амперной характеристики форма тока будет отличаться от гармонической. Представим периодическую функцию в виде ряда Фурье:

где –– постоянная составляющая тока;

–– амплитуды гармоник;

–– фаза гармоник.

Ток, протекающий через цепь с нелинейным элементом, содержит высокочастотные составляющие, которые являются следствием проявления нелинейности. Если бы вольт-амперная характеристика была линейна, то высших гармоник (при ) не было бы. Таким образом, нелинейные элементы обладают свойством преобразования частоты входного сигнала, которое заключается в том, что в нелинейных устройствах спектр выходного сигнала содержит новые гармоники, которых нет у входного сигнала (воздействия).

Расчет составляющих тока при заданных амплитуде напряжения U и напряжения смещения можно выполнить различными методами. Рассмотрим два из них:

1) метод степенного полинома;

2) метод кусочно-линейной аппроксимации.

а)

б)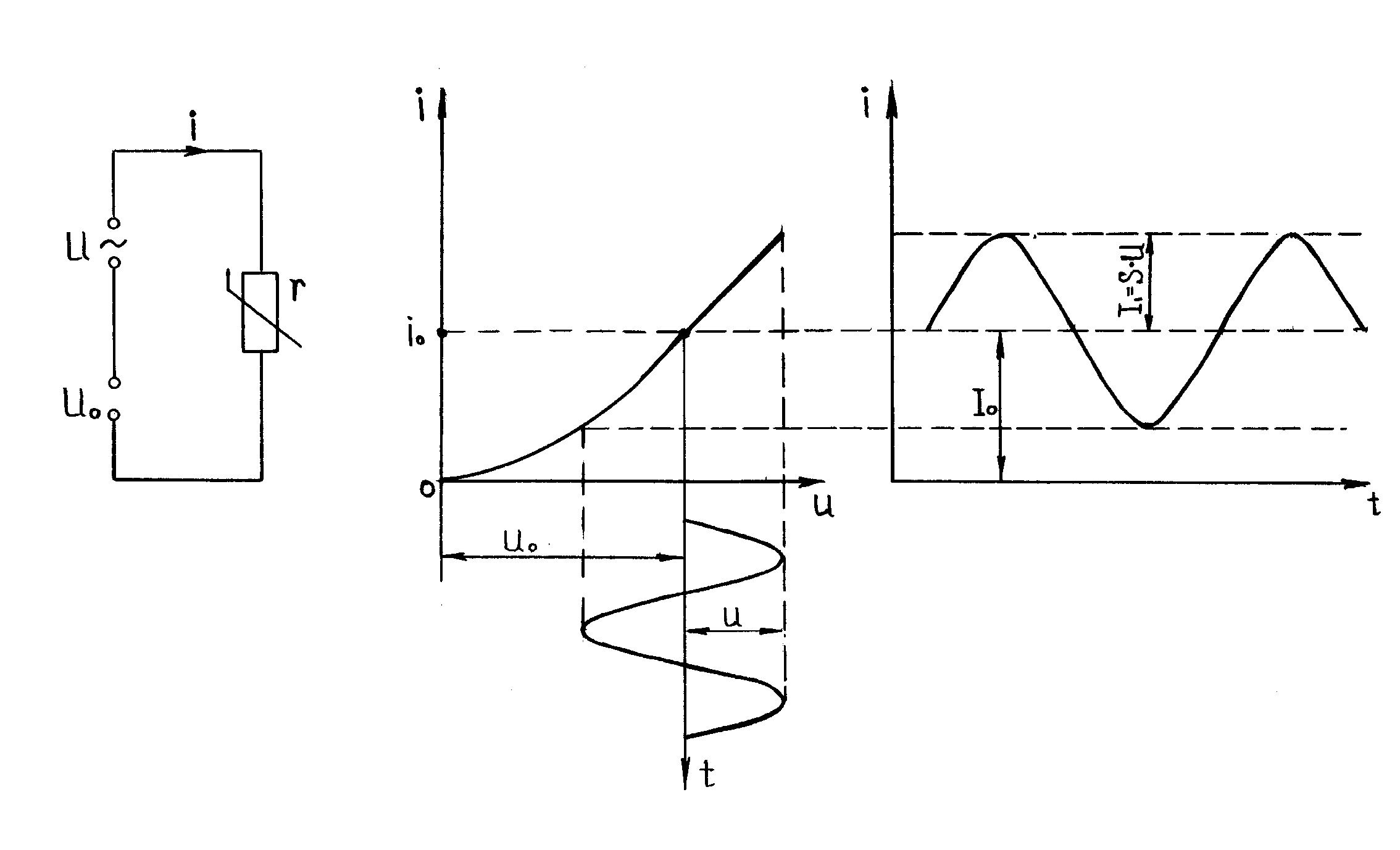

в)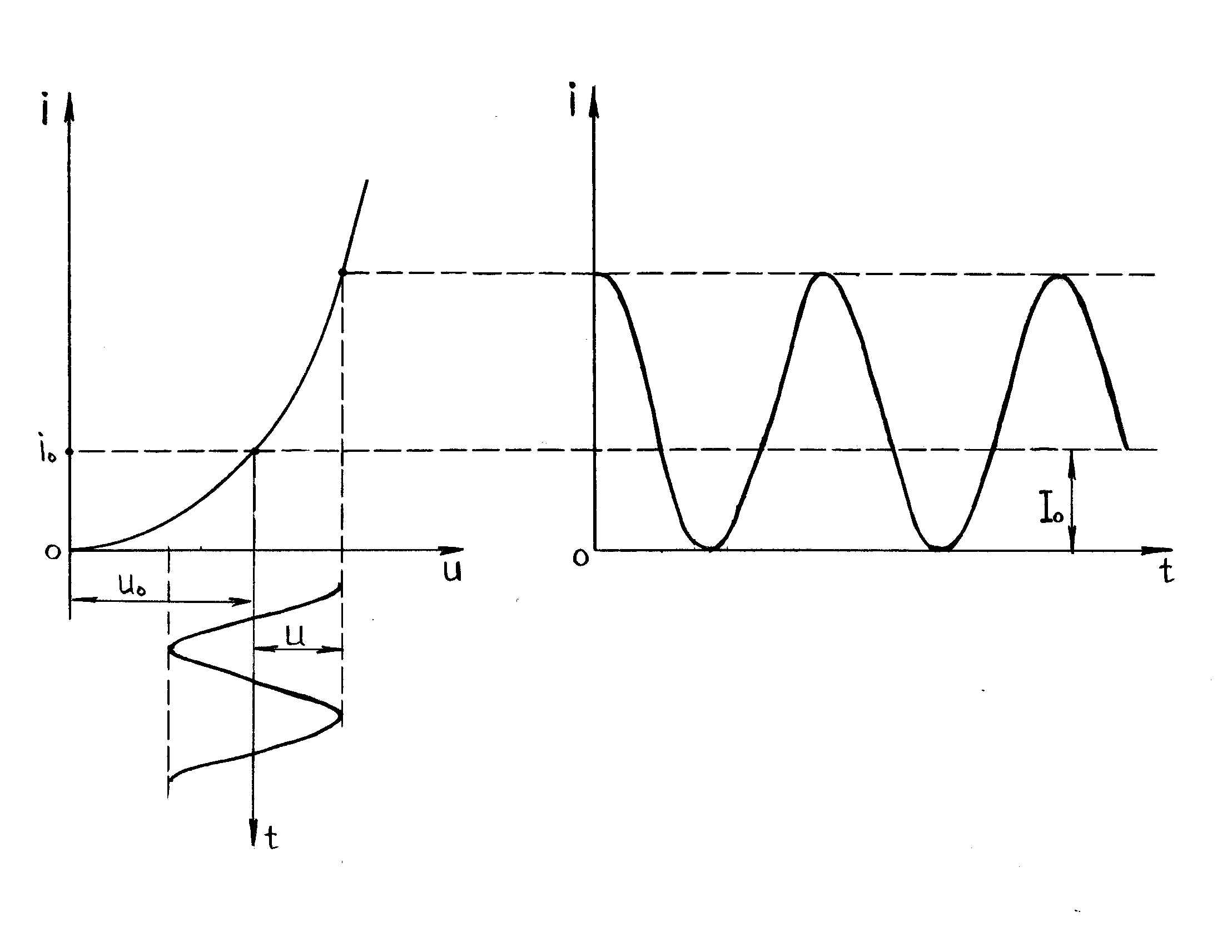

Рисунок 6. 7

Расчет составляющих тока при заданных амплитудах напряжения U и напряжения смещения можно выполнить различными методами. Рассмотрим два из них:

1) метод степенного полинома;

2) метод кусочно-линейной аппроксимации.

6. 4. 1 Исследование нелинейной цепи методом степенного полинома

Известно, что ВАХ нелинейного элемента может быть аппроксимирована степенным полиномом: , или при

В нашем случае .

Выполняя разложение для окрестности точки , получим уравнение для вольт-амперной характеристики в виде:

, (6. 6)

где –– ток покоя;

–– крутизна в исходной точке.

Так как , то

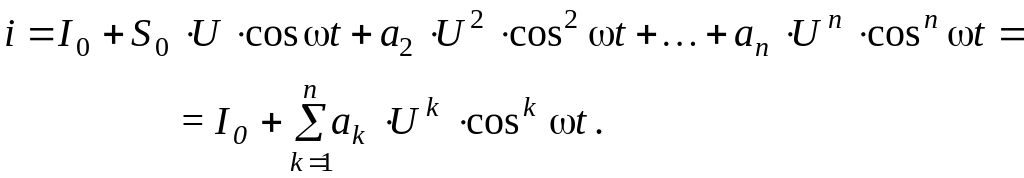(6. 7)

Рассмотрим 2 типичных случая: режим малого и режим большого сигнала.

1. Режим малого сигнала

Вольт-амперная характеристика нелинейного элемента и характер изменения тока в цепи приведены на рисунке 6.7.б.

При этом переменное напряжения сигнала на входе мало и рабочий участок характеристики можно принять за отрезок прямой линии. Членами высших порядков полинома (6.7)можно пренебречь. В этом случае выходная функция (ток) содержит постоянную составляющую и первую гармонику :

— постоянная составляющая тока,

— сопротивления постоянному току.

Амплитуда тока основной частоты

здесь –– сопротивление переменному току в рабочей точке или дифференциальное сопротивление.

Итак, в режиме малых колебаний рабочий участок остается в пределах линейной части характеристик, и от смещения не зависит.

2. Режим большого сигнала

Амплитуда переменного напряжения настолько велика, что рабочий участок выходит за пределы линейного участка вольт-амперной характеристики. Форма тока отличается от косинусоиды. В этих условиях пренебрегать членами высших степеней ряда (6.7) нельзя, так как эти высшие составляющие и будут определять тот эффект, который дает нелинейность. Продукты нелинейности количественно определяются членами полинома (6.7) при .

Составим таблицу составляющих ряда (6. 7) при различных k.

Таблица 6. 1

k		Частота
0		0
1
2
3
4

Видно, что члены четных степеней ряда дают слагаемые четных гармоник, а члены нечетных степеней приводят к появлению составляющих всех нечетных гармоник. Из этого следует:

1. Нелинейность цепи приводит к тому, что спектр тока в общем случае содержит постоянную составляющую и гармоники с частотами 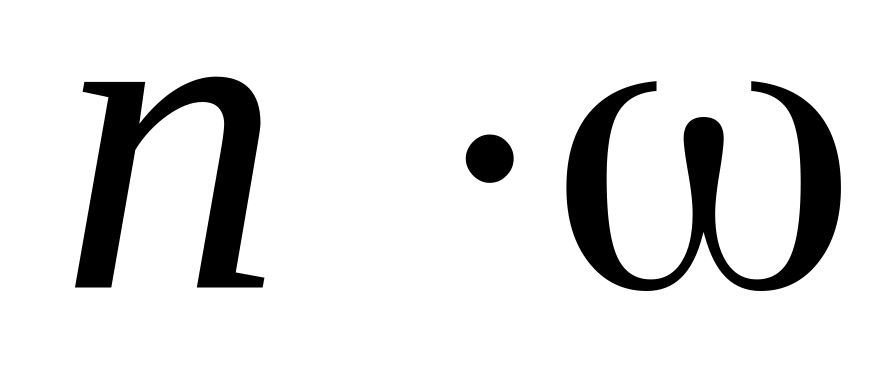, где

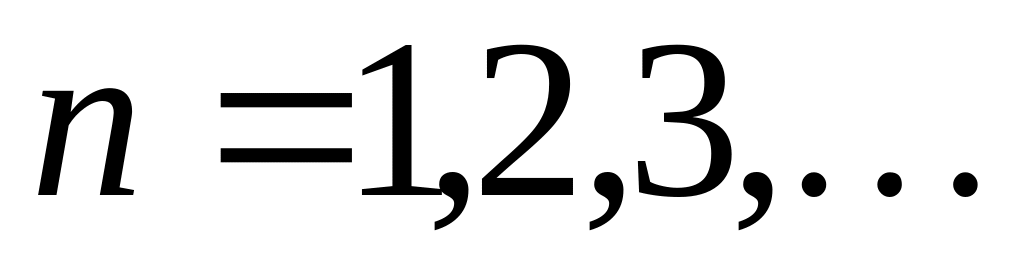
2. Соотношения между амплитудами отдельных гармоник зависят от характера нелинейности, положения исходной рабочей точки на характеристике, а также от амплитуды возбуждающего колебания.