6. 3 Анализ нелинейных цепей по постоянному току

Задачу анализа нелинейных цепей по постоянному току можно сформулировать следующим образом. Задана схема электрической цепи, известны напряжения и токи источников энергии и ВАХ резистивных элементов, требуется определить напряжения и токи ветвей.

Аналитическое решение задачи анализа нелинейных цепей возможно только в случаях простейших цепей. Для практических расчетов широко применяются графические и численные методы анализа.

6. 3. 1 Графический метод

Реализацию графического метода расчета нелинейных цепей рассмотрим на примере простейших соединений нелинейных элементов.

На рисунке 6. 5, а показано последовательное соединение двух нелинейных элементов и , вольт-амперные характеристики которых и заданы (рисунок 6. 5, б). Требуется определить ток I^* и напряжения и на элементах при заданном напряжении на зажимах цепи U=E.

Для вычисления искомых величин построим вспомогательную характеристику: зависимость тока в цепи от суммарного напряжения . При построении этой характеристики производим суммирование напряжений U₁ и U₂ при фиксированных значениях тока I. Построив вспомогательную характеристику , откладываем на оси абсцисс напряжение U=E (точка а на рисунке 6. 5, б), из полученной точки проводим перпендикуляр до пересечения с кривой . Отрезок ab в некотором масштабе m₁ равен искомому току I^*. Из точки b проведем прямую, параллельную оси абсцисс. Отрезки cd и cf в масштабе m_U равны напряжениям и .

а)

б)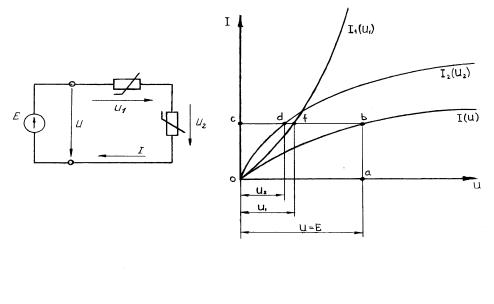

Рисунок 6. 5

Параллельное соединение нелинейных элементов r₁ (I) , r₂ (I) и их вольт-амперные характеристики , представлены на рисунке 6. 6.

а)

б)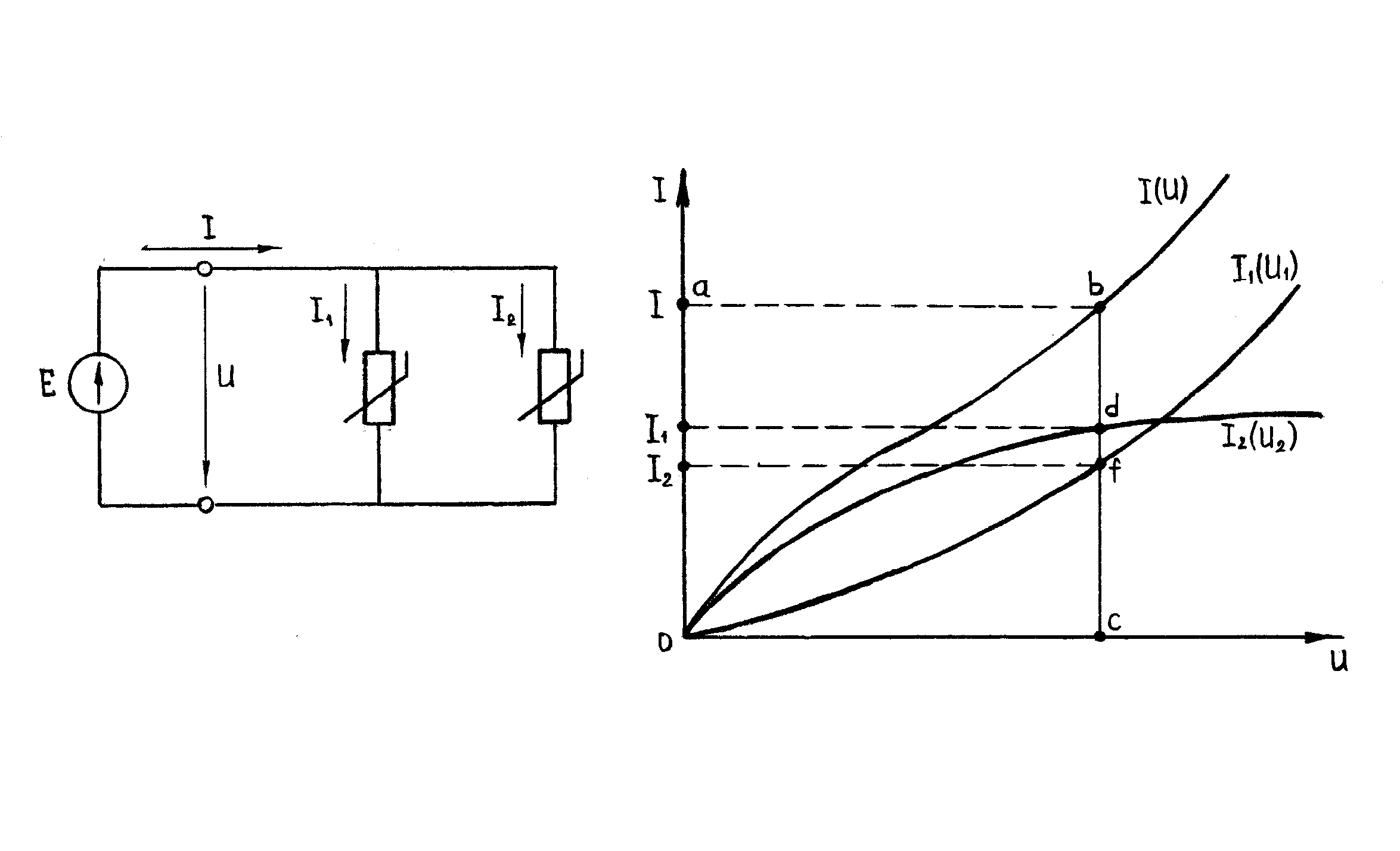

Рисунок 6. 6

Если напряжение, приложенное к цепи, известно, то анализ цепи сводится к определению токов и из ВАХ нелинейных элементов, а ток в неразветвленной части цепи I находится суммированием токов , . Большой интерес представляет случай, когда ток в неразветвленной части цепи задан I= J и необходимо найти напряжения на элементах и токи нелинейных резисторов . При такой постановке задачи необходимо строить вспомогательную характеристику , для чего производится суммирование ординат кривых при одних и тех же значениях напряжений. Затем, отложив по оси ординат отрезок, равный в масштабе току J (точка а на рисунке 9. 6, б), и проведя в полученной точке перпендикуляр до пересечения с характеристикой , находим отрезок ab, который в соответствующем масштабе будет равен напряжению U^* . На пересечении перпендикуляра, опущенного из точки b на ось абсцисс, с характеристиками и получаем точки f и d . По построению отрезки cf и cd в масштабе будут соответствовать токам и .

Графический метод можно использовать для расчета цепей со смешанным соединением нелинейных и линейных элементов. Последовательность графических построений и методика определения токов и напряжений подобна рассмотренным выше примерам.

Графические методы анализа вследствие своей трудоемкости и невысокой точности применяются для сравнительно простых цепей, содержащих один-два нелинейных элемента.