6. 2 Аппроксимация нелинейных характеристик
Как отмечалось в предыдущем разделе, аналитическая форма представления статических характеристик нелинейных элементов является наиболее удобной для практического использования. Для получения аналитического описания характеристик используется, как правило, один из двух подходов. Первый предполагает выполнение анализа физических процессов, имеющих место в рассматриваемом элементе, составление уравнений, описывающих эти процессы, и затем поиск аналитического выражения для статической характеристики путем решения составленных уравнений. Достоинством такого подхода является то, что получаемые соотношения характеризуются параметрами, имеющими конкретный физический смысл. Однако данному подходу присущи и существенные недостатки. Во-первых, необходима достаточно достоверная информация о физических процессах, протекающих в элементе. Во-вторых, уравнения, описывающие внутренние процессы в реальных элементах, как правило достаточно сложны, аналитическое решение их возможно только при введение значительных упрощающих допущений. В результате полученное аналитическое выражение может в весьма малой степени отражать реальную статическую характеристику.
Второй подход основан на аппроксимации характеристик нелинейных элементов, найденных экспериментальным путем.
Режимы работы элементов могут быть различными. В одних режимах токи и напряжения элемента изменяются только в небольшой окрестности некоторой точки покоя, в других режимах область изменения токов и напряжений охватывает всю характеристику или большую ее часть. В соответствии с этим аппроксимирующая эту характеристику функция должна с наибольшей точностью воспроизводить рабочий участок. Чем меньше рабочий участок кривой, тем более простой может быть выбрана функция, аппроксимирующая этот участок характеристики.
Существуют различные способы аппроксимации:
1) линейная;
2) нелинейная;
3) кусочно-линейная;
4) кусочно-нелинейная.
Линейная аппроксимация используется при работе нелинейного элемента в режиме малого сигнала. Аппроксимация нелинейной функции в этом случае осуществляется, как правило, касательной, проведенной или рассчитанной в точке характеристики, в окрестности которой происходят изменения токов и напряжений. В случае нелинейного резистивного двухполюсника такую аппроксимацию можно интерпретировать как замену при расчете нелинейного сопротивления линейным, числено равным дифференциальному сопротивлению. Достоинством линейной аппроксимации является возможность перехода от анализа нелинейной цепи к анализу линейной (линеаризованной) цепи, который является значительно проще. Недостаток- точность такой аппроксимации низкая и даже в режиме малого сигнала погрешность расчета может быть значительной.
При нелинейной аппроксимации используются чаще всего различные степенные ряды.
Предположим, что
к нелинейному двухполюснику приложено
некоторое постоянное воздействие
,
которое определяет его исходный рабочий
режим. Это воздействие будем называть
“смещением”. При этом
–– значение функции в исходной точке.
Если исходное воздействие изменить на
некоторую величину
,
то, представляя новое значение функции
в виде ряда Тейлора, получим
(6. 3)
где
- значения производных функции f (x) в
точке
.
Так как
,
то вместо (6. 3) можно записать
.
Последнее
соотношение представляет собой разложение
функции f(x) в ряд Тейлора в окрестности
точки
и является аналитическим описанием
характеристики элемента. Полученная
формула представляет собой степенной
ряд. Чем большее число членов ряда
учитывается, тем точнее будет выражаться
действительная характеристика. Оставляя
в разложении
слагаемых, получаем многочлен
-ой
степени. Таким образом, аппроксимация
характеристик полиномами приводит к
следующим уравнениям:
а) если
,
то
;
(6. 4)
б) если
,
то
.
(6. 5)
Коэффициенты
,
необходимо подбирать таким образом,
чтобы аппроксимирующее уравнение с
приемлемой точностью описывали рабочий
участок характеристики. Чтобы не
усложнять расчеты, количество членов
аппроксимирующих уравнений (6. 4) и (6. 5)
стараются ограничить как можно меньшим
числом.
Наряду со степенными полиномами, для нелинейной аппроксимации могут использоваться и другие виды функций (экспоненциальная, тригонометрическая и т. п.). Преимущества данного подхода к получению аналитического описания нелинейных характеристик, заключается, во-первых, в возможности нахождения сколь угодно точного выражения и, во-вторых, в отсутствии необходимости знаний о принципе действия рассматриваемого элемента. Недостаток - коэффициенты аппроксимирующих выражений не имеют физического смысла, их численные значения невозможно оценивать и корректировать из общих, теоретических положений. Незначительное изменение хода характеристики или рассмотрения аппроксимируемого участка может приводить к существенным изменениям численных значений коэффициентов , .
В практике радиотехнических расчетов широко применяется метод кусочно-линейной аппроксимации. В этом случае характеристика нелинейного элемента заменяется некоторой совокупностью отрезков прямых линий, совпадающей с реальной кривой с удовлетворительной точностью. Пример кусочно-линейной аппроксимации N-образной ВАХ приведен на рисунке 6. 4. Очевидно, что аппроксимирующие соотношения для каждого участка будут различными.
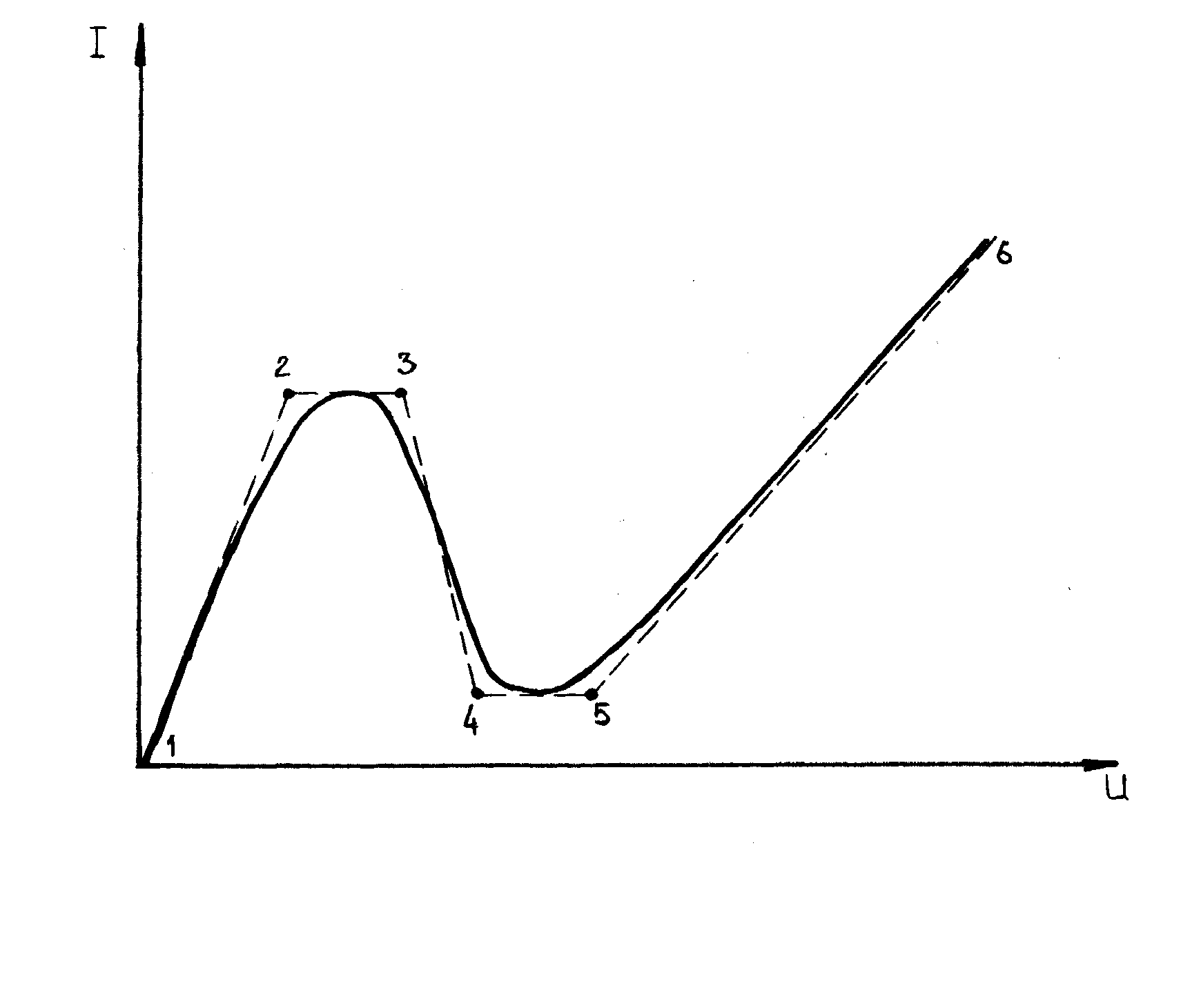
Рисунок 6. 4
Такой метод сохраняя достоинства линейной аппроксимации, позволяет по сравнению с ней значительно повысить точность описания характеристик и, в тоже время, существенно упрощает сам процесс аппроксимации в сравнении с нелинейной аппроксимацией.
Недостатком кусочно-линейной аппроксимации является усложнение алгоритма расчета электрической цепи из-за необходимости постоянного контроля значений переменных. Данная процедура не создает сложностей, если в анализируемой цепи имеется только один элемент, для которого использована кусочно-линейная аппроксимация, но может оказаться чрезмерно трудоемкой с ростом числа таких элементов.
Кусочно-нелинейная аппроксимация используется в случаях, когда ни один из трех рассмотренных методов аппроксимации не дает удовлетворительного результата либо из-за низкой точности, либо из-за сложности полученных соотношений (чрезмерно большое количество членов при аппроксимации степенными полиномами, очень большое количество отрезков при кусочно-линейной аппроксимации). Иногда к кусочно-нелинейной аппроксимации прибегают в случаях, когда в результате анализа физических процессов в элементе получено соотношение, хорошо описывающие значительный участок статической характеристики, но мало приемлемое при каком-либо качественном изменении режима работы нелинейного элемента (например, явление пробоя электронно-дырочного перехода в полупроводниковых приборах). Достаточно часто такая аппроксимация позволяет с требуемой точностью описать характеристику при сравнительно небольшом числе участков, описываемых различными соотношениями (как правило, 2 - 3 участка).