2.2 Метод эквивалентных преобразований цепи
Метод состоит в эквивалентной замене всей электрической цепи или сложных ее частей более простыми по структуре участками. При этом токи и напряжения в непреобразованной части цепи не должны изменяться. Преобразование цепи приводит к значительному упрощению ее расчета.
Замена последовательного соединения резистивных элементов одним эквивалентным. Простейшим видом соединения является последовательное соединение, когда n элементов соединены друг за другом (один вывод предыдущего соединен с одним выводом последующего). В результате получается участок с двумя крайними выводами а и b (двухполюсник), вдоль которого протекает ток, общий для всех элементов (рис.2.6). Напряжение на участке аb при последовательном соединении равно сумме падений напряжений на отдельных элементах:
,
где
— эквивалентное сопротивление
последовательного соединения.
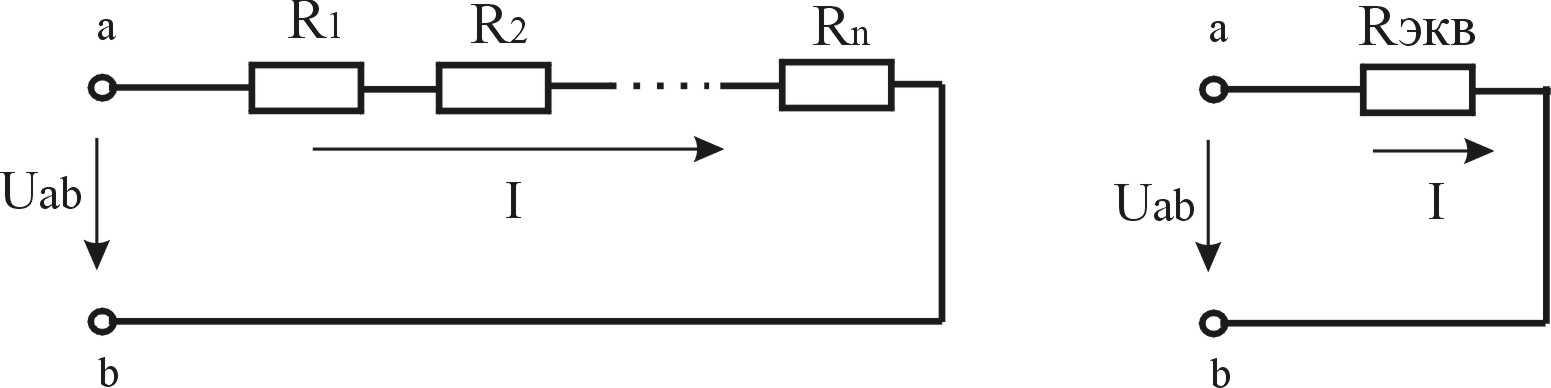
Рисунок 2.6 — Последовательное соединение элементов и его замена
Замена параллельного
соединения резистивных элементов одним
эквивалентным.
При параллельном соединении все п
элементов подключены к одной паре узлов
а
и b,
таким образом общим
для всех элементов является напряжение
,
которое равно разности потенциалов в
узловых точках. Входной ток
распределяется по п
параллельным ветвям, в которых величины
токов определяются по закону Ома
(рис.2.7):
.
Ток
в неразветвленной части цепи определяется
по первому закону Кирхгофа как
.
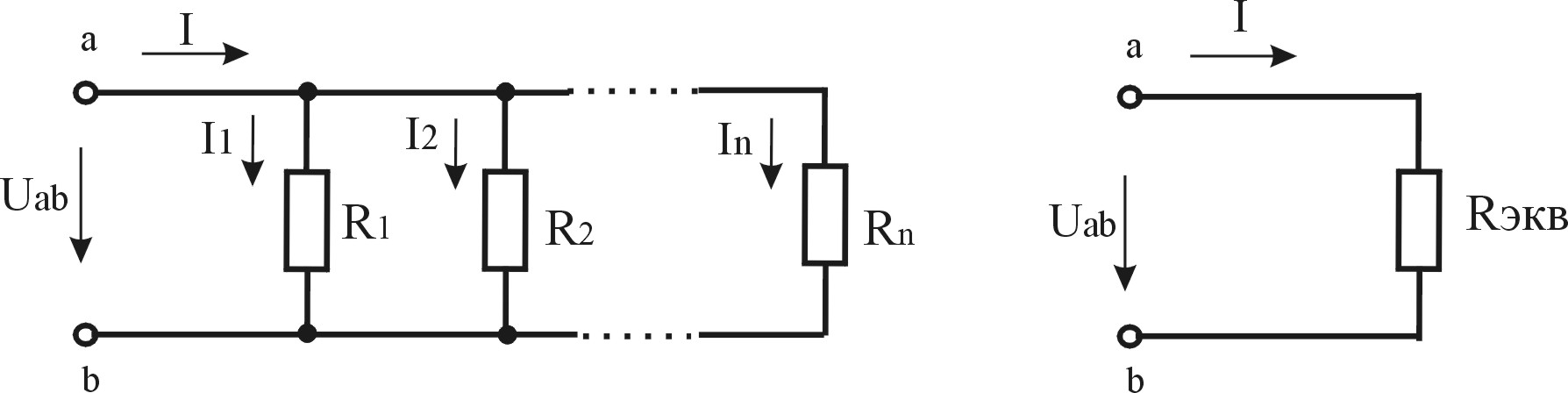
Рисунок 2.7 — Параллельное соединение элементов и его замена
Учитывая условие эквивалентной замены, при подстановке получим :
,
откуда можно определить эквивалентное сопротивление или проводимость параллельного участка цепи:
.
В частном случае при параллельном соединении двух резисторов получаем:
.
Учитывая, что
,
определим по закону Ома токи в ветвях
цепи:
;
.
Полученные соотношения называются формулами разброса.
Взаимная замена цепи резистивных элементов, соединенных треугольником и звездой. В разветвленных цепях встречаются соединения элементов, которые нельзя отнести к последовательному или параллельному соединению. К таким соединениям относится трехлучевая звезда (рис.2.8а) и треугольник (рис.2.8б) сопротивлений. Условием эквивалентной замены является сохранение значений входных токов Іa , Ib , Ic и потенциалов в точках a , b , c .
а б
Рисунок 2.8 — Трехлучевая звезда (а) и треугольник (б) сопротивлений
Формулы преобразования треугольника сопротивлений в эквивалентную звезду:
;
;
.
Формулы преобразования звезды сопротивлений в эквивалентный треугольник:
;
;
.