Дизъюнктор

Дизъюнктор – это простейший логический элемент, выполняющий функцию дизъюнкции двух или более входных сигналов: .

Функция , если хотя бы один из входных сигналов = 1.

Условное графическое обозначение элемента

X₁ 1 y

X₂

Временные диаграммы сигналов на входах и выходах элемента:

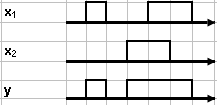
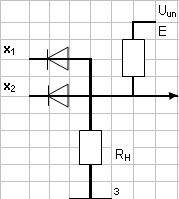
Простейшая реализация элемента ИЛИ – диодная схема:

X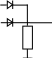 ₁

X₂ y

R_H

З

Схема имеет два или более входов и один выход. Сигнал на выходе возникает при появлении сигнала хотябы на одном из входов. Если на вход подается сигнал положительной полярности Е = 1, соответствующий диод открываеться и через резистор нагрузки проходит ток, падение напряжения от которого снимаеться в виде сигнала бла ≈ Е.

Конъюнктор

Конъюнктор – это простейший логический элемент, выполняющий функцию конъюнкции двух или более входных сигналов:

Выходной сигнал , когда на все входы одновременно воздействуют сигралы «1».

Условное графическое обозначение эл-та:

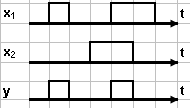
X ₁

X₂ & y

Временные диаграммы сигналов на входах и выходах элемента:

Простейшая реализация элемента И в виде диодной схемы:

Напряжения на выходе U_вых= 1 появиться только тогда, когда все диоды будут заперты, т.е. на всех входах будет потенциал«1». Иначе один из диодов открывается и на нагрузке будет потенциал открытого диода U_вых≈ 0.

Инвертор

Инвертор – простейший логический элемент, выполняющий функцию инверсии входного сигнала .

Условное графическое обозначение элемента: x 1 y

Временные диаграммы входа и выхода сигналов:

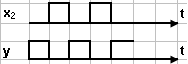
Пример реализации эл-та НЕ с помощью транзисторного ключа:

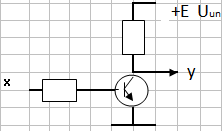
Если сигнал на входе (U_вх≈ 0,5В), то этого напряжения достаточно для полного открытия транзистора, при этом U_вых≈ 0 (Y = 0).

Если , то входное напряжение ключа = 0, транзистор закрыт и U_вых ≈ Е.

Синтез комбинационных схем

1. Переключательная функция проектируемой схемы представляется в СДНФ. Затем находится МДНФ функции.

2. МДНФ функции представляют в виде суперпозиции логических элементов. Если число входов логич. элементов не достаточно для реализации функции по этой форме, то производят группировку переменных в соответствии с числом входов ЛЭ.

3. Состаавляеться комбинационная схема. При этом учитываеться нагрузочная способность элементов.

Минимизация переключательных функций.

Минимизация функции может выполняться аналитическим методом посредством использования законов и тождеств алгебры-логики; или графическим методом при помощи диаграмм Вейча или карт Карно.

Два минтерма (конституента) называют соседними, если в них все термы (буквы), за исключением одной, совпадают. Например: .

Тогда

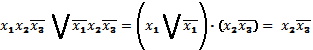
Это называют операцией склеивания или правилом минимизации: дизъюнкцию двух соседних минтермов можно заменить одним контермом, не зависящим от одной переменной.

Если есть 4 минтерма

В общем случае: одним контермом n переменных независящим от m переменных (m <= n), можно заменить дизъюнкцию 2^m минтермов, если каждый из них имеет по m соседних минтермов среди остальных 2^m-1 минтермов.

Т.к. , то склеить можно только 2^m минтермов: 2, 4, 8 и т.д. Один и тот же минтерм может использоваться для склеивания несколько раз в случае если он соседний несоседним между собой минтермам.

Н-р

Для получения МНФ в базисах И-НЕ и ИЛИ-НЕ к СДНФ (СКНФ) применяют законы дуальности (теоремы де Моргана). ;